JUMP TO TOPIC
Types of Triangles – Explanation & Examples
In Geometry, a triangle is the most important shape, defined as a closed two-dimensional diagram containing 3 sides, 3 angles, and 3 vertices. In simple words, a triangle is a polygon with 3 sides. The word triangle is taken from the Latin word ‘triangulus,’ which means three-cornered.
During ancient times, astronomers had created a method called triangulation to determine the distances of the distant stars. They measure the distance from two different locations, then measure the angle created by shift or parallax, formed by the observer’s movement between the two locations. Then they used to apply the law of sines for calculating the required distance.
The Egyptians created the pyramids around 2900 B.C. Its shape is actually that of a 3D pyramid, which has triangular faces. It is a perfectly engineered model that its lengths and angles on all sides are the same. Miletus (624 BC – 547 BC), a Greek mathematician, adopted Egypt’s geometry and was brought to Greece.
Aristarchus (310 BC – 250 BC), a Greek mathematician, used the above method to find the distance between the Earth and the Moon. Eratosthenes (276 BC – 195 BC), again, used the same method to determine the distance around the surface of Earth (called circumference).
This article will discuss the meaning of a triangle, the different types of triangles and their properties, and their real-life applications.
What is a Triangle?
A triangle is a two-dimensional closed figure with 3 sides. It is a polygon with three corners, three vertices, and three angles joined together that forms a closed diagram. We use the symbol ∆ to denote a triangle.
Figures A and B are triangles.
Different Types of Triangles
The types of triangles are classified based on:
- The lengths of their sides
- Interior angles
Classification of triangles according to the measure of interior angles
According to the measure of interior angles, we can classify triangles into three categories:
- Acute-angled
- Obtuse-angled
- Right-angled
Acute triangle
An acute angle triangle is a triangle in which all three interior angles are less than 90 degrees.
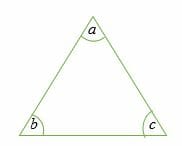
Each one of the angles a, b and c is less than 90 degrees.
Obtuse triangle
An obtuse triangle is a triangle in which one of the interior angles is more than 90 degrees.
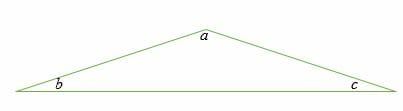
Angle a is more obtuse, while angles b and c are acute.
Right Triangle
A right triangle is a triangle in which one of the angles is exactly 90 degrees. The hypotenuse is the side of a right triangle with the longest length.
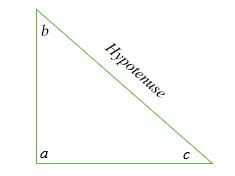
In the illustration above, angle a = 90 degrees while angles b and c are acute angles.
Classification of triangles according to the length of their sides
We can classify triangles into 3 types based on the lengths of their sides:
- Scalene
- Isosceles
- Equilateral
Isosceles triangle
An isosceles triangle is a triangle in which two sides and two angles are equal. Equal lengths of a triangle are shown by making an arc on each side.
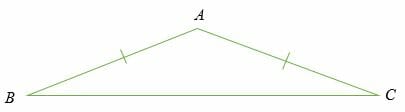
In the diagram above, the length of side AB = AC and ∠ ABC =∠ ACB.
Equilateral triangle
An equilateral triangle has all three sides equal, and all three interior angles equal, too. In this case, each interior angle of an equilateral triangle is 60 degrees. An equilateral triangle is sometimes referred to as an equiangular triangle because all three angles are equal.
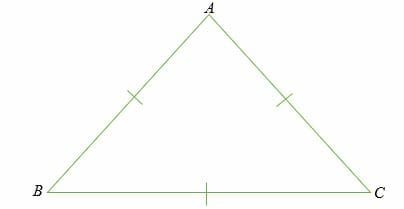
In an equilateral triangle, the sides AB = BC = AC and ∠ ABC =∠ ACB = ∠ BAC
Note that the angles of an equilateral triangle do not depend on the lengths of the sides.
Scalene Triangle
A scalene triangle is a triangle in which all the sides have different measures and all the interior angles are also different.
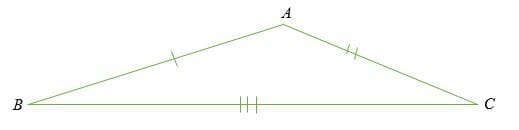
Properties of Triangle
The properties of triangles have a broad use. Many mathematicians used it in solving their problems. Euclidean geometry and trigonometry make great use of the properties of triangles.
Here are a few basic properties of a triangle:
- A triangle is a 2-D polygon
- A triangle has 3 sides, 3 angles, and 3 vertices.
- The sum of lengths of any two sides of a triangle is more than the remaining side’s length.
- The sum of the lengths of the three sides gives the perimeter of triangles.
- The area of a triangle is equal to the product of the base and the height.
Worked examples on different types of triangles
Example 1
Find the value of angle x in the triangle below.
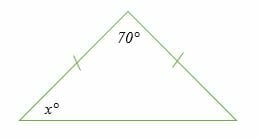
Solution
This is an isosceles triangle in which two sides are equal, and also two angles are equal. Therefore,
x = (180° – 70°)/2
x = 110°/2
= 55°
Example 2
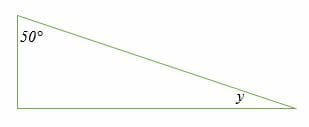
Find angle y in the right triangle shown below.
Solution
One angle of a right triangle is equal to 90°. So, we;
y + 50 + 90 = 180
y = (180 – 140) °
y = 40°
Example 3
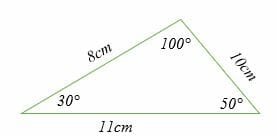
Classify the following triangle.
Solution
This is a scalene triangle because all the sides and angles have different measurements. Similarly, the triangle can also be classified as an obtuse triangle because one angle is obtuse.
Example 4
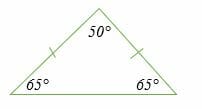
Classify the triangle shown below.
Solution
This is an isosceles triangle. Two sides are equal, and two angles are equal in measurement.
Applications of Triangles
Let’s explore some of the real-life applications of triangles:
- Traffic Signs: Most of the traffic signs are displayed on triangular structures.
- The Pyramids of Egypt: Pyramids are ancient monuments constructed by Egyptians. Pyramids are triangular in shape.
- Truss: The trusses of roofs or bridges are fabricated in a triangular shape because a triangle is considered the strongest shape.
- The Bermuda Triangle: The Bermuda Triangle is a triangular area in the Atlantic Ocean where it is believed that any ship or aircraft that passes at the point is swallowed. 50 ships and 20 air crafts are believed to have been mysteriously disappeared at the Bermuda Triangle.
- Global Positioning System (GPS) works on triangulation algorithms to determine an object’s longitude and latitude.
- A ladder leaning against a wall makes the shape of a triangle.
- The Eiffel Tower is triangular in shape.
- The triangles concept calculates the height or altitude of tall objects such as flag posts, mountains, buildings, etc.
- Sandwiches and pizza slices are triangular-shaped.
