What Is 12.5 Percent of 40 + Solution with Free Steps?
The 12.5 percent of 40 is equal to 5. It can be easily calculated by dividing 12.5 by 100 and multiplying the answer with 40 to get 5. The easiest way to get this answer is by solving a simple mathematical problem of percentage. You need to find 12.5% of 40 for some sale or real-life problem. Divide 12.5 by 100, multiply the answer with 40, and get the 12.5% of 40 value in seconds.This article will explain the full process of finding any percentage value from any given quantity or number with easy and simple steps.
The easiest way to get this answer is by solving a simple mathematical problem of percentage. You need to find 12.5% of 40 for some sale or real-life problem. Divide 12.5 by 100, multiply the answer with 40, and get the 12.5% of 40 value in seconds.This article will explain the full process of finding any percentage value from any given quantity or number with easy and simple steps.
What Is 12.5 percent of 40?
The 12.5 percent of 40 is 5.The percentage can be understood with a simple explanation. Take 40, and divide it into 100 equal parts. The 12.5 number of parts from the total 100 parts is called 12.5 percent, which is 5 in this example.How To Calculate 12.5 percent of 40?
You can find 12.5 percent of 40 by some simple mathematical steps explained below.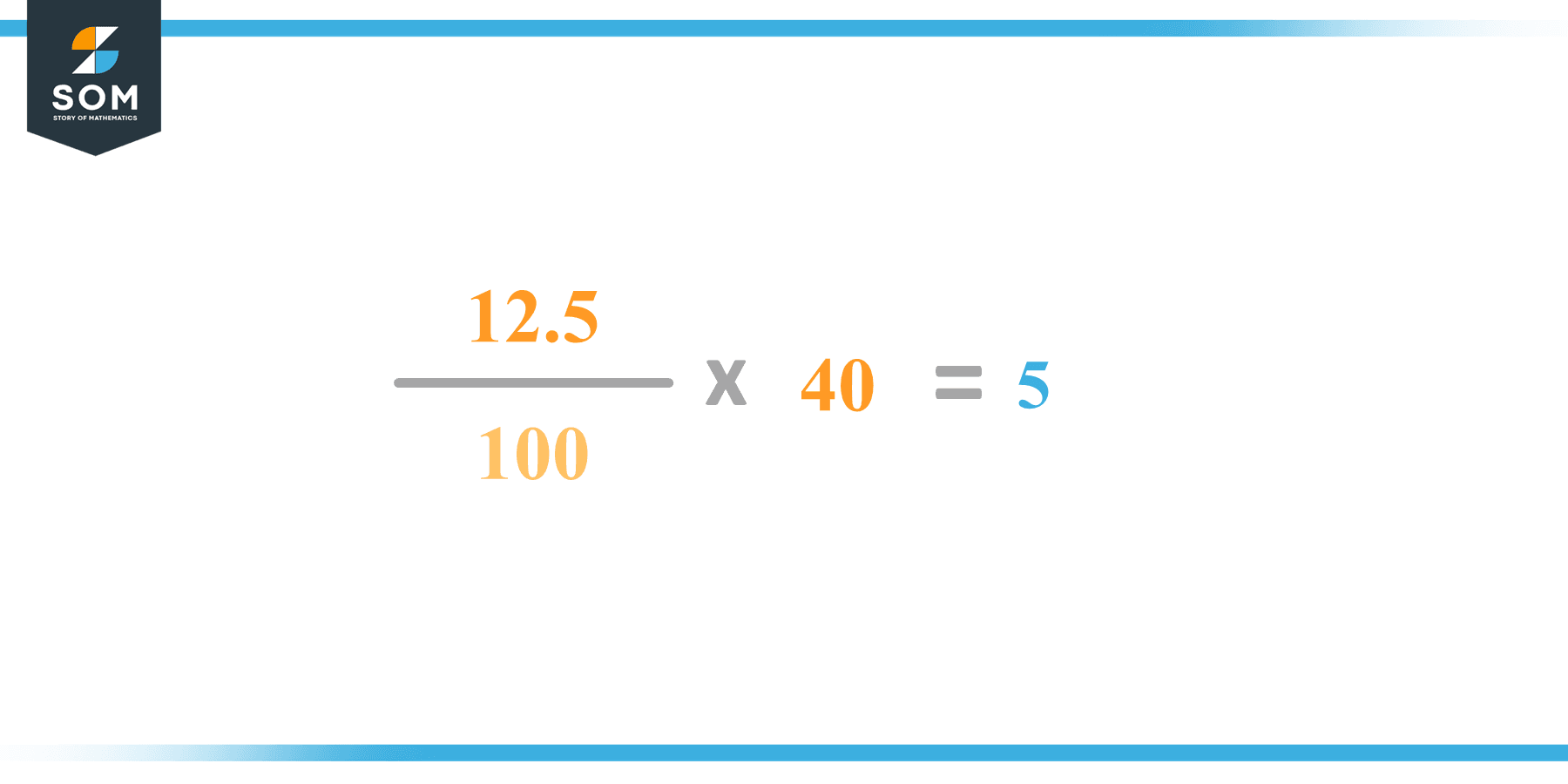
Step 1
Firstly, depict 12.5 percent of 40 as a fractional multiple as shown below:12.5% x 40
Step 2
The percentage sign % means percent, equivalent to the fraction of 1/100.Substituting this value in the above formula:= (12.5/100) x 40
Step 3
Using the algebraic simplification process, we can arithmetically manipulate the above equation as follows:= (12.5 x 40) / 100
= 500 / 100
= 5
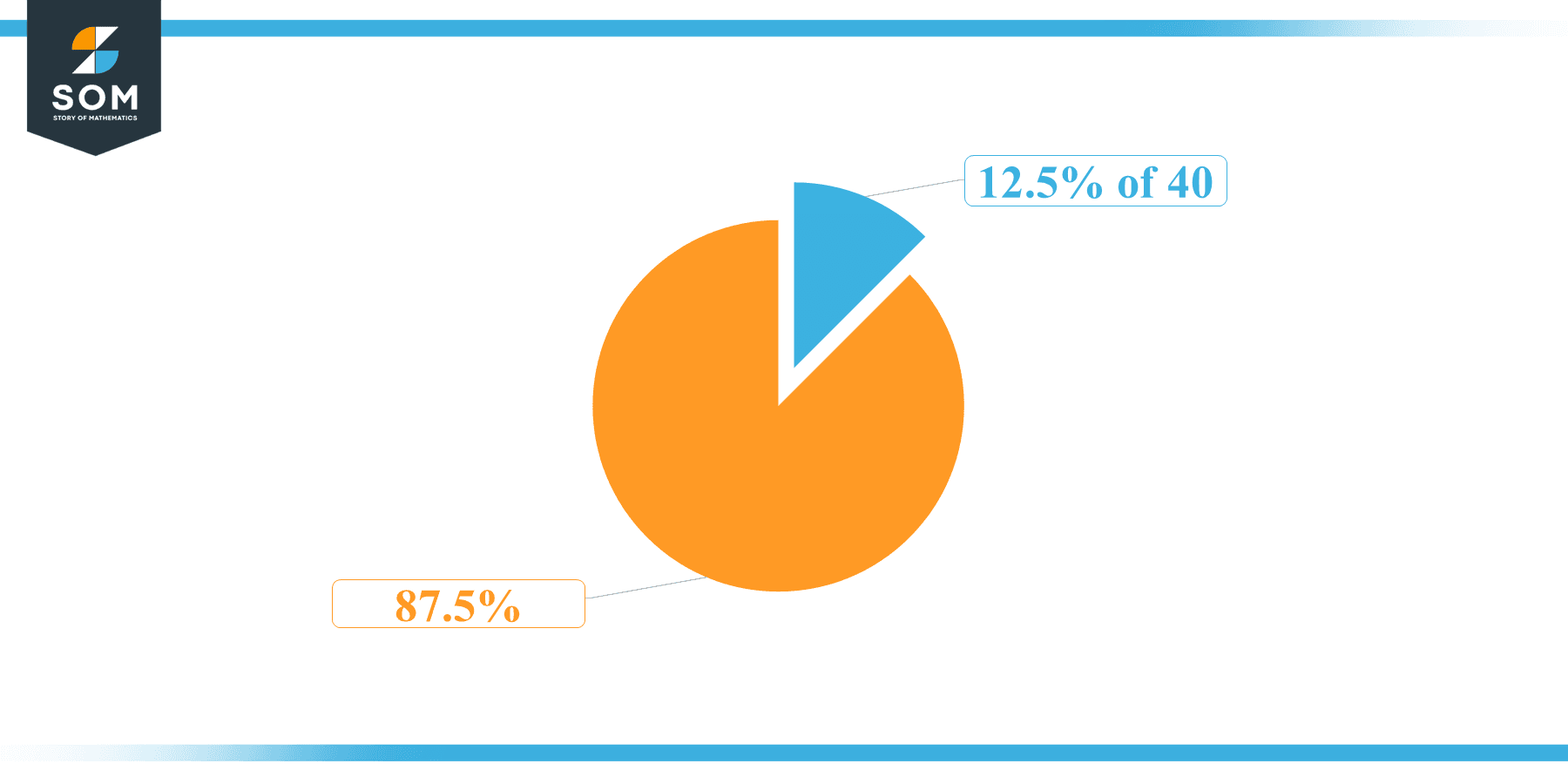 This percentage can be represented on a pie chart for visualization. Let us suppose that the whole pie chart represents the 40 value. Now, we find 12.5 percent of 40, which is 5. The area occupied by the 5 value will represent the 12.5 percent of the total 40 value. The remaining region of the pie chart will represent 87.5 percent of the total 40 value. The 100% of 40 will cover the whole pie chart as 40 is the total value.Any given number or quantity can be represented in percentages to better understand the total quantity. The percentage can be considered a quantity that divides any number into hundred equal parts for better representation of large numbers and understanding.Percentage scaling or normalization is a very simple and convenient method of representing numbers in relative terms. Such notations find wide application in many industrial sectors where the relative proportions are used.
This percentage can be represented on a pie chart for visualization. Let us suppose that the whole pie chart represents the 40 value. Now, we find 12.5 percent of 40, which is 5. The area occupied by the 5 value will represent the 12.5 percent of the total 40 value. The remaining region of the pie chart will represent 87.5 percent of the total 40 value. The 100% of 40 will cover the whole pie chart as 40 is the total value.Any given number or quantity can be represented in percentages to better understand the total quantity. The percentage can be considered a quantity that divides any number into hundred equal parts for better representation of large numbers and understanding.Percentage scaling or normalization is a very simple and convenient method of representing numbers in relative terms. Such notations find wide application in many industrial sectors where the relative proportions are used.