All About Yang Hui – A Nobel Chinese Mathematician

Way back in math history, Yang Hui happens to be a reputable figure, one who was known for his remarkable contributions in the field of mathematics. He was a great Chinese mathematician and writer.

He served through his inventions during the Song dynasty in China. So, the question is, what did he contribute to the field of mathematics? And how has his contribution influenced the world at large? Well, you will get to know more about this as you read on.

Biography

This notable Chinese mathematician was born in 1238 AD in Hang Prefecture, China. He was officially addressed as Qianguang and was a mandarin. The most significant part of his contribution that stands him out from others emerged from the remarkable recognition of his mathematical works gains in today’s world; his work is considered as a masterpiece. During his lifetime, He had the privilege of being under the tutorage of Liu I, who was a native of Chung-shan.

Yang’s notable works/contributions include magic squares, magic circles, and the binomial theorem. In China, mathematics emerged independently in the 11th century BC.

At that time, the country developed a real number system that covers both large and negative numbers, more than one numeral system (base 2 and base 10), algebra, geometry, number theory, and trigonometry.

Mathematical Contributions

The invention of Hui’s Triangle is one of his mind-blowing contributions. His works are mentioned in the Wenyan ge Shumu (Catalogue of the Books of the Ming Imperial Library, 1441). 

Ruan Yuan, who was also a reputable Chinese mathematician, found the fragments of Yang’s work “Xiangjie jiuzhang suanfa” (A Detailed Analysis of the Nine Chapters on the Mathematical Procedures, 1261) in a handwritten copy of a majestic Ming dynasty encyclopedia. Later, he discovered an edition of Yang Hui suanfa, which was also referred to as Yang Hui’s Mathematical Methods, 1275) in Suzhou, and that was when he started the magic circles, magic squares, and the binomial theorem.

His books are part of the few modern Chinese mathematics works that are sustained till-date. Though he authored a couple of books but had only two of his publications to limelight, these are; the “Xugu Zhaiqi” and the “Suanfa Tongbian Benmo.”

Yang Hui’s Triangle

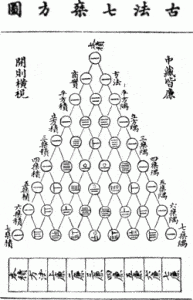Triangles of Yang Hui

The Triangle is a prestigious invention for most mathematical work that deals with the operation of prime numbers.  

The Triangle shared incredible similarities with Pascal’s Triangle, which was discovered by his predecessor named Jia Xian.

Pascal’s Triangle

The earliest existing Chinese illustration of ‘Pascal’s Triangle’ was from Yang’s book Xiangjie

Jiuzhang Suanfa of 1261 AD. This writing was a compilation of the problems from the Han dynasty classic and its reviews. Jiuzhang Suanshu (Nine Chapters on the Mathematical Procedures) was also one of his famous writings; it contains the oldest description of the Chinese Triangle, known as Blaise Pascal’s Triangle in the Western world.

“Yang Hui’s Triangle” was introduced by Jia Xian, a Chinese mathematician who set it forth about 500 years before Blaise Pascal. Yang Hui’s Triangle is a special triangular arrangement of numbers that is used today in most mathematical works. In Europe, this Triangle is often named after Blaise Pascal, who was a French mathematician in the 17th Century.

Before Hui’s discovery, this triangular arrangement of numbers was described by Arabian, who was a poet and mathematician in Omar Khayyam and the Indian mathematician Halayudha in 975. All of these contributions, renovations, and suggestions from different historic mathematicians constituted to the uniqueness of the Chinese Triangle. Below is a glimpse of what the Triangle looks like:

At the top of the Triangle, there is an 11, which makes up the 0th row. The 1st row  contains two 11s each formed by adding the two numbers above them, one to the left and one to the right, 0 and 11. (All numbers outside the Triangle are 0s.)

You can do the same to create the 2^nd row;  and all the subsequent rows.  is a number in the Triangle and can be found by using where is the number of the row and is the number of the element in that row.

This is important when solving a particular term in the expansion of binomial, in the form of

In a book, Rújī Shìsuǒ (Piling-up Powers and Unlocking Coefficients) Jia described the method as ‘li cheng shi suo’ which explains the tabulation of a number system used to unlock binomial coefficients. This method appeared again in the publication of Zhu Shijie’s book “Jade Mirror of the Four Unknowns of 1303 AD”.

Publications

Hui finally had two published mathematical books, which was published around 1275 AD. At that time, the books were titled Xugu Zhaiqi Suanfa and Suanfa Tongbian Benmo. In his previous book, he wrote about the arrangement of natural numbers around concentric and nonconcentric circles, which were known as magic circles and magic squares, providing rules for their construction.

In his work, he criticized the earlier works of Li Chunfeng and Liu Yi. He said, “the men of the old era had changed the name of their methods vary from problem to problem since no specific explanation was given, there is no way of telling their theoretical source.”

Yang’s Writings

In his writings, he provided theoretical proof for the complements of the parallelograms. He shared a common idea with Euclid’s, a Greek mathematician in the 300 BC. Yang used the case of a rectangle and gnomon. He represented the quadratic equations with negative coefficients of.’ With an exceptional ability to manipulate decimal fractions and obtain consistent results from it. One of his writings, “Mathematical Methods” was compiled with a profound mathematical perspective.

At the beginning of his book, he shared some practical guides in the approach of mathematics. This guide was originated from the multiplication table, called in the Chinese tradition, and then the study of positions for the layout of numerals and the multiplication algorithms for higher numbers. In his compilation, he also described a geometric method on how to solve quadratic equations in detail.

A variety of magic squares can be found in “Strange Mathematical Methods,” which includes a  square such that each vertical and horizontal line of numbers adds to 505. Over the preceding years, he produced lots of material to support his concept. Still, he published nothing more until 1274 when Cheng Chu Tong Bian Ben Mo, which means Alpha and omega of variations on multiplication and division, was developed.

Chinese Mathematicians

The 13th Century was possibly the most notable mathematical period in the history of China. In 1450, Wu ching, who was the Ming mathematician, wrote the Chiu–chang

Hsiang–chu pi–lei suan–fa which was a Comparative Detailed Analysis of the Mathematical Rules in the Nine Chapters.

In his writing, Chieh explained that Wu Ching’s “old questions” were based on Yang Hui’s Hsiang–Chieh Chiu chang suan–fa. A large volume of I–chia–t’ang ts’ ung–shu edition of the book has been translated into English by Lam Lay Youg, who was a professor at the University of Singapore.

His role as a Chinese Mathematician

Yang Hui published some of his other mathematical works, “Jih–Yung Suan–fa“ (“Mathematical Rules in Common Use”), in 1262. It was based on two volumes. Although the book is gone out of sales. However, some of its sections were retrieved and restored by Li Yen from the Chia Suan–fa in the Yujng–lo ta–tien encyclopedia. This book seems to be quite introductory due to the information shared.

The book “Hsiang–Chieh Chiu–change suan–fa“ was possibly known as one of the best sold in his time.

In the book, he has explained the questions and provided answers in Chiu–chang suanshu, illustrating each with a diagram. He gave detailed solutions for all arithmetic problems. He made comparisons between Problems of the same nature. In the last chapter of T suan lei, Yang Hui, reclassified all the 246 problems in the Chiu–chang suanshu for the benefit of other mathematical students.

Chinese Triangle

The parts restored from the Yung–lo ta–tien encyclopedia contained the most advanced illustration of the “Chinese triangle.” Hui stated that this diagram was derived from an earlier mathematical text, known as the Shih–so Suan–Shu Chia Hsien. This diagram shows the coefficients of the expansion of n up to the sixth power.

A different diagram that shows the coefficients up to the eighth power was found later in the early 14^th –century, a work of Ssu–yiian yϋ–cheien of Chu Shih–Chieh. Other Chinese mathematicians who used the Pascal triangle before Blaise Pascal were Wu Ching (1450), Chou Shu–hsϋeh (1588), and Ch’eng Tawie (1592). Yang Hui’s first publication is a study on Liu Hui’s Chiu–chang suan–shu. This publication is still official in China, and it has been for more than 1,000 years now.

Achievements of Yang Hui

The math icon has indeed achieved and accomplished a lot in his time. All of his works were practical explanations of the importance and origin of Chinese Mathematics. His Chinese Triangle has been a famous yet useful Chinese mathematical invention of all time that is used and acknowledge in the world at large.

Hui’s biography records exploits, inventions, and contributions to China in the world of mathematics; it’s no doubt that the icon was a guru in his time. As a hero, he left behind a considerable number of writings that made him stand out from other mathematicians. All of his works and contributions reflected his interest in the field of mathematics. He covered a comprehensive range than any of his contemporaries.

This prestigious Chinese mathematician had not left anything related to his personal life; instead, all he had was his writings and services in the field of mathematics. His work is still a source of inspiration and a light on the path of most modern mathematicians. The Chinese Triangle has been one of his notable accomplishments.

Today, the Triangle is used in the western world and is popularly known as the Pascal Triangle. I bet you know the Pascal Triangle, that one of his inventions, and it is widely used across the globe.