GEORGE BOOLE – INVENTOR OF BOOLEAN LOGIC
Biography
|
George Boole (1815-1864) |
The British mathematician and philosopher George Boole, along with his near contemporary and countryman Augustus de Morgan, was one of the few since Leibniz to give any serious thought to logic and its mathematical implications. Unlike Leibniz, though, Boole came to see logic as principally a discipline of mathematics, rather than of philosophy.
His extraordinary mathematical talents did not manifest themselves in early life. He received his early lessons in mathematics from his father, a tradesman with an amateur interest in in mathematics and logic, but his favourite subject at school was classics. He was a quiet, serious and modest young man from a humble working class background, and largely self-taught in his mathematics (he would borrow mathematical journals from his local Mechanics Institute).
It was only at university and afterwards that his mathematical skills began to be fully realized, although, even then, he was all but unknown in his own time, other than for a few insightful but rather abstruse papers on differential equations and the calculus of finite differences. By the age of 34, though, he was well respected enough in his field to be appointed as the first professor of mathematics of Queen’s College (now University College) in Cork, Ireland.
But it was his contributions to the algebra of logic which were later to be viewed as immensely important and influential. Boole began to see the possibilities for applying his algebra to the solution of logical problems, and he pointed out a deep analogy between the symbols of algebra and those that can be made to represent logical forms and syllogisms. In fact, his ambitions stretched to a desire to devise and develop a system of algebraic logic that would systematically define and model the function of the human brain. His novel views of logical method were due to his profound confidence in symbolic reasoning, and he speculated on what he called a “calculus of reason” during the 1840s and 1850s.
Boolean Logic
|
Boolean logic |
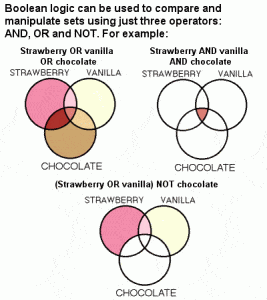
Determined to find a way to encode logical arguments into a language that could be manipulated and solved mathematically, he came up with a type of linguistic algebra, now known as Boolean algebra. The three most basic operations of this algebra were AND, OR and NOT, which Boole saw as the only operations necessary to perform comparisons of sets of things, as well as basic mathematical functions.
Boole’s use of symbols and connectives allowed for the simplification of logical expressions, including such important algebraic identities as: (Xor Y) = (Yor X); not(not X) = X; not(Xand Y) = (not X) or (not Y); etc.
He also developed a novel approach based on a binary system, processing only two objects (“yes-no”, “true-false”, “on-off”, “zero-one”). Therefore, if “true” is represented by 1 and “false” is represented by 0, and two propositions are both true, then it is possible under Boolean algebra for 1 + 1 to equal 1 ( the “+” is an alternative representation of the OR operator)
Despite the standing he had won in the academic community by that time, Boole’s revolutionary ideas were largely criticized or just ignored, until the American logician Charles Sanders Peirce (among others) explained and elaborated on them some years after Boole’s death in 1864.
Almost seventy years later, Claude Shannon made a major breakthrough in realizing that Boole’s work could form the basis of mechanisms and processes in the real world, and particularly that electromechanical relay circuits could be used to solve Boolean algebra problems. The use of electrical switches to process logic is the basic concept that underlies all modern electronic digital computers, and so Boole is regarded in hindsight as a founder of the field of computer science, and his work led to the development of applications he could never have imagined.
<< Back to Riemann | Forward to Cantor >> |