JUMP TO TOPIC
BERNHARD RIEMANN – THE NOTORIOUS GERMAN MATHEMATICIAN
Biography
 |
Bernhard Riemann (1826-1866) |
Bernhard Riemann was another mathematical giant hailing from northern Germany. Poor, shy, sickly and devoutly religious, the young Riemann constantly amazed his teachers and exhibited exceptional mathematical skills (such as fantastic mental calculation abilities) from an early age, but suffered from timidity and a fear of speaking in public. He was, however, given free rein of the school library by an astute teacher, where he devoured mathematical texts by Legendre and others, and gradually groomed himself into an excellent mathematician. He also continued to study the Bible intensively, and at one point even tried to prove mathematically the correctness of the Book of Genesis.
Although he started studying philology and theology in order to become a priest and help with his family’s finances, Riemann’s father eventually managed to gather enough money to send him to study mathematics at the renowned University of Göttingen in 1846, where he first met, and attended the lectures of, Carl Friedrich Gauss. Indeed, he was one of the very few who benefited from the support and patronage of Gauss, and he gradually worked his way up the University’s hierarchy to become a professor and, eventually, head of the mathematics department at Göttingen.
Riemannian Geometry, also called Elliptic Geometry
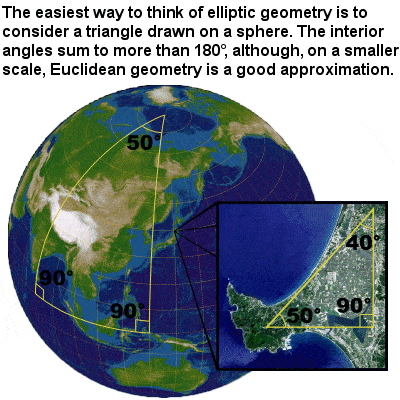 |
Elliptic geometry |
Riemann developed a type of non-Euclidean geometry, different to the hyperbolic geometry of Bolyai and Lobachevsky, which has come to be known as elliptic geometry. As with hyperbolic geometry, there is no such thing as parallel lines, and the angles of a triangle do not sum to 180° (in this case, however, they sum to more than 180º). He went on to develop Riemannian geometry, which unified and vastly generalized the three types of geometry, as well as the concept of a manifold or mathematical space, which generalized the ideas of curves and surfaces.
A turning point in his career occurred in 1852 when, at the age of 26, have gave a lecture on the foundations of geometry and outlined his vision of a mathematics of many different kinds of space, only one of which was the flat, Euclidean space which we appear to inhabit. He also introduced one-dimensional complex manifolds known as Riemann surfaces. Although it was not widely understood at the time, Riemann’s mathematics changed how we look at the world, and opened the way to higher dimensional geometry, a potential which had existed, unrealized, since the time of Descartes.
Metric
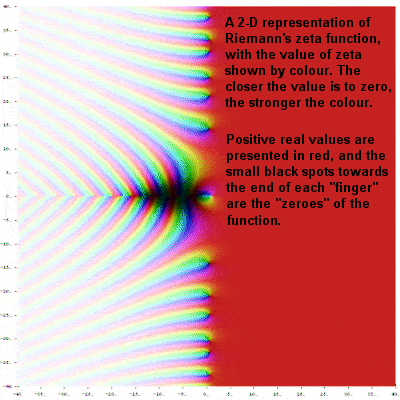 |
2-D representation of Riemann’s zeta function |
With his “Riemann metric”, Riemann completely broke away from all the limitations of 2 and 3 dimensional geometry, even the geometry of curved spaces of Bolyai and Lobachevsky, and began to think in higher dimensions, extending the differential geometry of surfaces into n dimensions. His conception of multi-dimensional space (known as Riemannian space or Riemannian manifold or simply “hyperspace”) enabled the later development of general relativity, and is at the heart of much of today’s mathematics, in geometry, number theory and other branches of mathematics.
A Tensor
He introduced a collection of numbers (known as a tensor) at every point in space, which would describe how much it was bent or curved. For instance, in four spatial dimensions, a collection of ten numbers is needed at each point to describe the properties of the mathematical space or manifold, no matter how distorted it may be.
Zeta Function
Riemann’s big breakthrough occurred while working on a function in the complex plane called the Riemann zeta function (an extension of the simpler zeta function first explored by Euler in the previous century). He realized that he could use it to build a kind of 3-dimensional landscape, and furthermore that the contours of that imaginary landscape might be able to unlock the Holy Grail of mathematics, the age-old secret of prime numbers.
 |
3-D representation of Riemann’s zeta function and Riemann’s Hypothesis |
Riemann noticed that, at key places, the surface of his 3-dimensional graph dipped down to height zero (known simply as “the zeroes”) and was able to show that at least the first ten zeroes inexplicably appeared to line up in a straight line through the 3-dimensional landscape of the zeta-function, known as the critical line, where the real part of the value is equal to ½.
With a huge imaginative leap, Riemann realized that these zeroes had a completely unexpected connection with the way the prime numbers are distributed. It began to seem that they could be used to correct Gauss’ inspired guesswork regarding the number of primes as numbers as one counts higher and higher.
Riemann Hypothesis
The famous Riemann Hypothesis, which remains unproven, suggests that ALL the zeroes would be on the same straight line. Although he never provided a definitive proof of this hypothesis, Riemann’s work did at least show that the 15-year-old Gauss’ initial approximations of the incidence of prime numbers were perhaps more accurate than even he could have known, and that the primes were in fact distributed over the universe of numbers in a regular, balanced and beautiful way.
The discovery of the Riemann zeta function and the relationship of its zeroes to the prime numbers brought Riemann instant fame when it was published in 1859. He too, though, died young at just 39 years of age, in 1866, and many of his loose papers were accidentally destroyed after his death, so we will never know just how close he was to proving his own hypothesis. Over 150 years later, the Riemann Hypothesis is still considered one of the fundamental questions of number theory, and indeed of all mathematics, and a prize of $1 million has been offered for the final solution.
<< Back to Bolyai and Lobachevsky | Forward to Boole >> |
