PYTHAGORAS OF SAMOS
 |
Pythagoras of Samos (c.570-495 BCE) |
Biography – Who was Pythagoras
It is sometimes claimed that we owe pure mathematics to Pythagoras, and he is often called the first “true” mathematician. But, although his contribution was clearly important, he nevertheless remains a controversial figure.
He left no mathematical writings himself, and much of what we know about Pythagorean thought comes to us from the writings of Philolaus and other later Pythagorean scholars. Indeed, it is by no means clear whether many (or indeed any) of the theorems ascribed to him were in fact solved by Pythagoras personally or by his followers.
The school he established at Croton in southern Italy around 530 BCE was the nucleus of a rather bizarre Pythagorean sect. Although Pythagorean thought was largely dominated by mathematics, it was also profoundly mystical, and Pythagoras imposed his quasi-religious philosophies, strict vegetarianism, communal living, secret rites and odd rules on all the members of his school (including bizarre and apparently random edicts about never urinating towards the sun, never marrying a woman who wears gold jewellery, never passing an ass lying in the street, never eating or even touching black fava beans, etc) .
The members were divided into the “mathematikoi” (or “learners“), who extended and developed the more mathematical and scientific work that Pythagoras himself began, and the “akousmatikoi” (or “listeners“), who focused on the more religious and ritualistic aspects of his teachings. There was always a certain amount of friction between the two groups and eventually the sect became caught up in some fierce local fighting and ultimately dispersed. Resentment built up against the secrecy and exclusiveness of the Pythagoreans and, in 460 BCE, all their meeting places were burned and destroyed, with at least 50 members killed in Croton alone.
The over-riding dictum of Pythagoras’s school was “All is number” or “God is number”, and the Pythagoreans effectively practised a kind of numerology or number-worship, and considered each number to have its own character and meaning. For example, the number one was the generator of all numbers; two represented opinion; three, harmony; four, justice; five, marriage; six, creation; seven, the seven planets or “wandering stars”; etc. Odd numbers were thought of as female and even numbers as male.
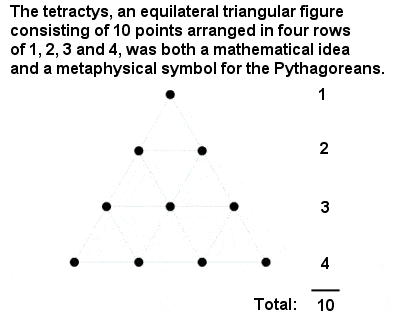 |
The Pythagorean Tetractys |
The holiest number of all was “Tetractys” or ten, a triangular number composed of the sum of one, two, three and four. It is a great tribute to the Pythagoreans’ intellectual achievements that they deduced the special place of the number 10 from an abstract mathematical argument rather than from something as mundane as counting the fingers on two hands.
However, Pythagoras and his school – as well as a handful of other mathematicians of ancient Greece – was largely responsible for introducing a more rigorous mathematics than what had gone before, building from first principles using axioms and logic. Before Pythagoras, for example, geometry had been merely a collection of rules derived by empirical measurement.
Pythagoras discovered that a complete system of mathematics could be constructed, where geometric elements corresponded with numbers, and where integers and their ratios were all that was necessary to establish an entire system of logic and truth.
The Pythagorean Theorem
He is mainly remembered for what has become known as Pythagoras’ Theorem (or the Pythagorean Theorem): that, for any right-angled triangle, the square of the length of the hypotenuse (the longest side, opposite the right angle) is equal to the sum of the square of the other two sides (or “legs”).
Written as an equation: a2 + b2 = c2.
What Pythagoras and his followers did not realize is that this also works for any shape: thus, the area of a pentagon on the hypotenuse is equal to the sum of the pentagons on the other two sides, as it does for a semi-circle or any other regular (or even irregular( shape.
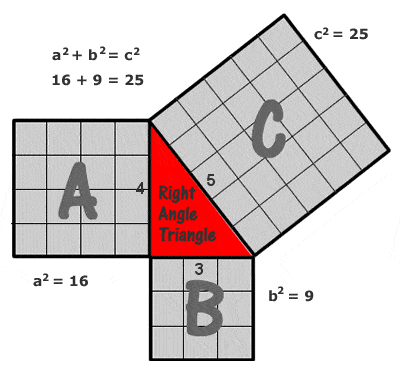 |
Pythagoras’ (Pythagorean) Theorem |
The simplest and most commonly quoted example of a Pythagorean triangle is one with sides of 3, 4 and 5 units (32 + 42 = 52, as can be seen by drawing a grid of unit squares on each side as in the diagram at right), but there are a potentially infinite number of other integer “Pythagorean triples”, starting with (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. It should be noted, however that (6, 8, 10) is not what is known as a “primitive” Pythagorean triple, because it is just a multiple of (3, 4, 5).
Pythagoras’ Theorem and the properties of right-angled triangles seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry, and it was touched on in some of the most ancient mathematical texts from Babylon and Egypt, dating from over a thousand years earlier. One of the simplest proofs comes from ancient China, and probably dates from well before Pythagoras’ birth. It was Pythagoras, though, who gave the theorem its definitive form, although it is not clear whether Pythagoras himself definitively proved it or merely described it. Either way, it has become one of the best-known of all mathematical theorems, and as many as 400 different proofs now exist, some geometrical, some algebraic, some involving advanced differential equations, etc.
It soom became apparent, though, that non-integer solutions were also possible, so that an isosceles triangle with sides 1, 1 and √2, for example, also has a right angle, as the Babylonians had discovered centuries earlier. However, when Pythagoras’s student Hippasus tried to calculate the value of √2, he found that it was not possible to express it as a fraction, thereby indicating the potential existence of a whole new world of numbers, the irrational numbers (numbers that can not be expressed as simple fractions of integers). This discovery rather shattered the elegant mathematical world built up by Pythagoras and his followers, and the existence of a number that could not be expressed as the ratio of two of God’s creations (which is how they thought of the integers) jeopardized the cult’s entire belief system.
Poor Hippasus was apparently drowned by the secretive Pythagoreans for broadcasting this important discovery to the outside world. But the replacement of the idea of the divinity of the integers by the richer concept of the continuum, was an essential development in mathematics. It marked the real birth of Greek geometry, which deals with lines and planes and angles, all of which are continuous and not discrete.
Among his other achievements in geometry, Pythagoras (or at least his followers, the Pythagoreans) also realized that the sum of the angles of a triangle is equal to two right angles (180°), and probably also the generalization which states that the sum of the interior angles of a polygon with n sides is equal to (2n – 4) right angles, and that the sum of its exterior angles equals 4 right angles. They were able to construct figures of a given area, and to use simple geometrical algebra, for example to solve equations such as a(a – x) = x2 by geometrical means.
The Pythagoreans also established the foundations of number theory, with their investigations of triangular, square and also perfect numbers (numbers that are the sum of their divisors). They discovered several new properties of square numbers, such as that the square of a number n is equal to the sum of the first n odd numbers (e.g. 42 = 16 = 1 + 3 + 5 + 7). They also discovered at least the first pair of amicable numbers, 220 and 284 (amicable numbers are pairs of numbers for which the sum of the divisors of one number equals the other number, e.g. the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, of which the sum is 284; and the proper divisors of 284 are 1, 2, 4, 71, and 142, of which the sum is 220).
Music Theory
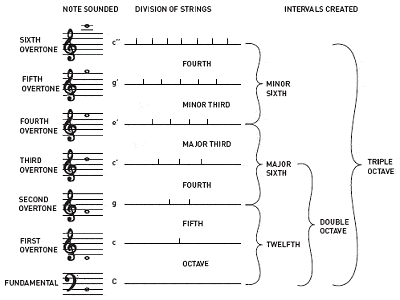 |
Pythagoras is credited with the discovery of the ratios between harmonious musical tones |
Pythagoras is also credited with the discovery that the intervals between harmonious musical notes always have whole number ratios. For instance, playing half a length of a guitar string gives the same note as the open string, but an octave higher; a third of a length gives a different but harmonious note; etc.
Non-whole number ratios, on the other hand, tend to give dissonant sounds. In this way, Pythagoras described the first four overtones which create the common intervals which have become the primary building blocks of musical harmony: the octave (1:1), the perfect fifth (3:2), the perfect fourth (4:3) and the major third (5:4). The oldest way of tuning the 12-note chromatic scale is known as Pythagorean tuning, and it is based on a stack of perfect fifths, each tuned in the ratio 3:2.
The mystical Pythagoras was so excited by this discovery that he became convinced that the whole universe was based on numbers, and that the planets and stars moved according to mathematical equations, which corresponded to musical notes, and thus produced a kind of symphony, the “Musical Universalis” or “Music of the Spheres”.
<< Back to Greek Mathematics | Forward to Plato >> |
