Cofunction Identities – Explanation & Examples
We already know the different trigonometric functions like sine, cosine, and tangent. But how can we determine the relationsip between them? The answer is cofunction identities. In Geometry, two angles are called complementary if their sum is equal to $90^{\circ }$. For example, if $m∠A = 20^{\circ }$, the complement of $m∠A = 70^{\circ }$ because $20^{\circ } + 70^{\circ } = 90^{\circ }$. Now, why this is important? Well, the cosine of $20^{\circ }$ is equal to the sin of $70^{\circ }$.
Clearly, $\displaystyle \cos (20^{\circ })= 0.9$ and $\displaystyle \sin (70^{\circ })= 0.9$. In other words, $\displaystyle \cos (20^{\circ })= \sin (70^{\circ })$ if $20^{\circ }$ and $70^{\circ }$ are complementary. Here, the equation $\displaystyle \cos (20^{\circ })= \sin (70^{\circ })$ is also known as the cofunction identity.
The cofunction identities establish the connection between the trigonometric functions. The soul of this connection is purely based on complementary angles.
It is very important to understand the concept involving trigonometric cofunction identities to prepare yourself for the advanced topics. In this lesson, we will learn:
- What cofunction identities are, and where they come from.
- How we can write and relate one function in terms of its cofunction.
- How to determine the cofunctions of cos, sin, and tan.
- A step by step process of how to solve cofunction identities with a variety of examples
The goal of this lesson is to clear up any confusion you might have about cofunction identities.
What are cofunction identities?
To better understand the meaning of cofunction identities, let me first briefly explain what cofunctions are.
Have you ever realized that the words ‘cofunctions‘ and ‘complementary’ begin with the prefix ‘co-‘? What about the ‘co‘ at the beginning of the words ‘cosine,’ ‘cosecant,’ and ‘cotangent’ when dealing with trigonometric functions? Do you think it is just a trigonometric accident that came from a Mathematical Bing bang?
The ‘co’ at the start of the word ‘cosine’ tells something important about cosine and sine. It is merely two functions that are related — cofunctions. Similarly, secant and cosecant are cofunctions. The same goes with the third pair of trigonometric functions, i.e., tangent and cotangent.
Now, let us try to understand what cofunction identities are and where they come from. Let us begin with an example.
There is a right triangle $ABC$ where $∠A$ and $∠B$ are two reference angles, and $∠C$is the right angle in the diagram below.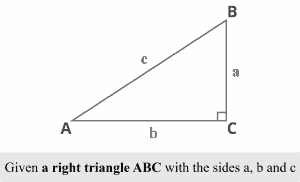
We know that the sum of angles of any triangle is $180^{\circ }$. Also, the right angle measures $90^{\circ }$. Thus, the sum of $∠A$ and $∠B$ is $90^{\circ }$, which means they are complementary angles.
Now, let us determine the ratios of trigonometric functions for both $∠A$ and $∠B$ using the diagrams below.
For reference angle A:
Consider a right triangle $ABC$ with respect to the reference angle $A$ in the diagram below.
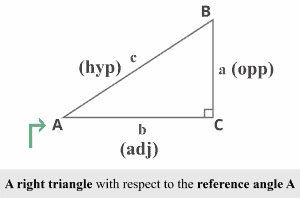
Using $∠A$ as the refernece angle, the $3$ trigonometric ratios as:
- ${\displaystyle \sin A ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$
- ${\displaystyle \cos A ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$
- ${\displaystyle \tan A ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$
It is clear that the side $a$ is the opposite and the side $b$ is adjacent to the reference angle $A$. The side $c$ opposite to the right angle $C$, termed as the the right triangle’s hypotenuse — the longest side.
Now, we can easily determine the trigonometric ratios for reference angle $A$.
- ${\displaystyle \sin A ={\frac {a}{c}}}$
- ${\displaystyle \cos A ={\frac {b}{c}}}$
- ${\displaystyle \tan A ={\frac {a}{b}}}$
For reference angle B:
Consider a right triangle $ABC$ with respect to the reference angle $B$ in the diagram below.
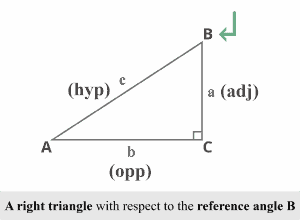
Using the reference angle $B$, the side $b$ is the opposite, and the side $a$ is the adjacent. The Trigonometric ratios for reference angle $B$ would be:
- ${\displaystyle \sin B ={\frac {b}{c}}}$
- ${\displaystyle \cos B ={\frac {a}{c}}}$
- ${\displaystyle \tan B ={\frac {b}{a}}}$
The summary of the results is in the table below:
For reference angle $A$ | For reference angle $B$ |
${\displaystyle \sin A ={\frac {a}{c}}}$ | ${\displaystyle \sin B ={\frac {b}{c}}}$ |
${\displaystyle \cos A ={\frac {b}{c}}}$ | ${\displaystyle \cos B ={\frac {a}{c}}}$ |
${\displaystyle \cos A ={\frac {b}{c}}}$ | ${\displaystyle \tan B ={\frac {b}{a}}}$ |
Let’s carefully analyze the trigonometric ratios for the reference angles $A$ and $B$. As shown above, we can easily figure out some relationship between the two.
While carefully analyzing sin and cosine, we can determine that:
${\displaystyle \sin A ={\frac {a}{c}}}$ and ${\displaystyle \cos B ={\frac {a}{c}}}$
In other words,
${\displaystyle \sin A=\cos B ={\frac {a}{c}}}$
Similarly,
${\displaystyle \cos A ={\frac {b}{c}}}$ and ${\displaystyle \sin B ={\frac {b}{c}}}$
In other words,
${\displaystyle \cos A=\sin B ={\frac {b}{c}}}$
Here, the reference angles A and B are complementary angles where the sine of first reference angle A is equal to the cosine of the other reference angle B.
We need to remember that complementary angles are always acute angles. As we also know that $∠A$ and $∠B$ are complementary angles, so
$m∠A+m∠B=90^{\circ }$
$m∠B=90^{\circ }-m∠A$
Now, plug the value into the original result
${\displaystyle \sin A= \cos (90^{\circ } – m∠A)}$
${\displaystyle \cos A= \sin (90^{\circ } – m∠A)}$
Now, let us replace $m∠A$ with $\theta$ as shown below, we can easily determine the connection between sin and cosine
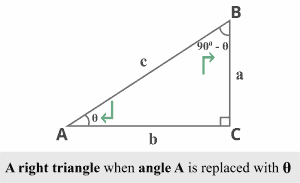
Where sine of angle $\theta$ equals the cosine of its complementary angle $(90^{\circ } – \theta)$ and vice versa. |
Thus, sine and cosine are termed cosine functions. Also, $\sin \theta = \cos (90^{\circ } – \theta)$ and $\cos \theta = \sin (90^{\circ } – \theta)$ are the cofunction identities.
Such calculations generate three pairs of cofunction identities which are:
In Radians | In Degrees |
♦ Sine and cosine cofunctions $\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)$ $\cos \theta =\sin \left({\frac {\pi }{2}}-\theta \right)$ | ♦ Sine and cosine cofunctions $\sin \theta = \cos (90^{\circ } – \theta)$ $\cos \theta = \sin (90^{\circ } – \theta)$ |
♦ Secant and cosecant cofunctions $\sec \theta =\csc \left({\frac {\pi }{2}}-\theta \right)$ $\csc \theta =\sec \left({\frac {\pi }{2}}-\theta \right)$ | ♦ Secant and cosecant cofunctions $\sec \theta = \csc (90^{\circ } – \theta)$ $\csc \theta = \sec (90^{\circ } – \theta)$ |
♦ Tangent and cotangent cofunctions $\tan \theta =\cot \left({\frac {\pi }{2}}-\theta \right)$ $\cot \theta =\tan \left({\frac {\pi }{2}}-\theta \right)$ | ♦ Tangent and cotangent cofunctions $\tan \theta = \cot (90^{\circ } – \theta)$ $\cot \theta = \tan (90^{\circ } – \theta)$ |
How to solve cofunction identities?
We have already discussed the cofunction identities, and where they came from, let us learn how to solve the problems involving cofunction identities.
For example, if we need to find the value of $\theta$ if $\cos(\theta +10^{\circ }) = \sin(\theta +20^{\circ })$, what will we do?
We already know that sine and cosine are cofunctions of each other, so the equation will be true only if the angles are complementary. In other words,
$\theta+10^{\circ }+\theta+20^{\circ }=90^{\circ }$
$2\theta+30^{\circ }=90^{\circ }$
$2\theta=90^{\circ } – 60^{\circ }$
$2\theta=60^{\circ }$
$\theta=30^{\circ }$
Thus, the value of $\theta$ must be $30^{\circ }$ if $\theta$ if $\cos(\theta +10^{\circ }) = \sin(\theta +20^{\circ })$.
In another example,
Given
- $\sin 30^{\circ }=0.5$
- $\cos 30^{\circ }=0.9$
- $\tan 30^{\circ }=0.6$
what is value of $\cos 60^{\circ }$, $\sin 60^{\circ }$ and $\cot 60^{\circ }$?
We know that sin and cosine are cofunctions of each other.
Also,
${\displaystyle \cos (A)=\sin (B)}$ if $A + B = \sin 90^{\circ }$
As
$30^{\circ }+60^{\circ }=90^{\circ }$, so $30^{\circ }$ and $60^{\circ }$ are complementary angles.
So,
$\cos 60^{\circ }=\sin 30^{\circ }$
Since,
$\sin 30^{\circ }=0.5$
Thus,
$\cos 60^{\circ }=0.5$
Similarly,
We know that ${\displaystyle \sin (A)=\cos (B)}$ if $A + B = \sin 90^{\circ }$
As
$30^{\circ }+60^{\circ }=90^{\circ }$, so $30^{\circ }$ and $60^{\circ }$ are complementary angles.
So,
$\sin 60^{\circ }=\cos 30^{\circ }$
Since,
$\cos 30^{\circ }=0.9$
Thus,
$\sin 60^{\circ }=0.9$
Similarly,
We know that tangent and cotangent are cofucntions of each other.
As
${\displaystyle \cot (A)=\tan (B)}$ if $A + B = \sin 90^{\circ }$
Also,
$30^{\circ }+60^{\circ }=90^{\circ }$, so $30^{\circ }$ and $60^{\circ }$ are complementary angles.
So,
$\cot 60^{\circ }=\tan 30^{\circ }$
Since,
$\tan 30^{\circ }=0.6$
Thus,
$\cot 60^{\circ }=0.6$
Now, we will determine the cofunctions of cos, sin, and tangent and also learn how we can relate one function in terms of its cofunction.
cofunction of cos
From the table, we can get
$\cos \theta = \sin (90^{\circ } – \theta)$
We know that cosine of angle \theta equals the sine of its complement angle $(90^{\circ } – \theta)$. Hence, $\sin (90^{\circ } – \theta)$ is the cofunction of $\cos \theta$.
Let us consider the value of $\theta$ is $28^{\circ }$.
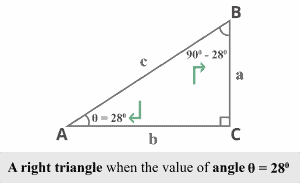
Now, what will be the cofunction identity for $\cos 28^{\circ }$?
The cosine’s cofunction is just the sine.
Using $\cos \theta = \sin (90^{\circ } – \theta)$, and replacing $\theta=28^{\circ }$ we determine
$\cos 28^{\circ } = \sin (90^{\circ } – 28^{\circ })$
$\cos 28^{\circ } = \sin 62^{\circ }$
where $28^{\circ }$ and $62^{\circ }$ are complementary angles as $28^{\circ }+62^{\circ }=90^{\circ }$
Thus, $\sin 62^{\circ }$ is the cofunction of $\cos 28^{\circ }$.
cofunction of sin
From the table, we can get
$\sin \theta = \cos (90^{\circ } – \theta)$
We know that sine of angle $\theta$ equals the cosine of its complement angle $(90^{\circ } – \theta)$. Hence, $\cos (90^{\circ } – \theta)$ is the cofunction of $\sin \theta$.
Again considering $\theta=28^{\circ }$,
Now, what will be the cofunction identity for $\sin 28^{\circ }$?
The sine’s cofunction is just the cosine.
Using $\sin \theta = \cos (90^{\circ } – \theta)$, and replacing $\theta=28^{\circ }$ we determine
$\sin 28^{\circ } = \cos (90^{\circ } – 28^{\circ })$
$\sin 28^{\circ } = \cos 62^{\circ }$
where $28^{\circ }$ and $62^{\circ }$ are complementary angles as $28^{\circ }+62^{\circ }=90^{\circ }$
Thus, $\cos 62^{\circ }$ is the cofunction of $\sin 28^{\circ }$.
cofunction of tan
From the table, we can get
$\tan \theta = \cot (90^{\circ } – \theta)$
We know that tan of angle $\theta$ equals the cotangent of its complement angle $(90^{\circ } – \theta)$. Hence, $\cot (90^{\circ } – \theta)$ is the cofunction of $\tan \theta$.
Again considering $\theta=28^{\circ }$,
Now, what will be the cofunction identity for $\tan 28^{\circ }$?
The tangent’s cofunction is just the cotangent.
Using $\tan \theta = \cot (90^{\circ } – \theta)$, and replacing $\theta=28^{\circ }$ we determine
$\tan 28^{\circ } = \cot (90^{\circ } – 28^{\circ })$
$\tan 28^{\circ } = \cot 62^{\circ }$
where $28^{\circ }$ and $62^{\circ }$ are complementary angles as $28^{\circ }+62^{\circ }=90^{\circ }$
Thus, $\cot 62^{\circ }$ is the cofunction of $\tan 28^{\circ }$.
Example 1
Write $\csc 80^{\circ }$ in terms of its co-function.
Solution:
We know that sec and csc are cofuctions of each other. Using the complementary angles, we know the formula
$\csc \theta = \sec (90^{\circ } – \theta)$
substitute $\theta=80^{\circ }$ in the formula
$\csc 80^{\circ } = \sec (90^{\circ } – 80^{\circ })$
$\csc 28^{\circ } = \sec 10^{\circ }$
Example 2
Write $\cot 50^{\circ }$ in terms of its co-function.
Solution:
We know that tangent and cotangent are cofuctions of each other. Using the complementary angles, we know the formula
$\cot \theta = \tan (90^{\circ } – \theta)$
substitute $\theta=50^{\circ }$ in the formula
$\cot 50^{\circ } = \tan (90^{\circ } – 50^{\circ })$
$\cot 50^{\circ } = \tan 40^{\circ }$
Example 3
Determine the value of $\theta$ for which $\cos \theta = \sin 30^{\circ }$.
Solution:
We already know that sin and cosine are cofunctions of each other. It means the value of $\theta$ must be the complement of $30^{\circ }$.
$\theta+30^{\circ }=90^{\circ }$
$\theta=90^{\circ }-30^{\circ }$
$\theta=60^{\circ }$
Thus, the value of $\theta$ is $60^{\circ }$.
Example 4
Is it true that $\tan (\theta) = \cot (\theta)$? If yes, what is the reason?
Solution:
We know that tan and cotangent are cofunctions of each other. It means we need to deal with complementary angles.
If $\tan (\theta) = \cot (\theta)$, $\theta$ must be the complement of $\theta$.
In other words,
$\theta+\theta=90^{\circ }$
$2\theta=90^{\circ }$
$\theta=45^{\circ }$ (Divide both sides by $2$)
Yes, it is true but the value of $\theta$ must be $45^{\circ }$.
We can also verify that $\tan (\theta) = \cot (\theta)$.
substitute $\theta=45^{\circ }$
$\tan (45^{\circ }) = \cot (45^{\circ })$
$1 = 1$
$L.H.S = R.H.S$
So,
$\cos 60^{\circ }=\sin 30^{\circ }=0.5$ because $30^{\circ }$ and $60^{\circ }$ are complementary angles
