Construction of a 45 Degree Angle – Explanation and Examples

Since a 45-degree angle is half of a 90-degree angle, constructing one requires first creating a right angle and then dividing it in half.

Remember, though, that in pure geometry, we would refer to a 45-degree angle as half of a right angle.

This lesson relies heavily on constructing a perpendicular line and an angle bisector, so make sure to review those before reading on.

In this topic, we will cover:

• How to Construct a 45 Degree Angle
• How to Construct a 45 Degree Angle with Compass
• How to Construct a 45 Degree Angle without a Protractor

How to Construct a 45 Degree Angle

Constructing a 45-degree angle, or half of a right angle, requires first making a right angle and constructing an angle bisector. This will divide the angle into two equal parts, each 45 degrees in measure.

How to Construct a 45 Degree Angle with Compass

First, if we want to construct a 45-degree angle on a line AB, we must construct a right angle on it.

We do this by constructing a perpendicular line to the point A.

We begin by constructing a circle with center A and radius AB. Then, we extend the radius AB to make a diameter and label the circle’s intersection and the line as C. Now, A is the center of the line AC.

Next, we must construct an equilateral triangle on the line CB. Call the third vertex D and connect DA. Recall that DA meets the line CB at a right angle, as we have previously shown.

Next, we need to divide the angle DAB into two equal halves. To do this, we first find the intersection of the circle with center A and radius AB with the line DA. Call this point E and construct the line segment BE.

Now, we can construct an equilateral triangle on BE. We’ll call the third vertex F. Then, we connect FA.

FA bisects the angle DAB. Consequently, the angle FAB is 45 degrees.

How to Construct a 45 Degree Angle without a Protractor

Recall that construction in pure geometry does not involve any measurements. That’s why it is more proper to call what we typically think of as a 45-degree angle “half of a right angle.” This means that it is possible to construct a 45-degree angle using only a compass and straightedge. Because of this, a protractor is not required when we follow the steps outlined above.

Examples

This section will go over common examples involving the construction of a 45-degree angle and their solutions.

Example 1

Given a right angle, construct a 45-degree angle.

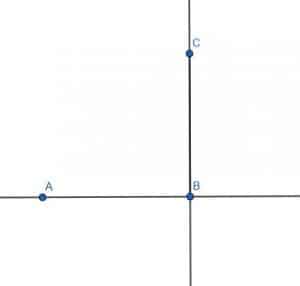
Example 1 Solution

Given that ABC is a right angle, we can construct a 45-degree angle by constructing an angle bisector.

To do this, we construct a circle with center B and radius BC. Call the intersection of BA and this circle D. Then, we can construct the segment CD.

Next, we construct an equilateral triangle with CD as one of the sides. Call the vertex E. Finally, we connect BE. This will be an angle bisector for ABC.

Example 2

Prove that a 45-degree angle is one-fourth of a straight line by constructing four 45 degree angles on a straight line.

Example 2 Solution

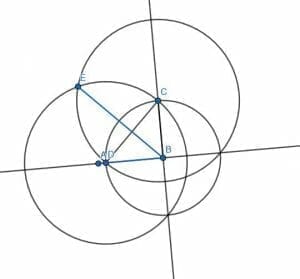
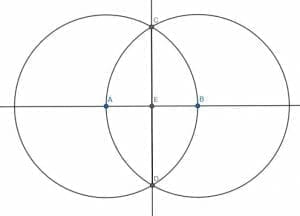
First, we begin with a straight line AB.

Then, we construct a perpendicular line CD. To do this, we construct two circles with radius AB, one centered at A and one centered at B. If we call one of the intersections of this circle C and the other D, the segment CD will be perpendicular to AB. Call the intersection of CD and AB E.

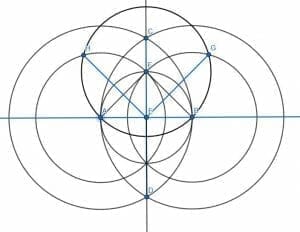
Next, we have to bisect the angles CEB and CEA. First, create a circle with center E and radius EA. Then, label the intersection of this circle and CE as F.

After that, we connect BF and construct an equilateral triangle BFG. Finally, we construct EF, which will be an angle bisector for CEB.

We can also connect the segment AE and construct an equilateral triangle on it. If we connect the third vertex, H, to E, this will bisect the angle CEA.

The angles AEH, HEC, CEG, and GEB, are all 45-degree angles, and together they make the line AB.

Example 3

Construct a 105-degree angle.

Example 3 Solution

105 minus 45 is 60. That is, we can combine a 45-degree angle with a 60-degree angle to get a 105-degree angle.

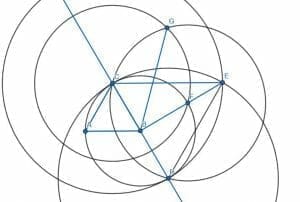
First, construct the equilateral triangle ABC. Each angle of this triangle will be 60 degrees.

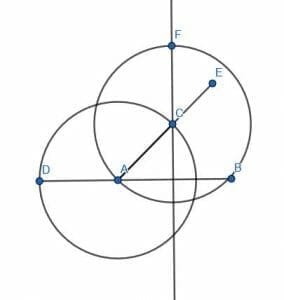
Then, construct a 45-degree angle on the segment BC.

We do this exactly as in example 1. First, create a circle with center B and radius BC. Then, extend BC so that it intersects this circle at the point D. Then, create the equilateral triangle CDE. Next, connect EB. This segment will be perpendicular to CB.

Then, we divide the angle CBE in half as before to get a 45-degree angle CBG. This makes the angle ABG equal to 105 degrees.

Example 4

Construct a regular octagon.

Example 4 Solution

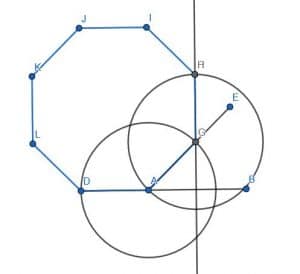
A regular octagon has angles that are 135 degrees. This means that they are equivalent to a right angle with a 45-degree angle. We can also think of this as a straight line minus a 45-degree angle.

This means that we can construct a 45-degree angle on a line AB as we did in example 1. Then, we can extend AB to D as shown.

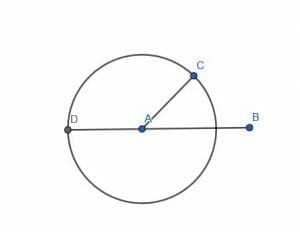
This means that the angle DAC is 135 degrees.

Next, we extend the line segment AC to E. Then, we can construct a 45-degree angle on CE. This makes the angle ACF 135 degrees.

We then continue this pattern for 6 more angles to construct the regular octagon, as required.

Example 5

Construct a 22.5-degree angle.

Example 5 Solution

A 22.5-degree angle is half of a 45-degree angle or one-fourth of a right angle.

We can do this by dividing a 45-degree angle in half.

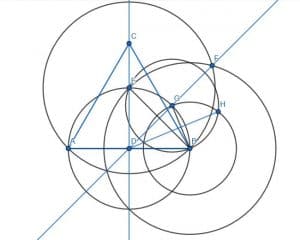
First, we construct a right angle. We can do this by creating an equilateral triangle and creating the angle bisector CD. This makes the right angle CDB.

Next, we divide CDB in half. First, create a circle with center D and radius DB. Label the intersection of CD and this circle as E.

Next, connect BE and construct the equilateral triangle BEF. The segment DF will divide the angle CDB into two equal parts.

Now, we divide the angle FDB into two equal halves. Label the intersection of FD and the circle centered at D with radius DB as G. Then, connect BG and construct the equilateral triangle BGH.

Finally, connect DH. This is the angle bisector for FDB, which means that HDB is a 22.5-degree angle.