Construct a Parallelogram – Explanation and Examples
 Constructing a parallelogram using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines.
Constructing a parallelogram using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines.
A parallelogram will have opposite sides of equal length that are parallel to each other. Rhombi and squares are specific types of parallelograms.
To do this, we must be able to construct parallel lines. Make sure to review this topic and general rules for construction before moving on.
In this section, we will cover:
- How to Construct a Parallelogram
- How to Construct a Parallelogram Given Two Sides
How to Construct a Parallelogram
Recall that we can construct a line parallel to another line. To do this, we use the fact that two lines are parallel if and only if a transversal makes the alternate angles equal. In this case, a transversal is a line that cuts through both of the other lines. Alternate angles, then, are the interior angles on opposite sides.
Since these alternate angles are equal, we can construct a line that crosses a given line. This will be our transversal. Then, we copy the angle formed by the transversal and our original line. We can paste this angle so that it is upside down and on the opposite side of the transversal line. If we extend the leg of the angle that is not the transversal, we have a line parallel to our original line.
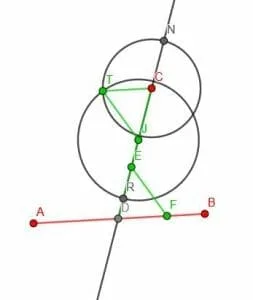
In the figure above, the line segment TC is parallel to the line AB. The transversal is the line EJ, and the alternate angles are EDF and TCJ.
This figure also shows that to copy an angle, we construct a triangle on the angle. Then, since only one triangle can be created using any three side lengths, we copy this triangle. After that, we know that the new triangle’s corresponding angle will be equal to the angle we wanted to copy.
We can use this to construct a parallelogram.
What is a Parallelogram
A parallelogram is a type of quadrilateral or four-sided closed figure created with straight lines. A parallelogram has two sets of parallel sides by definition. A rhombus is a parallelogram where all four sides have the same length. Similarly, a rectangle is a parallelogram where all sides have right angles. A square, then, is a parallelogram with right angles and four equal sides.
Parallelograms have some other interesting features. Their opposite angles are equal in measure, and their opposite sides are equal in length.
How to Construct a Parallelogram Given Two Sides
If we are given two adjacent sides of a parallelogram, say AB and BC, we have to construct a line parallel to AB that intersects C and a line parallel to BC that intersects A.
We can then call the intersection of these two new lines D. The quadrilateral ABCD will be a parallelogram because its opposite sides are parallel.
If we are instead given two parallel lines, we can easily construct a parallelogram. Note, however, that ABCD is a unique parallelogram that uses AB and BC in the situation outlined above. There are infinitely many parallelograms that can be constructed given two parallel lines.
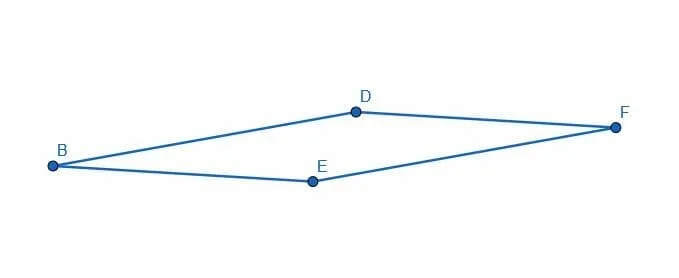
All we have to do is pick a random point on the first parallel line. Let’s call it E. Then, connect A to a random point on the second parallel line, F.
Next, construct any line parallel to EF. We’ll call this line GH. EFGH will also be a parallelogram.
Using Congruent Triangles to Construct a Parallelogram
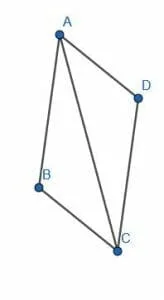
We can also construct a parallelogram using congruent triangles. If we connect two opposite angles of a parallelogram with a line segment, we actually divide the parallelogram into two congruent triangles.
Thus, if we have a triangle, we can copy the triangle so that it is essentially reflected over one of its sides. The new triangle will share a side with the old one and be the mirror image, as shown.
Examples
In this section we will go over common examples of problems involving parallelograms and their step-by-step solutions.
Example 1
Construct a parallelogram on the line segment AB.
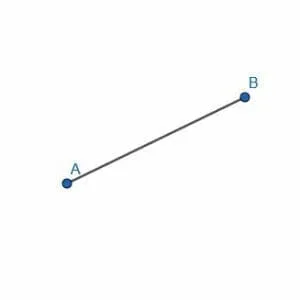
Example 1 Solution
Since we are only given one line segment to work with, we have a lot of freedom in constructing a parallelogram. In fact, there are infinitely many parallelograms that we can construct that have a base AB.
We’ll begin by extending the line AB in both directions.
Next, we need to select another vertex for our parallelogram, C, somewhere in the plane that is not on the line AB.
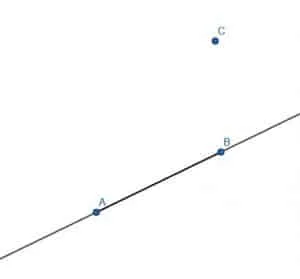
Now, we need to construct a line segment, BC. To keep the construction clear, we will also label a point to the right of A on the line AB as A’ and a point to B’s right on the line AB B’.

Now, since we know that opposite sides of parallelograms are parallel and equal in length, our goal is to construct a segment DC that is parallel to AB and equal in length to construct a parallelogram ABCD. Note, however, that we could have chosen instead to connect the segment AC. In this case, we could have constructed a segment CD’ parallel to AB and equal in length to construct a parallelogram ABD’C. This parallelogram would have had the angle CAB smaller than the corresponding angle DAB in the parallelogram ABCD.
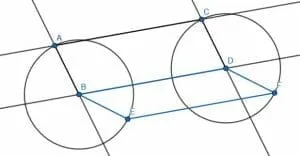
Our first step, then, is to construct a line parallel to AB that goes through C. To do this, we must copy the angle CBB’ so that it becomes BCE.
Copy the Angle
Recall that we do this by constructing a triangle on the angle CBB’. In this case, let’s connect C and B’.
Now, we copy the triangle onto the segment CB so that it CBB’ → BCE.
We can now extend CB to an infinite line. We cut off a segment equal to BB’ with endpoint C pointing away from B to a point F. Then, we cut off a segment equal in length to CB’ with endpoint B pointing away from C to a point J.
Then, we can create two circles. One will have center C and radius CF, while the other will have a center B and radius JB. Label the intersection of these two circles as I, then draw the line CI.
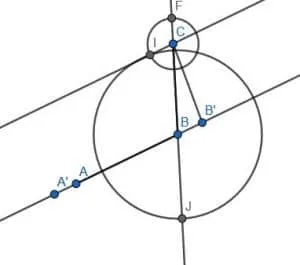
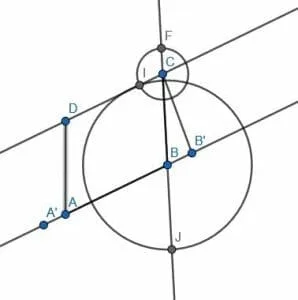
The lines AB and CI are parallel. Now, we need to cut off a segment of CI with length AB and endpoint C. Call this segment DC.
Now, we can connect AD. The figure ABCD will be a parallelogram.
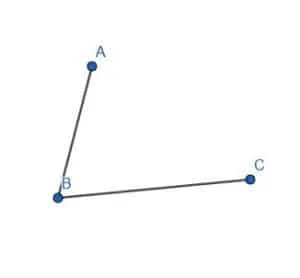
Example 2
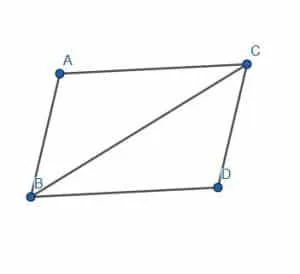
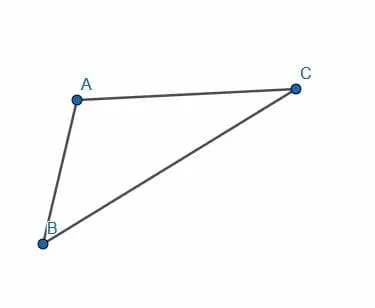
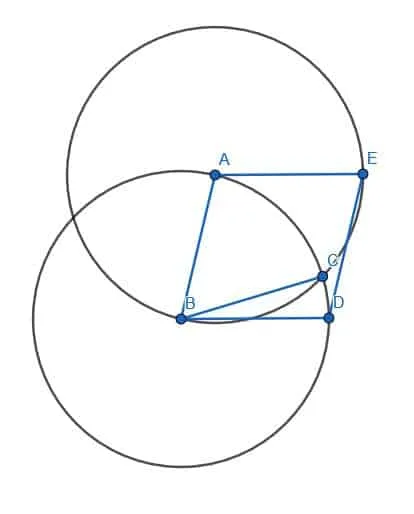
Given the two line segments AB and BC, construct a parallelogram.
Example 2 Solution
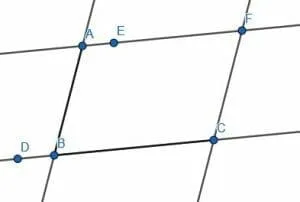
As before, we extend the lines AB and BC. Label the point D on the line BC on the opposite side of C.
Now, copy the angle DBA so that A lines up with B, B lines up with A, and D lines up with a new point E. Then, extend the line AE.
AE is parallel to BC, so we need to cut off a segment equal in length to BC with A as an endpoint. Call this new line segment AD.
Now, we can connect DC. This creates the parallelogram ABCD as required.
Example 3
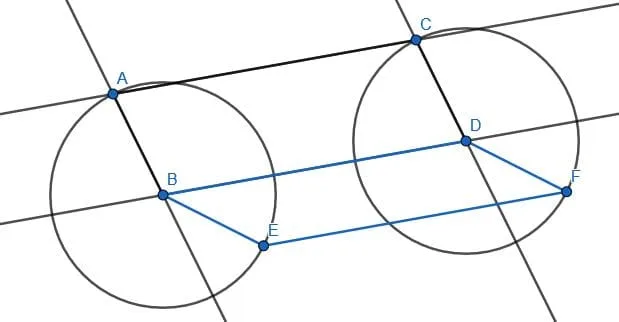
Let AB, CD be two line segments as shown. Construct a parallelogram with segments of length AB and CD.
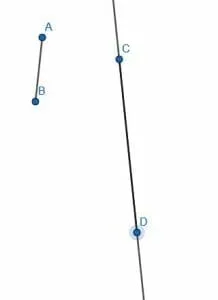
Example 3 Solution
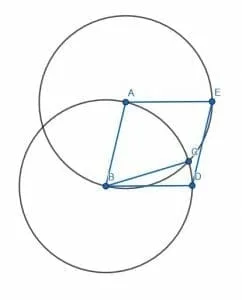
Pick one of the segments to be a leg of the parallelogram we will construct. In this case, we will arbitrarily choose CD. Then, extend the line segment CD.
Now, we need to copy the segment AB onto the endpoint C. Call this new segment CE.
Next, construct a point C’ beyond the point C. We want to copy the angle ECC’ to a new angle CEE’. The new line will be parallel to CD.
Then, we cut off a segment of EF equal in length to CD. When we construct the segment DF, we then create a segment parallel to CE and equal in length. Thus, the constructed figure CDFE is a parallelogram.
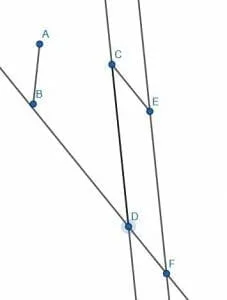
Example 4
Construct a parallelogram on AB with a 60-degree angle.
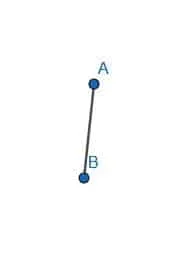
Example 4 Solution
This is a good example to show how we can construct a parallelogram by copying a triangle.
First, create the equilateral triangle ABC on AB.
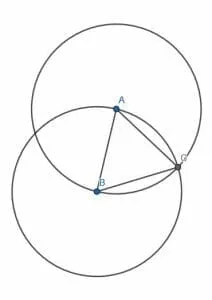
Now, we need to create another equilateral triangle on either AC or BC. We will arbitrarily choose AC and call the third vertex D.
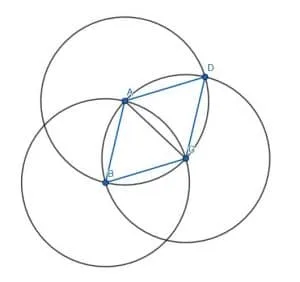
Now, ABCD is a parallelogram because the two triangles ABC and BCD have the same side lengths. The alternate angles DAC and BCA are congruent, which means AD and BC are parallel. Likewise, BAC and ACD are congruent, so AB and CD are parallel.
This parallelogram is actually a rhombus because all of the sides are equal in length.
Example 5
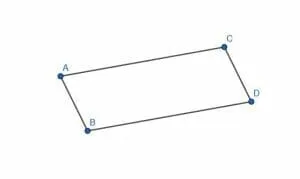
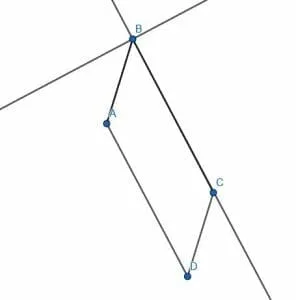
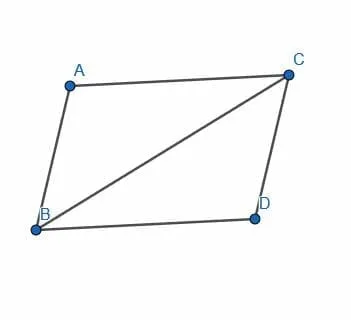
Is the figure shown a parallelogram?
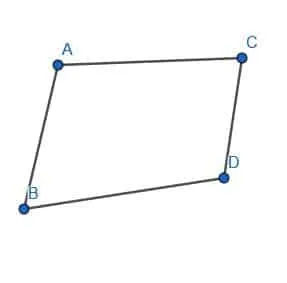
Example 5 Solution
To check whether a figure is a parallelogram, we need to see whether the opposite sides are parallel and whether opposite sides have the same length.
In this case, it looks like AC and BD might not be parallel. However, it’s easier to prove whether one line is longer than another, so we will compare their lengths first.
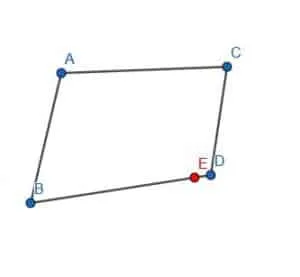
Cut off a segment of BD equal in length to AC. If the endpoint of this segment is not D, the two have different lengths.
We see when we do this that the endpoint, E, is not equal to D. Therefore, AC and BD are of different lengths, so the figure is not a parallelogram.
Practice Problems
- Construct a rhombus with an angle measure other than 60 degrees.
- Construct a parallelogram equal to double the area of the triangle shown.

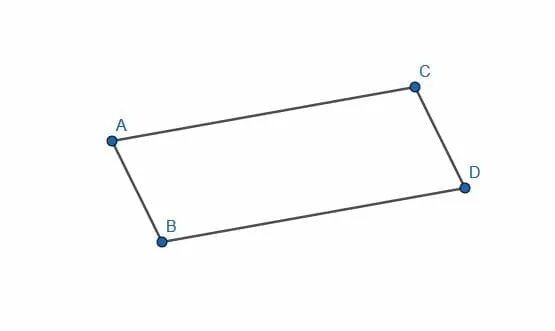
- Create a parallelogram with the same side lengths as ABCD but different angle measures.

- Is the following figure a parallelogram? Why or why not.

- Construct a parallelogram with an angle measure of 45 degrees.
Practice Problems Solutions



- Yes, because the opposite sides have the same length and are parallel to each other.

Images/mathematical drawings are created with GeoGebra.
Practice Questions
![]()
Open Problem Solutions
- Construct a rhombus with an angle measure other than $60$ degrees.
- Construct a parallelogram equal to double the area of the triangle shown.

- Create a parallelogram with the same side lengths as $ABCD$ but different angle measures.

- Is the following figure a parallelogram? Why or why not.

- Construct a parallelogram with an angle measure of $45$ degrees.
Open Problem Solutions



- Yes, because the opposite sides have the same length and are parallel to each other.

Images/mathematical drawings are created with GeoGebra.