Construct a Perpendicular Line – Explanation and Examples

To construct a line perpendicular to a given line, we need to construct an equilateral triangle on the given line and bisect the angle that does not lie on that line.

The angle bisector and the given line will meet at a right angle. Since perpendicular lines meet at right angles, this line is perpendicular to the original line.

Doing this relies on general construction techniques and the ability to construct an equilateral triangle. It is best to review those concepts before moving forward.

In this topic, we will go over:

• How to Construct a Perpendicular Line
• How to Construct a Perpendicular Line to a Point Not on a Line
• How to Construct a Perpendicular Line to a Given Line

How to Construct a Perpendicular Line

Euclid defines a perpendicular line as one which meets another line and makes the adjacent angles equal. Recall that, in pure geometry, there are no measurements, such as degrees. Therefore, although it is tempting to think of a perpendicular line as one that makes two 90 degree angles, we should avoid that temptation and refer to them as two right angles.

There are a few ways to construct a line perpendicular to another. In a general sense, we can construct a line that meets a given line at a right angle. We can also construct this line so that it goes through a given point, not on the given line. Alternatively, we can construct the perpendicular line so that it intersects the line at a given point.

How to Construct a Perpendicular Line to a Point Not on a Line

Suppose that we are given an infinite line through the points A and B and another point, C, which does not lie on the line.

It is possible to construct a line perpendicular to the infinite line AB that passes through the point C.

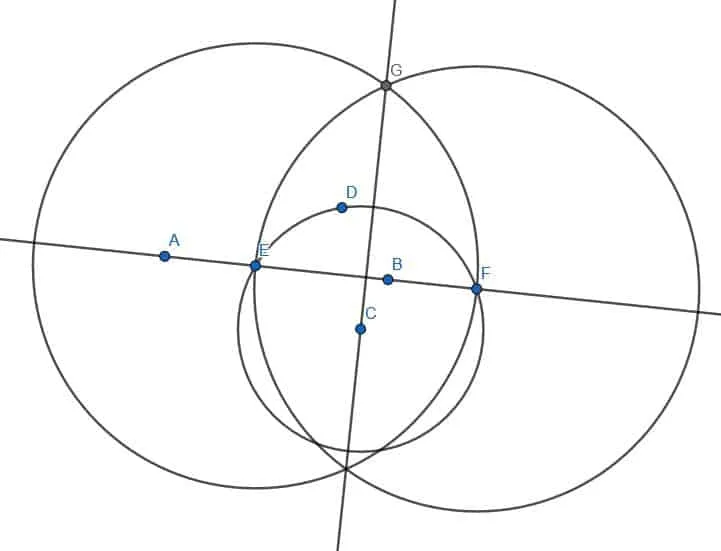
To do this, we first note that the infinite line divides the plane into two sides. We pick a random point D on the opposite side of the plane from C.

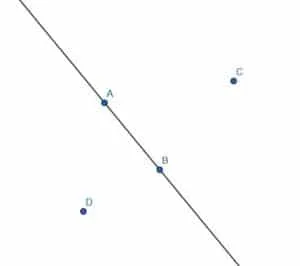
Next, we construct a circle with center C and radius CD. We’ll call the intersections of the line through AB with this circle E and F.

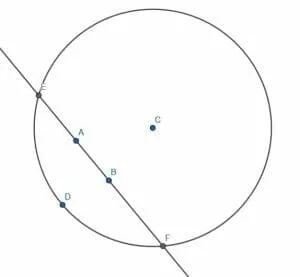
Next, we construct two more circles, each with radius EF. One will have center E, and the other will have center F.

We will label the two intersections of these two circles as H and G. If we construct a line segment, HG, we note that it goes through the point C and meets the line through AB at right angles.

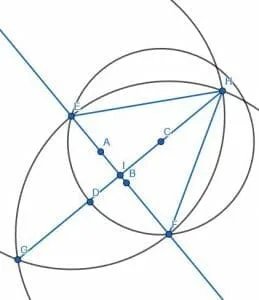
Proof

First, we note that the line segment HI bisects the angle  (proof here) EHF.

Therefore, since EH=FH, HI is equal to itself, and the angles EHI and FHI are equal, the triangles EHI and FHI are congruent. This means that the corresponding angles, namely HIE and HIF, are congruent. Since these angles are also adjacent, they are, by definition, right angles. Consequently, HI is perpendicular, and it is clear that it passes through the point C.

How to Construct a Perpendicular Line to a Given Line

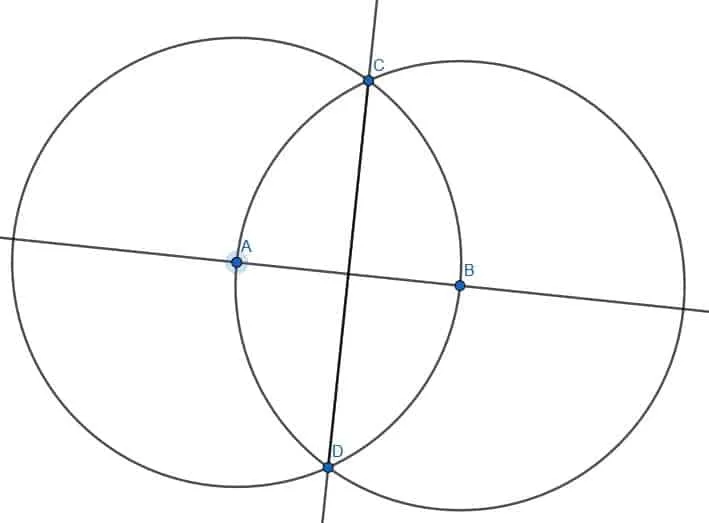
First, suppose we are given an infinite line through points A and B. We want to make a new line perpendicular to this line. That is, we want to construct a line that meets this infinite line at a right angle.

First, we draw two circles with length AB. The first will have center A, while the second will have center B. Label the intersection of these circles as C and draw segments AC and BC. The triangle ABC will be equilateral.

Then, we must bisect the angle ACB. We can skip a few steps in bisecting the angle because AC and BC are already the same length and AB already exists. We can then label the other intersection of the circles with center A and B as D and connect AD and BD. ABD will also be an equilateral triangle. If we construct the segment CD, we will bisect the angle ACB.

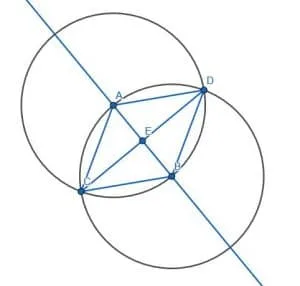
Proof that the Lines are Perpendicular

We can prove that the lines are perpendicular by proving that the angle AEC is equal to BEC’s angle.

AC=BC because they are both legs of an equilateral triangle, ACE=BCE because CE bisects ACB, and CE is equal to itself. Therefore, since the triangles, ACE and BCE, have two sides the same and the angle between those sides the same, the two triangles are congruent. This means that the corresponding angles, namely the adjacent angles AEC and BEC, are congruent. Euclid defines right angles as adjacent angles that are equal and perpendicular lines as those that stand on another line and form two right angles. Therefore, AEC and BEC are right, and CD is perpendicular to the infinite line AB.

We can also prove this algebraically, even though pure geometry should not use angle measures. We know that equilateral triangles have 60-degree angles, and CE bisects the angle ACB. Therefore, in the triangle ACE, the angle ACE has a measure of 30-degrees, and EAC is 60 degrees. Since all triangles have 180 degrees, the remaining angle, CEA, has a measure of 180-(30+60)=90 degrees.

Examples

This section will go over common examples of problems relating to the construction of perpendicular lines and their step-by-step solutions.

Example 1

Construct a line perpendicular to the given line AB.

Example 1 Solution

To do this, we construct the equilateral triangle ABC. Then, bisect the angle ACB and draw the line through the segment AB. Label this intersection D.

AC=BC, CD is equal to itself, and the angles ACD and BCD are equal. Therefore, the triangles ACD and BCD are congruent, and, specifically, the angles CDA and CDB are equal. Since these angles are also adjacent, the angles are right angles, and CD is consequently perpendicular to AB.

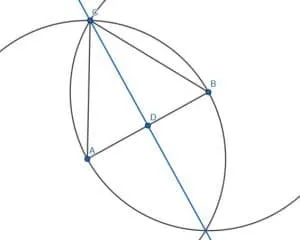
Example 2

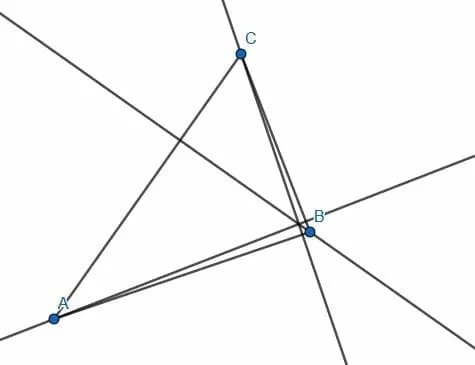
Construct a line perpendicular to each leg of the given triangle.

Example 2 Solution

To do this, we will create six circles. Two will have radius AB with one centered at A and the other centered at B. Another two will have radius CA with one centered at A and another at C. Finally, and the last two will have radius CB with one centered at C and another at B.

We then connect the intersections of circles with the same radius.

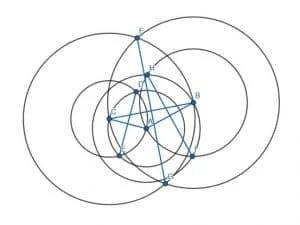
These new segments, HI, DE, and GF, will be perpendicular to the legs AB, CA, and BC, respectively.

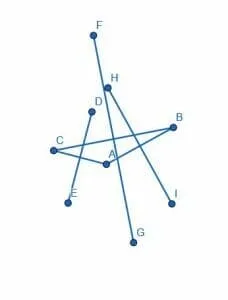
Example 3

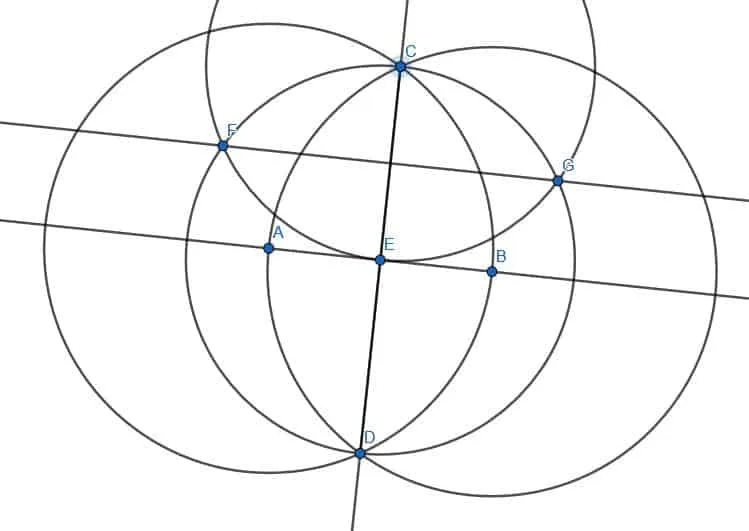
Construct a line perpendicular to a given line. Then, construct a line perpendicular to this new line.

Example 3 Solution

We proceed as before. First, construct a line perpendicular to the first line by creating two circles with radius AB with one centered at A and another at B. Then, connect the intersections of these two circles to form a perpendicular line CD. Call the intersection of AB and CD E.

Now, we want to form a line perpendicular to CD. If we try to construct two circles with radius CD centered at C and D, however, we see that the line AB lies on their intersections. That is, we don’t get a new perpendicular line.

To solve this, we pick a different pair of points on the line CD, say D and E. Then, we construct two circles with D and E at the center, each with radius DE. When we connect these circles’ intersections, we get a new perpendicular line, FG, which is parallel to AB.

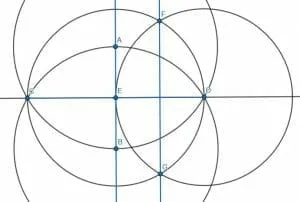
Example 4

Construct a figure to show why the line AB must be infinite to find a line perpendicular to AB and a given point C.

Example 4 Solution

Let’s consider a pair of infinite lines, one vertical and one horizontal. Their intersection is E, and the vertical line has a segment AB. Suppose E does not lie on AB and that the point C lies somewhere else on the horizontal line.

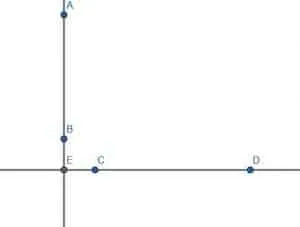
Now, suppose we were given a problem where AB was a given finite straight line and C a point not on it. If we tried to connect C to the line AB at a right angle, we could not do it since the segment would be CE, and E is not on AB.

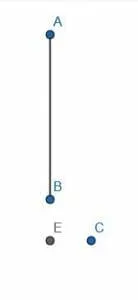
Example 5

Construct a line perpendicular to AB through the point C and another line perpendicular to AB through the point C’. What is the relationship between these two lines?

Example 5 Solution

As before, we find a point D on the other side of the line AB and construct the circle with center C and radius CD. We then label the intersections of this circle and the line AB as E and F. Then, we construct two circles with radius EF, one with center E and one with center F. Call the intersections of these two circles G and H, then connect G, and H. GH is perpendicular to AB.

We also do the same with D’, E’, F’, G’, and H’.

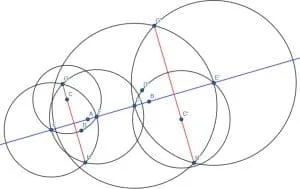
The lines GH and G’H’ will be parallel to each other since they are perpendicular to the same line.