JUMP TO TOPIC
Construct a Square- Explanation and Examples
 Constructing a square using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines with equal length that meet at right angles.
Constructing a square using a compass and straightedge means we construct a space enclosed by two pairs of parallel lines with equal length that meet at right angles.
A square is a special kind of parallelogram. It can also be classified as a special rhombus and a special rectangle.
To construct this, we must be able to construct parallelograms and perpendicular lines. Make sure to review these topics and general rules for construction before moving on.
In this section, we will cover:
- How to Construct a Square
- How to Construct a Square Inscribed in a Circle
How to Construct a Square
A square is a quadrilateral figure with four sides. Each angle is ninety degrees, and opposite sides are, consequently, parallel.
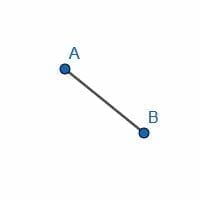
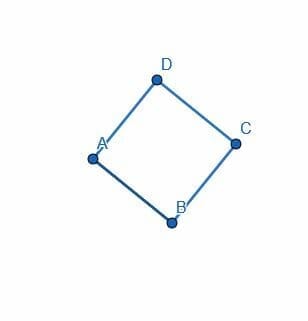
There are a few different ways to construct a square. We’ll discuss one way to do that, given a side with length AB.
First, we construct a line perpendicular to AB that intersects A. Then, we cut off a segment of this new line equal in length to AB, which we will call AC.
We can now construct a line perpendicular to AC that goes through C and another line perpendicular to AB that goes through B. These two lines will intersect at a point we’ll call D.
Then, the figure ABDC will be a square.
Proof the Figure is a Square
The angles are perpendicular by construction. The sides AB and AC are constructed to be the same length. CD is perpendicular to a line perpendicular to AB, which makes it parallel to AB. Likewise, BD is perpendicular to a line perpendicular to AC, which makes it parallel to AC.
Thus, ABDC is a parallelogram because opposite sides are parallel and opposite angles are equal. Therefore, AB=CD and BD=AC. Since AB=AC, all four sides are equal in length.
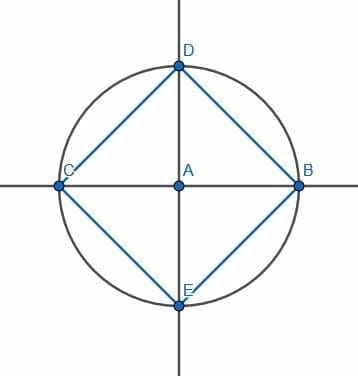
How to Construct a Square Inscribed in a Circle
It is also possible to construct a square inside of a circle such that each vertex of the square falls on the circumference of the circle.
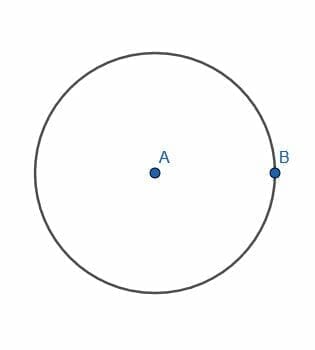
Suppose we have a circle with center A and radius AB. We will extend the radius to a diameter and call the other end C.
Then, we construct a perpendicular bisector for BC. Since A is the center of the circle and BC, this new line, DE, will also be a diameter as it passes through the circle’s center.
If we connect the segments CD, DB, BE, and EC, we will have a square CDBE.
We can prove this is true by looking at the four triangles ACE, AEB, ABD, and ADC. The central angle in each is, by construction, a right angle. The two legs making up these angles in each triangle are all radii of the circle with center A and radius AB. Therefore, all four triangles are congruent, and their third sides, namely CE, EB, BD, and DC, are all equal in length.
These four triangles are all isosceles triangles because two of their legs are radii of the circle with center A and radius AB. Since they are also right triangles, their other two angles are both 45 degrees. This means that the angles of the quadrilateral CEBD, which are each made up of two 45 degree angles, are right angles.
Thus CEBD is a square.
Examples
This section will go over common examples of problems involving the construction of a square and their step-by-step solutions.
Example 1
Construct a square on the line AB.
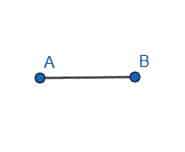
Example 1 Solution
First, we need to construct a line perpendicular to AB. We’ll call this line AC. Then, we need to cut off a segment of AC equal in length to AB. We’ll do this by constructing a circle with center A and radius AB.
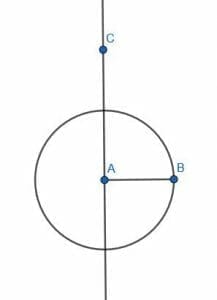
We can then label the intersection of this circle and AC as D. AD will be equal in length to AB because they are radii of the same circle.
We construct a line perpendicular to AC at D and a line perpendicular to AB at B. Call the intersection of these two line segments E. ABDE is a square with side length AB, as required.
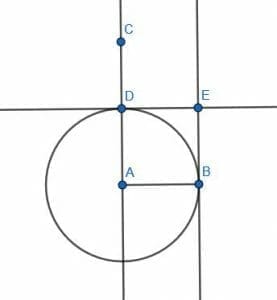
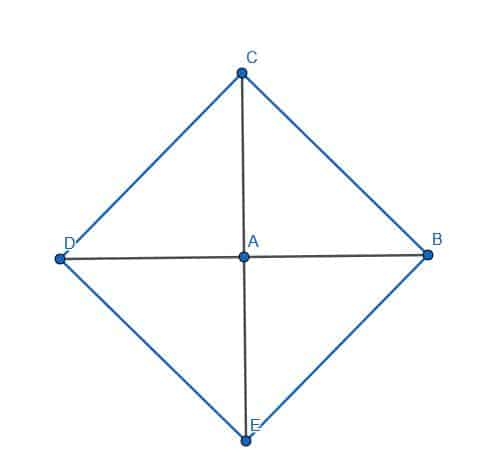
Example 2
Inscribe a square in the circle with center A and radius AB.
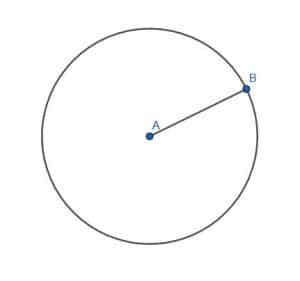
Example 2 Solution
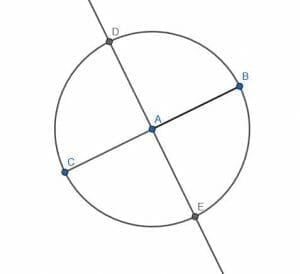
First, we create a diameter for the circle BC through A. Then, we can create a perpendicular bisector for BC.
Since A is the center of BC, the perpendicular bisector will also go through A, making it a diameter of the original circle. Call the intersections of this line and the circumference of the circle D and E.
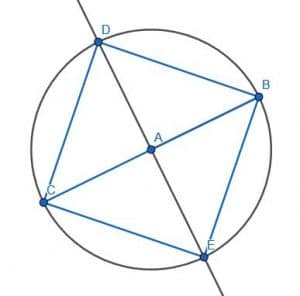
Then, we can connect the four points that lie on the circumference. The figure CDBE will be a square as required.
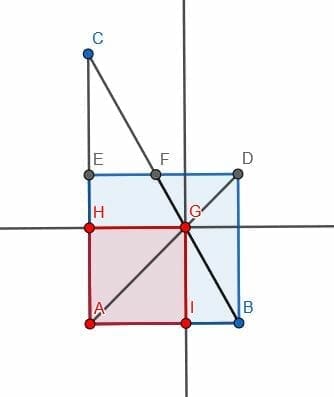
Example 3
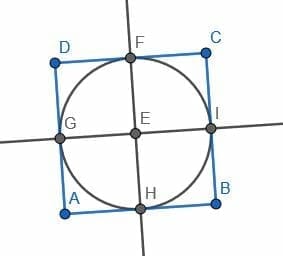
Construct a square so that the center of each side touches the circumference of the circle.
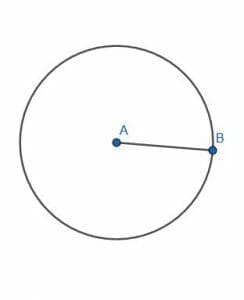
Example 3 Solution
In this case, we will create a diameter BC and a perpendicular bisector DE as in example 2.
This time, we will also create two lines perpendicular to BC at B and C. Then, create two lines perpendicular to DE at D and E.
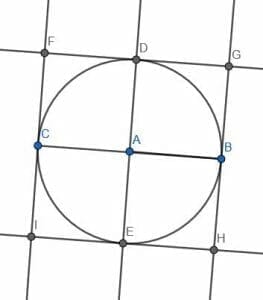
Call the intersections of these lines F, G, H, and I. The figure FGHI creates a square whose sides touch the circumference of the given circle.
Example 4
Construct a square on the diagonal of the given square.
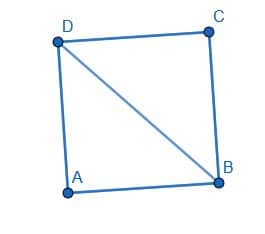
Example 4 Solution
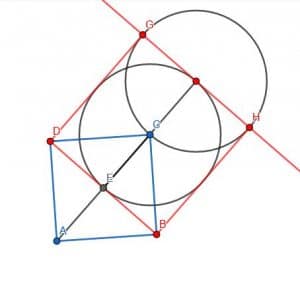
There are a few different ways to do this. We’ll construct the other diagonal AC and label the intersection of the two diagonals as E.
Then, we construct a circle with center C and radius CE. Draw a diameter for this circle, EF, and, after that, construct another circle with center F and radius FC.
Next, construct a line perpendicular to F and label each line’s intersections and the circle with center F and radius FC as G and H.
The quadrilateral GHBD will be the required square.
Example 5
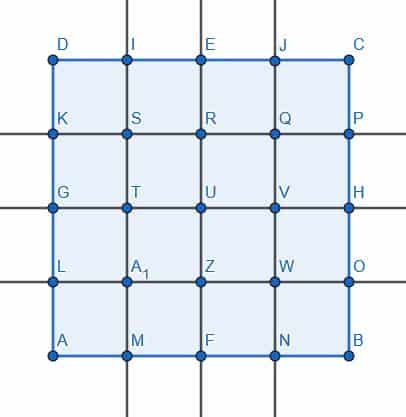
Divide the square into four smaller squares.
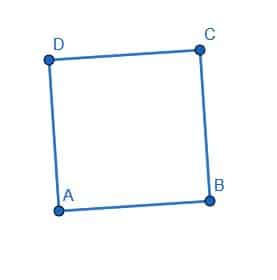
Example 5 Solution
We’ll divide the square by creating a perpendicular bisector for the segments DC and CB. Label their intersection as E. Then, label the center of DC as F, the center of DA as G, the center of AB as H, and the center of CB as I.
If we construct the circle with center E and radius EF, we see that the squares DFCI, EIBH, EHAG, and EGDF all have the same side length.
Practice Questions
![]()
Open Problems
- Construct a circle with side length $AB$.

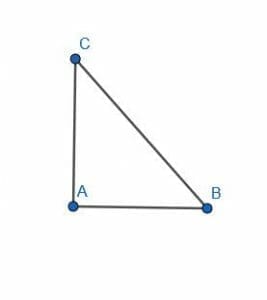
- Construct a square inside the right triangle.

- Inscribe a square in the given circle.

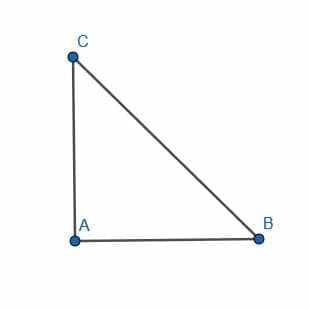
- Construct a circle by creating three more copies of the given right isosceles triangle.

- Divide the given square into sixteen equal squares.
Open Problem Solutions
Images/mathematical drawings are created with GeoGebra.