Dilation in Geometry — Examples and Explanation
 A dilation in geometry is a transformation that changes the size of an object without changing the overall shape of the object.
A dilation in geometry is a transformation that changes the size of an object without changing the overall shape of the object.
The size of the object increases if the dilation factor is greater than 1. If the factor is between 0 and 1, the size decreases, and such dilations are sometimes called compressions.
Before continuing, make sure to review geometric transformations and coordinate geometry.
This section covers:
- What is a Dilation in Geometry?
- How to Do Dilationss in Geometry
- Geometric Dilation Definition
What is a Dilation in Geometry?
In geometry, dilation is a specific type of transformation that changes the object’s size while keeping its general shape the same.
Translations, reflections, and rotations are all rigid transformations because they maintain the object’s size and shape. They change the location and/or orientation of the object.
Dilations are not rigid transformations because the size of the object will change.
Dilation Factor
The dilation factor indicates how much larger (or smaller) the object becomes after the transformation.
For example, if the dilation factor is two, then the object doubles in size. That is, all of its side lengths double in length.
Likewise, if the dilation factor is one-half, then the transformed object is half the original size. Specifically, all of its side lengths will be half of the originals.
Note that this means you cannot dilate a point. Dilations only work for objects with at least two dimensions, such as line segments or polygons.
Dilations and Area
Consider a square for a moment. What happens to the area of the square when the side lengths double?
The area will not double. It will increase by a square factor. For example, a square with side length two has an area of four. A square with side length four has an area of 16. $\frac{16}{4}=4=2^2$
This is true when the dilation factor is another number. If the side lengths triple, the area of the new square is 36. $\frac{36}{4}=9=3^2$.
Dilations vs. Compressions
Sometimes, transformations that change an object’s size but maintain the overall shape are divided into two categories, namely dilations and compressions.
When distinguished, dilations are transformations that increase the size of the object. Compressions, on the other hand, are transformations that decrease the size of the object.
Put differently, if the object increases by a factor greater than 1, the transformation is a dilation. If the object increases by a factor less than 1 but greater than 0, the transformation is a compression.
All factors must be positive, and the transformation that changes the object’s size by a factor of 1 is trivial. Therefore, these are the only two possible cases.
Note, however, that it is common to refer to all transformations that change the object’s size as “dilations,” regardless of whether or not the transformation increases or decreases the size of the given object. That is the language we will use throughout this topic.
The Fixed Point
The fixed point of a dilation indicates where the transformed object will be in the coordinate plane. It is the point that maps to itself in the transformation.
However, the fixed point does not have to be on the figure, which can be a bit confusing. In this case, the distance between the figure’s key points and the fixed point also increases by the factor of dilation.
How to Do Dilations in Geometry
When dilating a figure in geometry, begin by finding the key points of the object. These will be endpoints, vertices, and centers.
Then, find the fixed point. If the point is not a key point of the object, draw a line from the key points to the fixed point.
Next, multiply the length of each line segment in the object (including the ones drawn in the previous step) by the factor of dilation.
Draw the new figure in the coordinate so that the fixed point is in the same spot.
Functions
It is also possible to dilate functions. Unlike other geometric objects, a function dilation applies to either its vertical or horizontal components.
A vertical dilation by a factor greater than 1 stretches the function up and down. A dilation by a factor between 0 and 1 not-inclusive compresses the function.
In this case, transformations applied to the x-values of a function operate in a kind of “mirror world” and are the opposite of what we expect. A horizontal dilation by a factor greater than 1 squishes the function horizontally, while a dilation by a factor between 0 and 1 not-inclusive stretches it.
The fixed point for a horizontal dilation is x=0, the y-intercepts, and the fixed point for a vertical dilation is y=0, the x-intercept(s).
Mapping Notation
The mapping notation for a dilation with a fixed point (0, 0) by a factor of $a$, where $0<a<∞$ and $a≠1$ on a geometric object is:
$(x, y) → (ax, ay)$.
If the fixed point is not the origin, then this should be followed by a translation to get the fixed point back to its original location in the plane.
When the object is a function with a vertical dilation by a factor $a$ as defined above, the function mapping notation is:
$f(x)→af(x)$.
When the object is a function with a horizontal dilation by a factor $a$ as defined above, the function mapping notation is:
$f(x)→f(\frac{1}{a}x)$.
Geometric Dilation Definition
A geometric dilation is a transformation that changes the size of a geometric object by a given factor from a given point without changing its overall shape. This factor is greater than 0 and not equal to 1.
Examples
This section covers common examples of problems involving geometric dilations and their step-by-step solutions.
Example 1
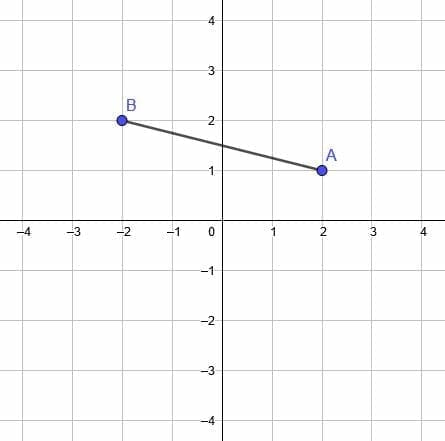
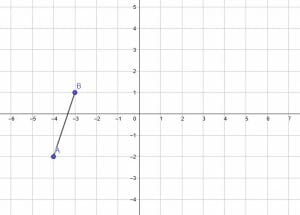
Dilate the given line segment by a factor of 2 with the fixed point A. Then, dilate the original segment by a factor of 2 with the origin as the fixed point. Compare.
Example 1 Solution
Since A is at a point (-4, -2) and B is at a point (-3, 1), the length of the segment AB is $\sqrt(10)$. Therefore, the length of the new segment, A’B’ will be $2\sqrt(2)$.
The first transformation requires A to be the fixed point. This means that A and A’ are the same. Then, we need to draw a line segment of length $2\sqrt(2)$ with endpoint A.
There are, of course, infinitely many ways to do that. A’B’ should be oriented the same way as AB, though. Therefore, A’B’ will extend past AB such that B is the midpoint of A’B’, as shown.
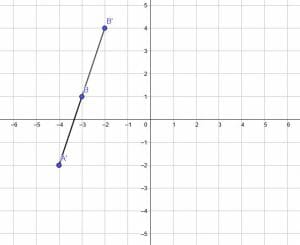
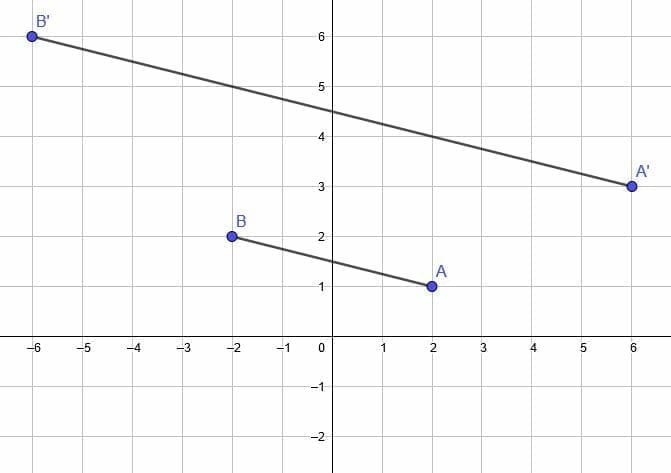
When the fixed point is instead the origin, it helps draw a line from the origin to each of the endpoints A and B.
Then, extend each of these lines. In this case, we will double their lengths because the dilation factor is 2.
A” and B” are then located at the ends of these new segments.
The distance from the origin to B is $\sqrt(10)$, so the distance from the origin to B” is $2\sqrt(10)$ in the same direction.
The distance from the origin to A is $2\sqrt(5)$. Therefore, the distance from the origin to A” is $4\sqrt(5)$ in the same direction.
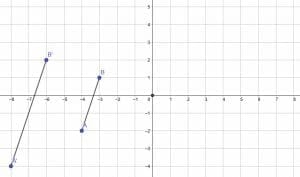
Both A’B’ and A”B” have the same length and the same slope. The only real difference is their location on the coordinate plane.
Example 2
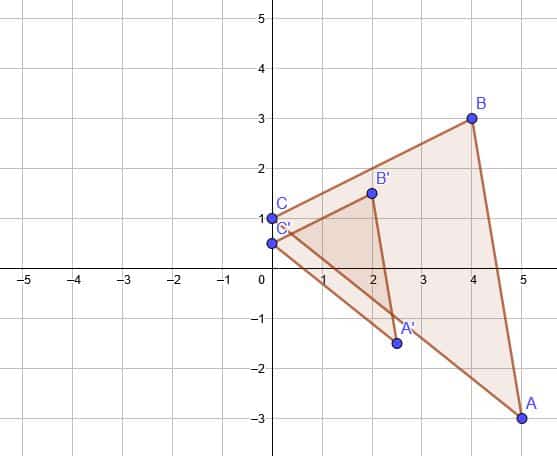
Dilate the triangle ABC by a factor of $\frac{3}{5}$ with the fixed point A.
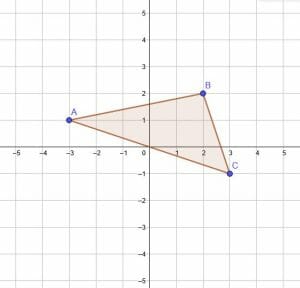
Example 2 Solution
As in this example, a dilation does not have to be by a factor of a whole number.
In this case, we can first dilate the figure by a factor of $\frac{3}{5}$ with a fixed origin. This way, we can easily figure out the new figure’s size without having to do as many calculations.
Remember that when the origin is fixed, we can map the vertices in the following way:
$(x, y) → (ax, ay)$.
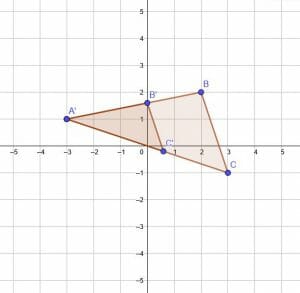
In the figure given, the vertices are A(-3, 1), B(2, 2), and C(3, -1). Therefore, after a dilation about the origin, the new vertices are A'($\frac{3}{5}×-3, \frac{3}{5}×1$), B'($\frac{3}{5}×2, \frac{3}{5}×2$), and C'($\frac{3}{5}×3, \frac{3}{5}×-1$), which simplify to A'($-\frac{9}{5}, \frac{3}{5}$), B'($\frac{6}{5}, \frac{6}{5}$), and C'($\frac{9}{5}, -\frac{3}{5}$).
Then, find a translation from A’ back to A. The difference in x-values for the two points is $-\frac{9}{5}+3=\frac{6}{5}$. Similarly, the difference in y-values for the two points is $\frac{3}{5}-1=-\frac{2}{5}$.
Therefore, to get from A’ back to A, the figure A’B’C’ must shift $\frac{6}{5}$ units to the left and $\frac{2}{5}$ units upward. This makes the new coordinates of B’ and C’ ($0, \frac{8}{5}$) and ($\frac{3}{5}, -\frac{1}{5}$).
Example 3
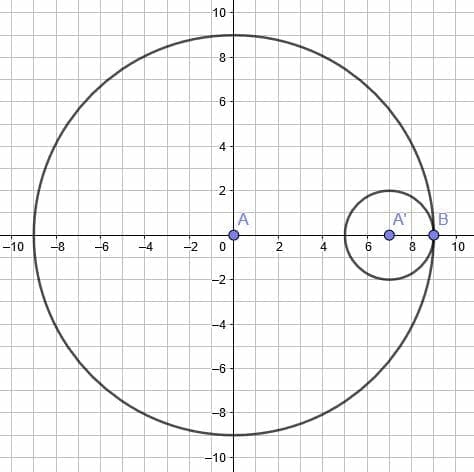
Dilate the circle by a factor of $\frac{4}{3}$ using its center as the fixed point.
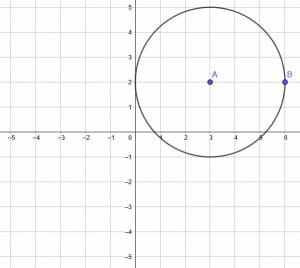
Example 3 Solution
This figure does not have any line segments, so we need to construct one. It makes the most sense to construct the line segment, AB, which will also be a radius of the circle.
It is possible to dilate the circle with respect to the origin and then translate the new object so that the center lines up with A. For circles, however, it is relatively easy to apply a dilation to the center because we only need to know the length of one line, the radius, and choose a horizontal or vertical line to make calculations simple.
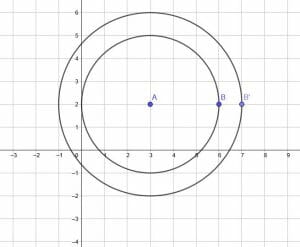
The length of AB is 3. Since the dilation factor is $\frac{4}{3}$, the length of the radius of the new circle is $\frac{4}{3}×3=4$.
Now, construct a line from A of length 4 units through B. Since B and A lie on the same horizontal, we only have to adjust the y-value of B. $3+4=7$, so the new point, B’ has coordinates (7, 2).
This is enough information to construct the new circle with radius AB’ using a compass.
Example 4
Dilate a quadrilateral shown by a factor of $\frac{1}{3}$ with a fixed point the origin.
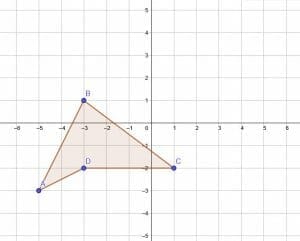
Example 4 Solution
First, find the coordinates of the key points. In this case, the vertices are at A(-5, -3), B(-3, 1), C(1, -2), and D(-3, -2).
Since the fixed point is the origin, the new vertices will be A(-5a, -3a), B(-3a, 1a), C(1a, -2a), and D(-3a, -2a), where a=$\frac{1}{3}$, the factor of dilation.
Therefore, the new vertices are A'($-\frac{5}{3}, -1$), B'($-1, \frac{1}{3}$), C'($\frac{1}{3}, -\frac{2}{3}), and D'($-1, \frac{2}{3}$).
To complete the transformation, connect the points as in the original figure.
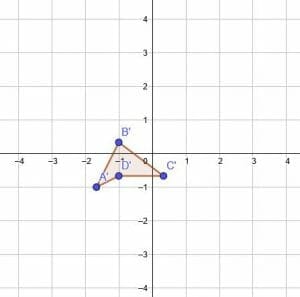
Example 5
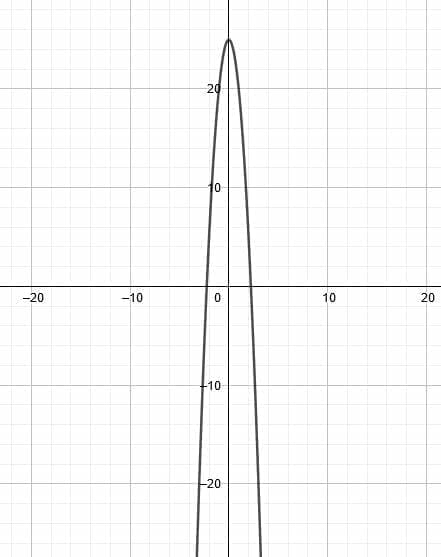
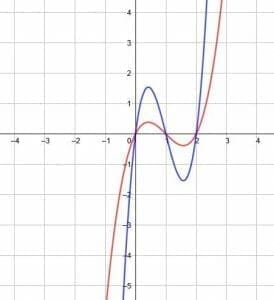
Dilate the function shown by a vertical factor of 4 and horizontal factor of 3.
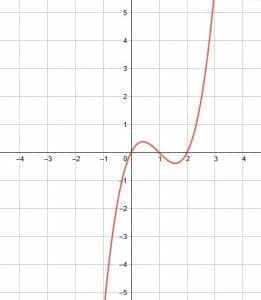
Example 5 Solution
Let’s begin with the horizontal dilation by a factor of 3. Remember, those horizontal transformations are always the opposite expectations. Therefore, a horizontal dilation by a factor of three actually compresses a function by a factor of 3.
This means that all of the x-values of key points will be one-third of their original value. In this function, the key points to note are the x-intercepts, the y-intercept, and the local maximum and minimum.
When the dilation occurs, the height of the maximum and minimum stay the same, as do the x-intercepts.
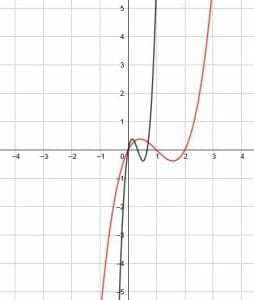
The vertical dilation operates more expectedly. A dilation by a factor of 4 stretches the function upwards by a factor of 4.
This means that the local maximum height will increase by a factor of 4, and the depth of the local minimum will also increase by a factor of 4. The y-intercept, b, will likewise become 4b. In this, however, the y-intercept is 0, so there is no net change.
The x-intercepts, however, will all remain the same.
Practice Questions
![]()
Open Problems
- Dilate the line segment by a factor of $3$ with fixed point $A$.

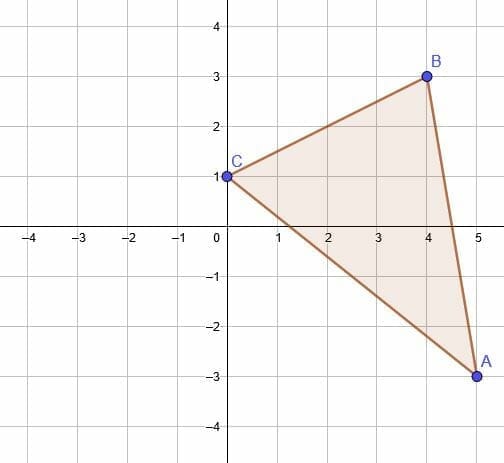
2. Dilate the triangle by a factor of $\frac{1}{2}$ with the origin as the fixed point.
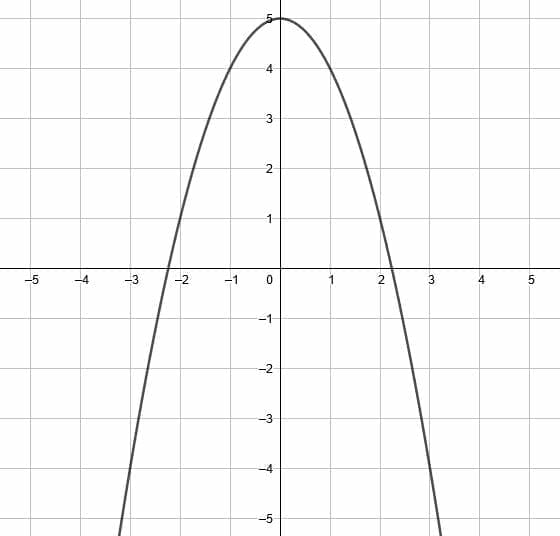
3. Transform the function with a vertical dilation by a factor of
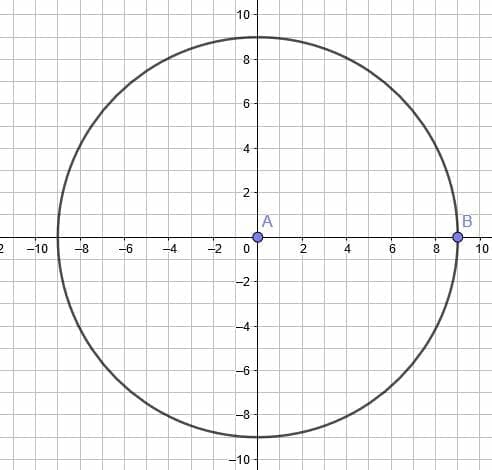
4. Dilate the circle by a factor of $\dfrac{2}{9}$ at point B.
Open Problem Solutions
Images/mathematical drawings are created with GeoGebra.