Even and Odd Identities – Explanation and Examples

Even and odd identities for trigonometric functions involve using the trig function’s evenness or oddness to find the trig values of negative angles.

Specifically, sine, tangent, cosecant, and cotangent are odd functions. The cosine and secant functions are even. Like all trig identities, the even and odd identities play an important role in physical sciences and engineering.

Before moving forward with this section, review even and odd functions and trig identities.

Odd Identities

Odd identities are trigonometric identities that stem from the fact that a given trigonometric function is an odd function. Recall that an odd function is a function $f(x)$ such that $f(-x) = -f(x)$. That is, corresponding positive and negative inputs have outputs with the same absolute value. The signs of these outputs, however, will be different.

Reflecting an odd function over the $x$ axis and then over the $y$ axis (or vice versa) maps the function to itself. That is, odd functions are symmetric about the origin.

In trigonometry, the functions sine, cosecant, tangent, and cotangent are odd. This fact gives the four odd identities:

• $sin(-x) = -sin(x)$
• $csc(-x) = -csc(x)$
• $tan(-x) = -tan(x)$
• $cot(-x) = -cot(x)$

The inverse trig functions arcsine and arctangent are also odd. Therefore, there are also two inverse trig odd identities:

• $arcsin(-x) = -arcsin(x)$
• $arctan(-x) = -arctan(x)$

Even Identities

Even identities in trigonometry are identities that stem from the fact that a given trig function is even. Recall that an even function is a function $f$ such that $f(-x) = f(x)$. That is, corresponding positive and negative inputs have the same output.

Such functions are symmetric about the y-axis, and reflecting them over the y-axis maps them to themselves. There are two even trig functions, cosine and secant. Therefore, there are two trigonometric even identities:

• $cos(-x) = cos(x)$
• $sec(-x) = sec(-x)$

There are no even inverse trig functions.

How Do You Tell If a Sine Function is Odd or Even?

To tell if a sine function is odd or even, you can employ one of two possible ways: algebraically or graphically. Doing this graphically is easier. If the y-axis is a line of symmetry for the function, then it is even. If the function is symmetric about the origin (rotating it 180 degrees or reflecting it over both axes), then it is odd.

Algebraically, one has to prove that, for any $x$, $f(-x) = f(x)$ for a function to be even and that $f(-x) = -f(x)$ for a function to be odd.

Algebraic Proofs of Even and Odd

With trigonometric functions, this is done by looking at the basic definitions of sine and cosine in the context of the unit circle.

Recall that a negative angle on the unit circle measures clockwise, while a positive angle measures counterclockwise.

In the unit circle, the sine of an angle is equal to the height of the right triangle formed with the terminal radius and the x-axis. In the figure shown, the sine of the angle $BAD$ is $DI$. The negative angle corresponding to $BAD$ measures clockwise, so it is $BAE$. In the figure, the sine of this angle is $IE$.

Since $DI$ extends upwards from the x-axis, its length is positive. Since $IE$ extends downwards, its length is negative. However, their magnitudes will be the same.

Similarly, the sine of $BAF$ is $FH$, and the sine of $BAG$, the corresponding negative angle, is $HG$. These two lines also have the same magnitude but different sines.

Therefore, the sines of two angles with an equal magnitude but measured in the opposite direction will have the same magnitude but different signs. Therefore, sine is odd.

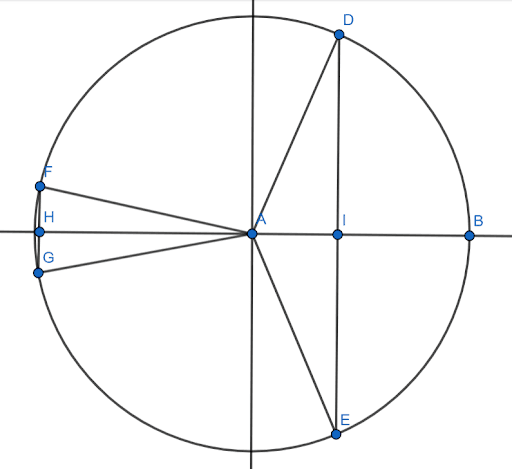
Notice, however, that the cosines (the horizontal line of the right triangle of the angle) are on the same side of the x-axis. For $BAD$ and $BAE$, it is $AI$. For $BAF$ and $BAG, it is $AH$. Therefore, the cosine does not change based on the sign of the angle. Thus, cosine is even.

The odd or evenness of the other trig functions follow from the odd or evenness of sine and cosine.

Even and Odd Transformations

Note that transformations of the function can affect whether they are even or odd.

In particular, horizontal and vertical shifts can make an odd function even or an even function odd. For example $cos(x-\frac{\pi}{2})$ maps cosine to sine. Therefore, $cos(x-\frac{\pi}{2})$ is odd.

Transformations can also make it so that a function is neither odd nor even. The transformation $sin(x)-1$ is an example.

Examples

This section goes over common examples of problems involving even and odd trig identities and their step-by-step solutions.

Example 1

Use the evenness and oddness of sine and cosine to prove that the tangent function is odd.

Solution

It is required to show that tangent is odd. That is, that:

$tan(-x) = -tanx$.

Recall that $tanx = \frac{sinx}{cosx}$. Therefore:

$tan(-x) = \frac{sin(-x)}{cos(-x)}$.

Since sine is odd and cosine is even, this simplifies to:

$tan(-x) = \frac{-sinx}{cosx} = -\frac{sinx}{cosx} = -tanx$.

Example 2

Is the function $y=sinx-1$ even, odd, or neither?

Solution

A simple way to test whether a function is even, odd, or neither is to find the value of the function for a negative angle and positive angle with the same magnitude. In this case, use the angles $\frac{\pi}{2}$ and $-\frac{\pi}{2}$.

At $\frac{\pi}{2}$, sine is equal to $1$. Therefore, $sinx-1 = 0$.

At $-\frac{\pi}{2}$, sine is equal to $-1$. Therefore, $sinx-1 = -2$.

Therefore, this function is neither odd nor even.

Take note, however, that this method can give a clue about whether a function is odd or even but not prove it. For example, $sin(\pi) = 0 = sin(-\pi)$. At these two points, the function $sinx-1$ is $1$, but the function is not even.

Example 3

Find the sine of $\frac{\pi}{4}$ and $-\frac{\pi}{4}$.

Solution

Recall that the sine of $\frac{\pi}{4}$ is $\frac{\sqrt{2}}{2}$. Additionally, since sine is odd $sin(-x) = -sinx$. Therefore, $sin(-\frac{\pi}{4}) = -sin(\frac{\pi}{4})$.

Thus, $sin(-\frac{\pi}{4}) = -\frac{\sqrt{2}}{2}$.

Example 4

Find the secant of $-\frac{\pi}{6}$.

Solution

Recall that the secant function is the reciprocal of the cosine function. That is, $secx=\frac{1}{cosx}$. Like cosine, it is even.

Therefore:

$sec(-\frac{\pi}{6}) = sec(\frac{\pi}{6})$.

Since the secant of the angle $\frac{\pi}{6}$ radians is $\frac{1}{\frac{\sqrt{3}}{2}} = \frac{2\sqrt{3}}{3}$, the secant of the angle $-\frac{\pi}{6}$ is also $\frac{2\sqrt{3}}{3}$.

Example 5

Use the fact that cosine is even to prove that $cos(x-y) = cos(y-x)$.

Solution

To begin, take note that $y-x = -(x-y)$.

Therefore, $cos(y-x) = cos(-(x-y))$. Since cosine is even, however, $cos(-(x-y)) = cos(x-y)$. Therefore, $cos(y-x) = cos(x-y)$ for any angles $x$ and $y$.