JUMP TO TOPIC
Factors of 10: Prime Factorization, Methods, Tree, And Examples
The Factors of 10 are the numbers that give zero as the remainder whenever 10 is divided from these numbers. The factors of 10 also include the numbers which produce 10 as the product when they are multiplied together.
Figure 1 – All possible Factors of 10
10 $\div$ 2 = 5
Since a whole number quotient is produced, both the divisor 2 and its whole number quotient 5 act as the factors of 10. In this article, we will be taking a closer look at the various methods which are used to determine the factors of 10 and the techniques associated with them.What Are the Factors of 10?
The factors of 10 are 1, 2, 5, and 10. These are the numbers that yield zero as the remainder when 10 is divided from them. These 4 factors also form factor pairs with one another, meaning they produce 10 as the product when multiplied together.The number 10 has a total of 4 factors.How To Calculate the Factors of 10?
You can calculate the factors of 10 through two basic methods – the division method and the prime factorization method. But before calculating the factors of 10 through these methods, let’s first determine the range in which these factors lie.To determine the range in which the factors of 10 lie, firstly, determine the half of that number, i.e, 10. The factors for any even number lie between the smallest factor and half of that number. Since the smallest factor for any number is 1, and the half of 10 is 5, hence the range of factors of 10 will lie between 1 and 5. This indicates that in order to look for the factors of 10, you should look for the numbers lying between 1 and 10.Now let’s take a look at the division method. The condition for a factor through the division method is that it should produce a whole number quotient. Following is the division for all the factors of 10:\[\frac{10}{1} = 10 \]\[\frac{10}{2} = 5\]\[\frac{10}{5} = 2\]\[\frac{10}{10} = 1\]Hence, the factors of 10 are 1, 2, 5, and 10.Factors of 10 by Prime Factorization
Prime Factorization is the technique through which the prime factors for a number are determined. The prime factorization is an extension of the division method technique, the only difference is that prime numbers are used to carry out the division.The prime factorization method carries on until 1 is obtained at the end. The said number goes through the division with a prime number and the whole number quotient produced then goes through the same procedure.This division with prime number continues till 1 is achieved at the end. The prime factorization of the number 10 is shown below:10 $\div$ 2 = 5
5 $\div$ 5 = 1
Since 1 is obtained at the end, hence the prime factors for 10 are given below:Prime Factors of 10: 2, 5
Prime Factorization of 10 can be mathematically written as:Prime Factorization of 10 = 2 x 5
The prime factorization of the number 10 is shown below in figure 1: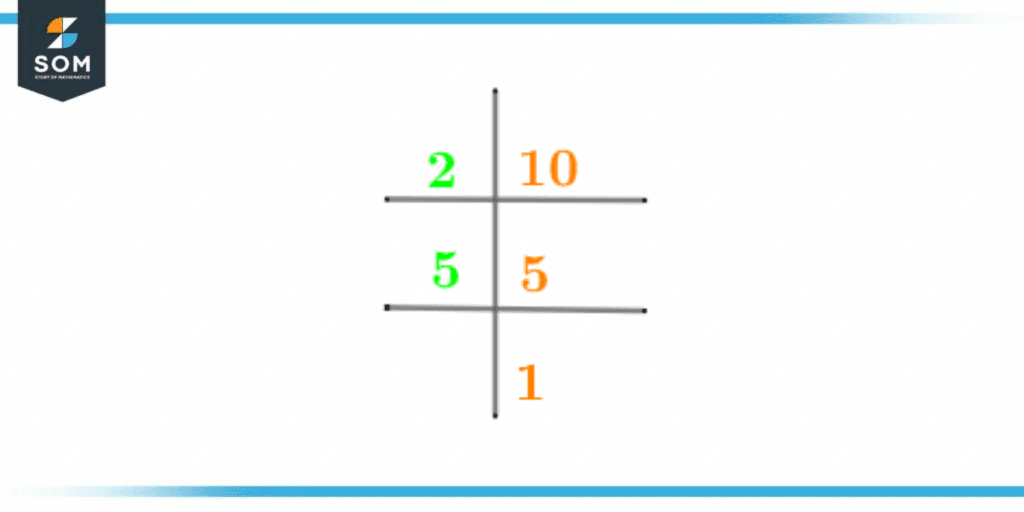
Figure 2 – Prime Factorization of 10
Factor Tree of 10
The Factor Tree is a visual representation of the prime factorization of the number. As the name suggests, the factor tree has the shape of a tree in which branches extend out to potential prime factors. The only difference between factor tree and prime factorization is that the prime factorization technique ends at the number 1 whereas the factor tree ends at the prime factors. The factor tree begins with the number 10 itself and then extends out its branches into a prime factor and the respective whole number quotient. The factor tree of 10 is shown below in figure 2: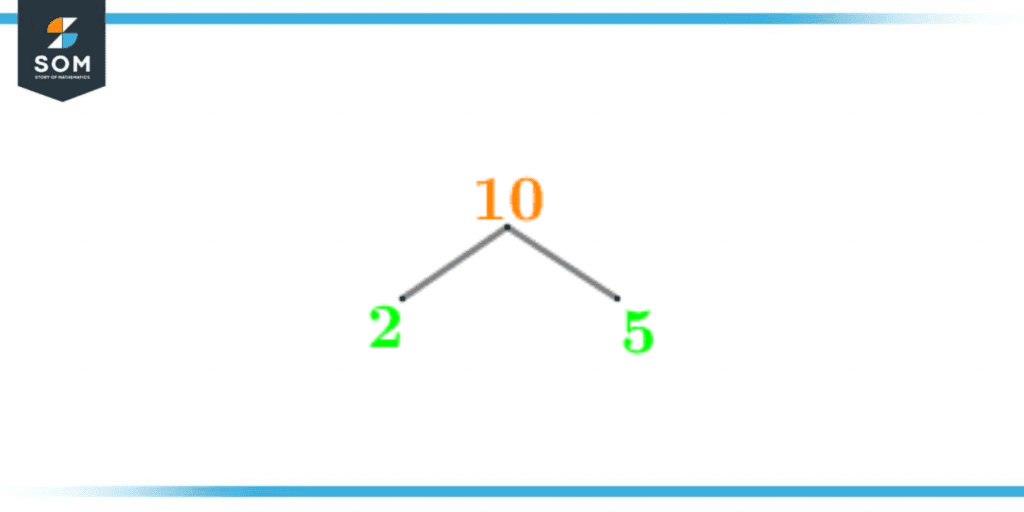
Figure 3 – Factor Tree of 10
Factors of 10 in Pairs
The factors of a number also form factor pairs with one another. A fair pair consists of two numbers which when multiplied together, yield the original number as the product. The factor pairs of the number 10 are given below:1 x 10 = 10
2 x 5 = 10
Hence, the total number of factor pairs for the number 10 is 2 which are given below:Positive factor pairs of 10: (1, 10) and (2, 5)
The factor pairs for any number can be both positive as well as negative. Both the factor pairs are the same but the only difference between the two is the sign. So in this way, the number 10 has 2 positive factor pairs and 2 negative factor pairs.The condition of negative factor pairs is that both the number existing in the pair must have the same sign. This is because when these two numbers will multiply together, they will yield a positive product.The negative factor pairs of 10 are given below:-1 x -10 = 10
-2 x -5 = 10
Negative factor pairs: (-1, -10) and (-2, -5)
Some interesting facts about the number 10 are given below:- The sum of the first three prime numbers (2, 3, 5) gives 10 as the result.
- The majority of the counting systems around the world make use of the base 10 numeral system.
- The very popular metric system is based on the number 10.
- The Neon in the periodic table has an atomic number of 10.
- The sum of the digits of 10 is 1: 1 + 0 =1
- The product of the digits of 10 is 0: 1 x 0 = 0
Factors of 10 Solved Examples
To further enhance the concept of the factors of 10, some solved examples are given below:Example 1
Determine the sum of the first 5 multiples of 10 and divide this number with the sum of the factors of 10.Solution
This example is a two part question. Firstly, let’s deal with the first part. The first 5 multiples of 10 are given below:First 5 Multiples of 10 = 10, 20, 30, 40, 50
Now, calculating the sum of these first 5 multiples of 10:Sum of multiples = 10 + 20 + 30 + 40 + 50
Sum of multiples = 150
Now that we have obtained the sum of the first 5 multiples of 10, our first part of the question comes to an end. Now let’s deal with the second part.The factors of 10 are given below: 1, 2, 5, 10
Calculating their sum:Sum of factors = 1 + 2 + 5 + 10
Sum of factors = 18
Now, divide the sum of the multiples of 10 by the sum of the factors of 10:Result = $\frac{150}{18} $
Result = 8.333
Example 2
Find out the product of the common factors existing between the number 20 and the number 10.Solution
To find the product of the common factors existing between 10 and 20, let’s first list down the factors of 10:Factors of 10 = 1, 2, 5, 10
Now, let’s list down the factors of 20:Factors of 20 = 1, 2, 4, 5, 10, 20
The common factors between 10 and 20 are given below:Common factors = 1, 2, 5, 10
Now, calculating the product of these common factors:Product = 1 x 2 x 5 x 10
Product = 100
So, the product of the common factors existing between 10 and 20 is 100.Example 3
Determine the joint average of the factors of 10 and the factors of 15.Solution
To determine the joint average of the factors of 10 and 15, let’s first list down these factors.Factors of 10 are given below:Factors of 10 = 1, 2, 5, 10
Similarly, the factors of 15 are given below:Factors of 15 = 1, 3, 5, 15
For calculating their joint average, let’s first determine the sum of all these factors.Sum of all factors = Sum of factors of 10 + Sum of factors of 15
Now, let’s determine these parameters.Sum of factors of 10 = 1 + 2 + 5 + 10
Sum of factors of 10 = 18
Similarly, let’s calculate the sum of the factors of 15:Sum of factors of 15 = 1 + 3 + 5 + 15
Sum of factors of 15 = 24
Calculating their joint sum = 18 + 24
Sum of factors = 42
Now since there are 4 factors of 10 and 4 factors of 15, so in total, there are 8 factors.Calculating the average:\[ Average = \frac{42}{8} \]Average = 5.25
So the average of the factors of 10 and 15 is 5.25. Images/mathematical drawings are created with GeoGebra.