JUMP TO TOPIC
Factors of 100: Prime Factorization, Methods, Tree, and Examples
The number 100 is even composite. Natural numbers having more than two factors are known as composite numbers. Factors can also be an algebraic expression that divides other expressions evenly.
Figure 1 – All possible Factors of 100
- Positive Factors.
- Negative Factors
What Are the Factors of 100?
The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100.All these numbers fulfill the condition of factors, which says that when 100 should be uniformly divided by a number, the remainder should be zero. As the number is a composite number, it has more than two factors.How To Calculate the Factors of 100?
You can calculate the factors of 100 by two different methods: Multiplication Method and Division Method.Two numbers are multiplied together, and the product is 100. The multiplicand and the multiplier will be the factors of 100. This technique is known as the multiplication method.When 100 is divided by a number evenly, and the remainder is zero. That number is said to be a factor of 100. This technique is known as the division method.We will discuss both methods in this article and will compare their results.Finding factors of 100 by using the division method:In the division method, we simply divide 100 by different numbers, and if the remainder is zero, that number is considered a factor of 100. Keep in mind that the divisor should not be greater than 100.Always start the division from the smallest integer. The number 1 is the smallest integer in a positive number line.\[ \dfrac {100}{1} = 100 \]\[ \dfrac {100}{-1} = -100 \]1 and -1 is a factor of every whole number because it divides every number uniformly, and the remainder is always zero.100 is an even number. Every even number is divisible by 2.\[ \dfrac {100}{2} = 50 \]\[ \dfrac {100}{-2} = -50 \]The remainder of the above division is zero. Add 2 and -2 to the list of factors.Divide 100 by 3:\[ \dfrac {100}{3} = 33.3 \]The quotient is in decimal form, which means the remainder is not zero. So 3 and -3 are not a factor of 100.We will now divide 100 by a series of numbers that are less ten 100. The calculations are as below:\[ \dfrac {100}{4} = 20 \]\[ \dfrac {100}{-4} = -20 \]\[ \dfrac {100}{5} = 16 \]\[ \dfrac {100}{-5} = -16 \]\[ \dfrac {100}{10} = 10 \]\[ \dfrac {100}{-10} = -10 \]\[ \dfrac {100}{20} = 8 \]\[ \dfrac {100}{-20} = -8 \]\[ \dfrac {100}{25} = 5 \]\[ \dfrac {100}{-25} = -5 \]\[ \dfrac {100}{50} = 4 \]\[ \dfrac {100}{-50} = -4 \]These numbers satisfy the condition of factors. The remainder is zero. By looking at the above division, write the positive and negative factor list of 100.Every number divides itself evenly. As a result, every number is a factor in itself. \[ \dfrac {100}{100} = 2 \]\[ \dfrac {100}{-100} = -2 \]Positive factors list of 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.Negative factors list of 100: -1, -2, -4, -5, -10, 20, -25, -50, and -100.Finding factors of 100 by multiplication method:The numbers whose product is 100, both numbers will be the factors of 100. Multiplier and multiplicand both should be in the range of 1-100. Always start the multiplication from the smallest integer with the greatest integer of the concerning number line (1-100).1 x 100 = 100
Now pick the second factor from the start of the factor list and multiply it by the second-last factor of the list.2 x 50 = 100
Pick the third factor from the start of the list and multiply it by the third last factor in the list:4 x 25 = 100
Multiply the fourth factor in the list by the fourth last factor:5 x 20 = 100
The last factor left is 10. It is multiplied by itself to form 100:10 x 10 = 100
By the above multiplications, we conclude the factors list of 100Positive factors list of 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.We obtained the same factor list by both methods.Fun Facts About 100
- The base for percentage is 100.
- The sum of the first nine prime numbers is 100. The sum is given as 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 = 100.
- There are 100 years in a century.
- The number 100 is a perfect square.
- The square root of 100 is 10.
- The first ten odd numbers add to make 100.
Factors of 100 by Prime Factorization
A number greater than one can be expressed uniquely by the product of its prime factors. This technique is known as Prime factorization. Prime factors are numbers that have two factors only. The number one and the number itself.The upside-down division is simply a division technique used to find the prime factorization of a number. Prime factorization reduces every composite factor into a prime factor and a composite factor. We keep on dividing until the quotient becomes 1.Factors list of 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.Prime Factors of 100: 2 and 5.The number 1 is not a prime factor.Always start the division by the smallest prime factor. Divide 100 by 2\[ \dfrac {100}{2} = 50\]50 is divisible by 2. \[ \dfrac {50}{2} = 25 \]50 is not divisible by 2. So divide it by the next prime factor. Which is the number 5.\[ \dfrac {25}{5} = 5 \]The number 5 is divisible by 5.\[ \dfrac {5}{5} = 1 \]The quotient is 1. Division terminates.The figure below shows the upside-down division of 100: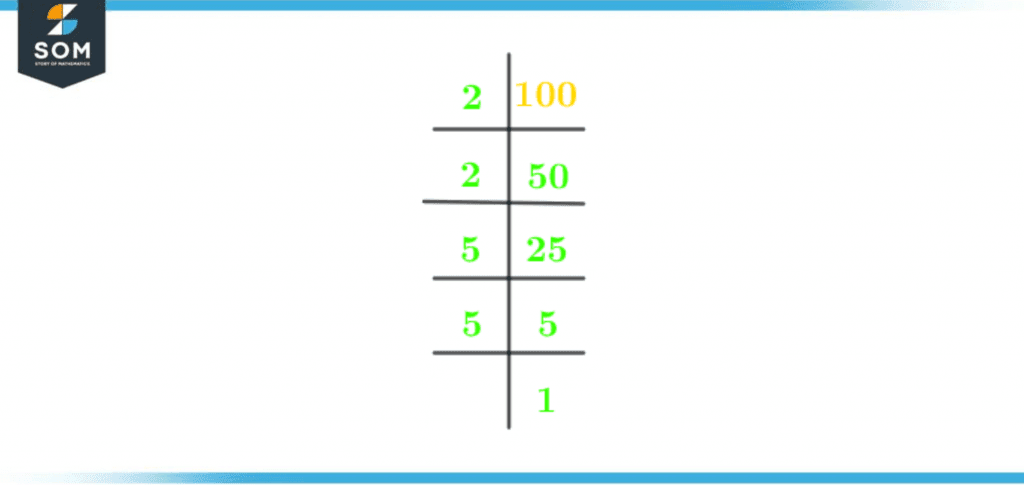
Figure 2 – Prime Factorization of 100
2 x 2 x 5 x 5 = 100
Factor Tree of 100
A factor tree is a graphical representation of factors of 100, mainly prime factors. To construct a factor tree, write the number 100 at the top. Split 100 into its prime and composite factors.\[ \dfrac {100}{2} = 50\]The number 2 is a prime number and can not be further simplified. Divide 50 by 2.\[ \dfrac {50}{2} = 25\]Again the number 2 is prime. The number 25 will be divided by 5.\[ \dfrac {25}{5} = 5\]5 is a prime number. So it will be divided by itself.\[ \dfrac {5}{5} = 1 \]The quotient is 1, and the division terminates.The following is the factor tree of 100: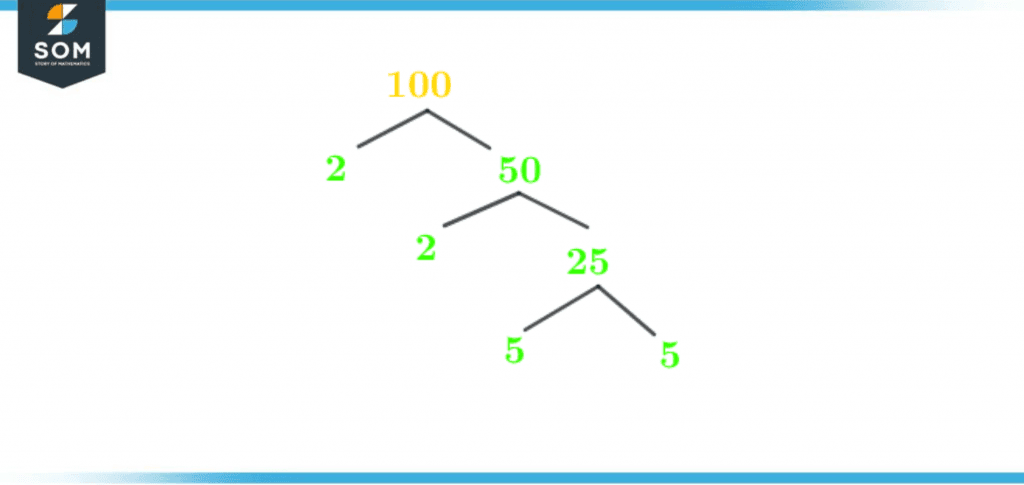
Figure 3 – Factor Tree of 100
Factors of 100 in Pairs
Writing the numbers in sets when multiplied gives 100 are called factor pairs of 100. Factor pairs can not be greater than the number. Factor pairs can be discovered by simply the multiplication method. Factors list of 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.Take the first and last number from the factors list of 100.First factor: 1Last factor: 1001 x 100 = 100
Multiply the corresponding entries of the factors list to get the factor pairs.The second factor paired with the second last factor:2 x 50 = 100
The third factor paired with the third last factor:4 x 25 = 100
The fourth factor paired with the fourth last factor:5 x 20 = 100
The middle factor 10 will be paired with itself:10 x 10 = 100
Positive Factor Pairs of 100: (1, 100) (2, 50) (4, 25) (5, 20) (10, 10)Negative Factor Pairs of 100: (-1, -100) (-2, -50) (-4, -25) (-5, -20) (-10, -10)Factors of 100 Solved Examples
Here are some examples of factors of 100 for a better understanding.Example 1
Help Sammy find the sum factors 100. Divide it by the sum of factors of 10. Also, Find the common factors of 10 and 100.Solution
List of factors of 10: 1, 2, 5, and 10.List of factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, and 100.Finding the sum of factors of 100:S1
1 + 2 + 4 + 5 + 10 + 20 + 25 + 50 + 100 = 217
Finding the sum of factors of 10:S2
1 + 2 + 5 + 10 = 18
Now divide S1 by S2:\[ \dfrac {217}{18} = 12.05\]Finding the common factors of 10 and 100:Common Factors = 1, 2, 5, 10
After comparing both factor lists, we take out the numbers that are part of both lists.List of common factors of 10 and 100: 1, 2, 5, and 10.