JUMP TO TOPIC
Factors of 105: Prime Factorization, Methods, Tree, and Examples
Factors of 105 divide it ultimately, producing a zero remainder. 105 is an odd composite, meaning it has more than two factors. This lesson will look at several methods of calculating these factors in detail.

Figure 1 – All possible Factors of 105
What Are the Factors of 105?
The factors of 105 are 1, 3, 5, 7, 15, 21, 35, and 105. 105 has a total of 8 factors, which shows it is a composite number having several factors.
These 8 factors can be split into 4-factor pairs, and these factors, along with the factor pairs, can be both positive and negative.
How To Calculate the Factors of 105?
The factor of 105 can be calculated through multiple methods like division and prime factorization. But we will look at the division method first as it is simpler to understand and comprehend.
Division
The division method is based on finding a number that gives zero remainders when divided by 105; this number will be a factor of 105. If it is a whole number, the quotient will also be a factor for 105. The use of the division method has been shown below:
\[ \frac{105}{ 2} = 52.5 \ (\text{Not a factor}) \]
\[ \frac{105}{ 3} = 35 \ (factor) \]
\[ \frac{105}{ 5} = 21 \]
As 21 is a whole number, therefore 5 is a factor of 105 along with 21. We will skip six and move on to 7.
\[\frac{105 }{ 7} = 15 \]
\[ \frac{105 }{ 105} = 1 \]
These also divide the number completely; therefore, 1 and 105 are factors of 105.
Through the division method, the factors of 105 are:
Factors of 105 = 1, 3, 5, 7, 15, 21, 35, and 105.
Factors of 105 by Prime Factorization
Prime factorization is, at its roots, a division method, but it uses prime numbers to find out the prime factors of any number. We divide the number with any prime number that divides it entirely and proceeds until one is obtained.
This method is solely based on prime numbers. Prime numbers are all the numbers that are only divisible by themselves or the universal divisor 1. As this method gives us only prime numbers, we call the factors produced prime factors.
Although there exists a familiarity between the division method and prime factorization, the only difference that separates these two is that in prime factorization, we divide using a prime number; the quotient then acts as the dividend for the next step.
The final result we are looking for is a 1.
We are given the number 105. The first thing to look at is whether it is a prime or a composite number; we realize that 105 is not a prime number as it has multiple factors other than 1 and 105. To understand the prime factorization of 105, it is shown below:
105 $\div$ 3 = 35
35 $\div$ 7 = 5 (The quotient 35 acts as the dividend for this step)
5 $\div$ 5 = 1 (The final result equal to 1 is achieved)
This prime factorization was done in several steps, but there is an alternate method of writing it down:
Prime Factorization of 105 = 3 x 7 x 5
The prime factorization of 105 is given shown below:
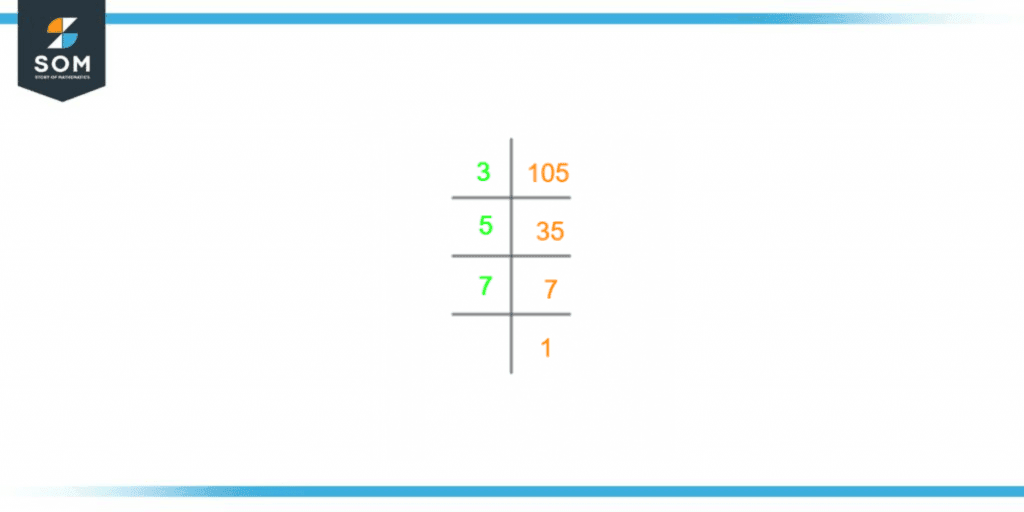
Figure 2 – Prime Factorization of 105
Factor Tree of 105
A factor tree is essentially a representation of the prime factors of any given number in the shape of a tree. At the same time, there are multiple methods of finding factors of any given number. This tool deploys a visual element to the understanding of factors of any number.
The diagram is drawn in the shape of a tree; the original number is written at the head of the tree, which then divides into two branches upon division; at least one of the branches ought to have a prime number. The other is mostly a composite number if the original number was a composite number.
If the original number is a prime, then the tree will only have two branches, but in the case of a composite number, the branches extend further down until all prime numbers are obtained at the tree’s roots. Once these are achieved, no further division is possible, as prime numbers do not divide further.
Although the basic definition of a factor tree and how it is drawn is quite clear, in order to understand it better, we will look at figure 2, which shows precisely how a factor tree is constructed. We can observe that 105 is at the top, and it fleshes out into 3 and 35, which then continues onwards:
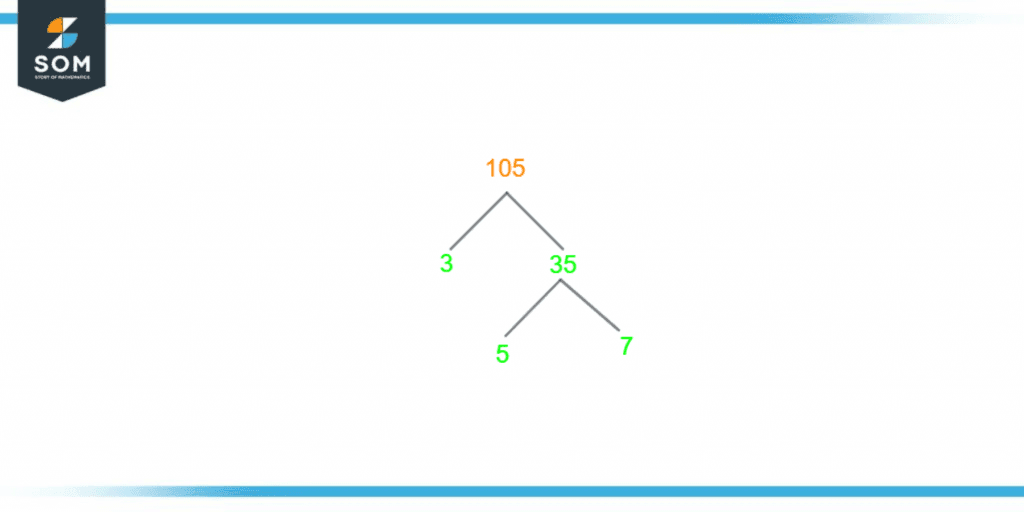
Figure 3 – Factor Tree of 105
Factors of 105 in Pairs
The factor pairs of any number are any two factors that give the original number when multiplied together.
This is also the condition for any two factors to make a factor pair; if they produce the given number when multiplied, they make a factor pair; if they don’t, then they are just any two random factors.
To apply this definition, let us look at the factors of 105:
Factors of 105 = 1, 3, 5, 7, 15, 21, 35, and 105
Among these factors, not any two factors make a factor pair; for example, let us take 5 and 7:
5 x 7 = 35
Notice that the product of 5 and 7 is not 105. Therefore 5 and 7 will not make a factor pair. Now let us look at 5 and 21:
5 x 21 = 105
The product of 5 and 21 gives 105. Therefore 5 and 21 are a factor pair of 105. On the same condition, the following are the factor pairs of 105:
Factor pairs of 105 = (1, 105), (3, 35), (5, 21), (7, 15)
Factor pairs can be positive and negative; the pairs mentioned above are positive according to the convention that we ignore the positive (+) sign when writing positive integers. So the positive factor pairs of 105 are:
Positive factor pairs of 105 = (1, 105), (3, 35), (5, 21), (7, 15)
But factor pairs are also negative, which are essentially positive factor pairs but with a negative (-) sign. So these are:
Negative Factor pairs of 105 = (-1, -105), (-3, -35), (-5, -21), (-7, -15)
Factors of 105 Solved Examples
Now that we have thoroughly looked at theoretical mathematics let us apply our knowledge to a more practical side. We will be using examples in this section to demonstrate how each method can be applied to mathematical problems of factors of 105.
Example 1
Use the division method to find out the factors of 105. Also, explain the difference between the division and prime factorization methods.
Solution
The division method depends on the simple division of the given number by another number that divides it ultimately. If the division is complete, then both the divisor and quotient are factors.
Complete division implies a zero remainder produced as a result of that division. The division method to find out factors of 105 is given below:
Let us start with the division of 105 by two and proceed accordingly
\[ \frac{105}{ 2} = 52.5 \]
52.5 is not a whole number; therefore, 2 is not a factor of 105. Let us try the next integer in line: 3
\[ \frac{105}{ 3} = 35 \]
35 is a whole number; therefore, both 3 and 35 are factors of 105; let us try the next number, 4.
\[ \frac{105 }{4} = 26.25\]
26.25 is not a whole number; therefore, 4 is not a factor of 105. We will now look at the next number in line after four which is 5.
\[\frac{105}{ 5} = 21 \]
As 21 is a whole number, therefore 5 is a factor of 105 along with 21. We will skip six and move on to 7.
\[ \frac{105}{ 7} = 15 \]
As 15 is a whole number and we have obtained zero remainders, 7 is a factor of 105 along with 15.
\[\frac{105}{105} = 1 \]
These also divide the number completely; therefore, 1 and 105 both are factors of 105.
From the above steps, we can look and deduce that the factors of 105 are 1, 3, 5, 7, 15, 21, 35, and 105. The total number of factors is 9 of 105.
Total factors of 105 through the division method are:
Factors of 105 = 1, 3, 5, 7, 15, 21, 35, and 105.
Now that we have calculated the factors of 105, we will look at the other section of the question. The difference between the division method and the prime factorization method can be understood from this example.
In the division method, we divide the number with composites and prime numbers, but in the prime factorization method, we only divide from prime numbers. Secondly, in the division, we look for a zero remainder, whereas in prime factorization, we look for the final answer, 1.
Example 2
List down the factors of 105 and also find out the average of its factors.
Solution
From the above example, we found the eight different factors of 105 through the division method; these factors are:
Factors of 105 = 1, 3, 5, 7, 15, 21, 35, and 105.
Once we have found out the factors of 105, let us look at the formula for calculating the average of 105. Average is basically the sum of all factors of 105 divided by the total number of factors which is 8.
Average = Sum of all the factors of 105 / Total number of factors
Average = (1 + 3 + 5 + 7 + 15 + 21 + 35 + 105) / 8
Average = 192 / 8
Average = 24
This is the average of all the factors of 105, and the average is equal to 24.
Hence, the average of all the factors of 105 is 24.
All images/mathematical drawings are created with GeoGebra.
