JUMP TO TOPIC
Factors of 11: Prime Factorization, Methods, Tree, And Examples
The Factors of 11 can be classified as those numbers that result in the number 11 when they undergo multiplication. Such numbers form a factor pair with one another.
Figure 1 – All possible Factors of 11
What Are the Factors of 11?
The factors of 11 are the numbers 1 and 11. Since 11 is a prime number, its two factors are also prime numbers.Therefore, in conclusion, the number 11 has 2 factors. These 2 factors can be grouped together to form a single factor pair. These factors can be negative as well as positive.How To Calculate the Factors of 11?
You can calculate the factors of 11 through various mathematical procedures, but the division method is one of the most accurate and straightforward method. So let’s dive right into the division method for determining the factors of 11.In the division method, the numbers whose factors are to be determined act as the dividend, whereas all the possible numbers which can be qualified as the factors act as the divisors. The respective dividend and the divisors then undergo the division process. After the division process, if the potential divisor produces a whole number quotient along with zero as the remainder, then that divisor is qualified to be a factor for that number.As the number 11 is a prime number, this number’s factors will also be prime numbers. For any prime number, there are 2 factors – one the smallest factor 1 and the other the number itself. Let’s take a look at the division shown below:\[ \frac{11}{1} = 11\]As a whole number quotient 11 is produced, this indicates that the number 1 is a factor of 11. Now let’s look at the division of 11 from the number 11 itself.\[ \frac{11}{11} = 1 \]Again a whole number quotient is produced, so the number 11 also qualifies as a factor of 11. The total number of factors of 11 is 2, and these are given below:Factors of 11: 1 and 11It is not necessary for the factors of a number to be only positive. These factors can be negative as well. A negative sign accompanies the negative factors. The negative factors of 11 are given below:Negative Factors of 11: -1 and -11Factors of 11 by Prime Factorization
Prime factorization is one technique used to determine the factors of a number, prime factors to be exact. Prime factors are those numbers that act as the factors for a given number and are also prime numbers.The prime factorization method is based on the division operation. The division begins with the number itself, and various prime numbers, which are susceptible to being prime factors, act as the divisors.The whole number quotient produced as the result of the division then acts as the dividend in the next step. This entire process is repeated again and again until the number 1 is obtained at the end.The prime factorization for the number 11 is shown below:Prime Factorization of 11 = 1 x 11
The prime factorization for the number 11 is also given below in figure 2: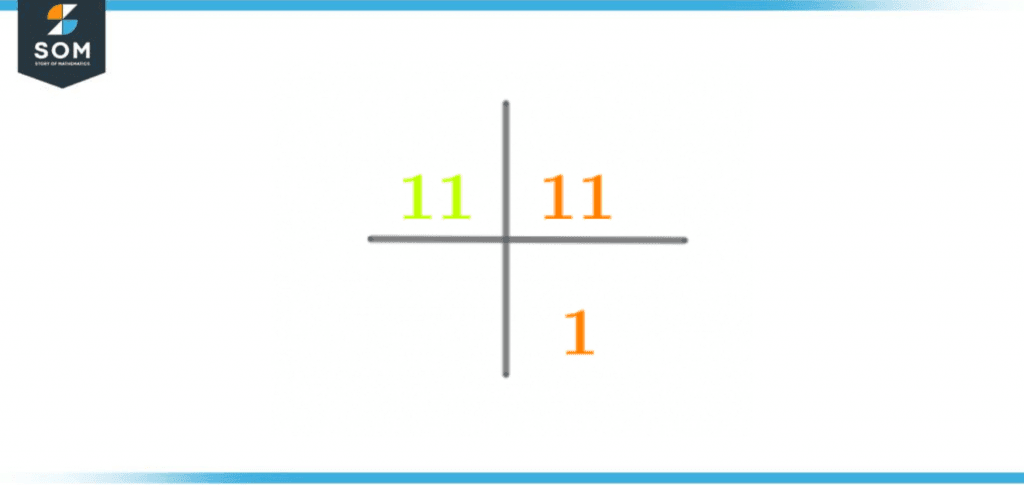
Figure 2 – Prime Factorization of 11
Factor Tree of 11
The prime factorization for a number can also be presented in the form of a factor tree. The factor tree is one of the techniques which is used to determine the prime factors. In a factor tree, one branch will only hold the prime numbers.The factor tree starts with the number itself, and just like prime factorization, this number undergoes division with a prime number. As a result of the division, one branch will hold a prime factor, and the other branch will hold the whole number quotient.The difference between prime factorization and the factor tree is that prime factorization comes to an end at the number 1, whereas the factor tree comes to an end at prime numbers.The factor tree for the number 11 is shown below in the figure: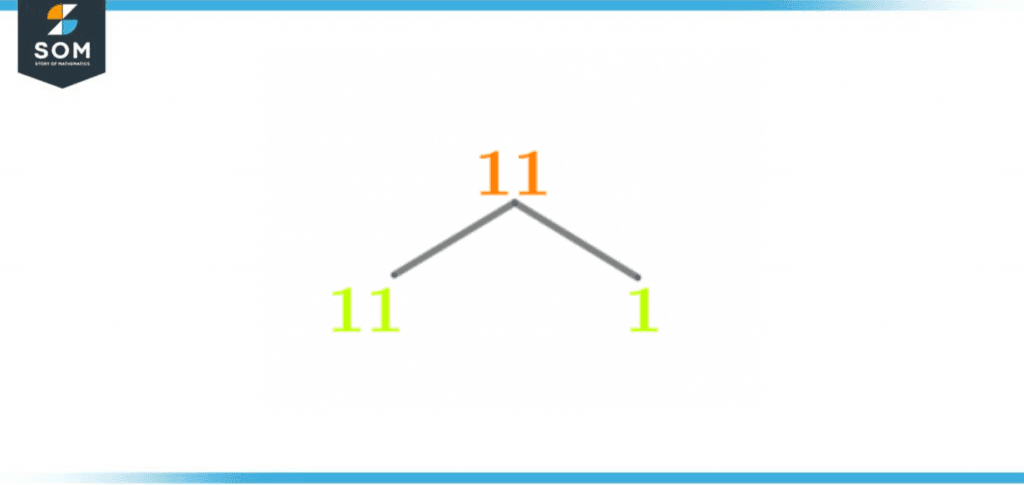
Figure 3 – Factor Tree of 11
Factors of 11 in Pairs
As mentioned above, the factors of 11 can also be classified as those numbers that produce 11 as the product when multiplied together. These two numbers form a factor pair. Within a factor pair, two numbers exist. The condition for a factor pair is that these two numbers must always produce the original number as the result of their multiplication.As the number 11 is a prime number and consists of only two factors, these two factors can formulate a single factor pair. This factor pair is given below:1 x 11 = 11
Factor Pair of 11 = (1, 11)As the factors of a number can also be negative, the same goes for the factor pairs. The requirement for a factor pair of negative numbers is that both the numbers are required to have a negative sign so their multiplication can yield a positive product.The negative factor pair is shown below:-1 x -11 = 11
Negative Factor Pair of 11 = (-1, -11)Some interesting facts about the number 11 are given below:- The number 11 is an odd number, but the sum of the digits of the number 11 produces an even number: 1 + 1 = 2
- In the series of prime numbers, the number 11 is the smallest two-digit prime number.
- 11 is one of the only prime numbers that remains the same when written in reverse.
- The number 11 is also one of the few numbers which remain the same when it is inverted upside down.
Factors of 11 Solved Examples
To further enhance our learning of the factors of 11, let’s take a look at a few solved examples given below, which incorporate the factors of 11.Example 1
Determine the difference between the sum and the difference of the factors of 11. Find out the category of numbers to which the resulting number belongs to.Solution
To begin with, the solution of this example, let’s first list down the factors of 11. These are given below:Factors of 11 = 1 and 11Now, we need two things – the sum and the difference of the factors of 11. Let’s first calculate the sum of the factors of 11. The sum is given below:Sum of factors of 11 = 1 + 11Sum of factors of 11 = 12Now, let’s calculate the next thing, which is the difference. The difference between the factors of 11 is given below:Difference of factors of 11 = 11 – 1
Difference of factors of 11 = 10
Now, let’s calculate the difference between these two quantities as shown below:Difference = Sum of factors of 11 – Difference of factors of 11
Difference = 12 – 10
Difference = 2
The resulting number obtained is the number 2. The category of numbers to which this number belongs to is the set of prime numbers. Moreover, 2 is an even number, so it also belongs to the category of even numbers.Example 2
Determine the average of the factors of 11.Solution
Before moving on to the solution of this example, let’s first take a look at the factors of 11. These are given below:Factors of 11 = 1 and 11The formula for average is given below:\[ Average = \frac{\text{Sum of factors of 11}}{\text{Total Number of factors of 11}} \]Inserting the values within the formula of average:\[ Average = \frac{1 + 11}{2} \]\[ Average = \frac{12}{2} \]Average = 6
Hence, the average of the factors of 11 is 6. All images/mathematical drawings are created with GeoGebra.