JUMP TO TOPIC
Factors of 112: Prime Factorization, Methods, Tree, And Examples
Any number can be divided into its prime factors and composite factors that yield the original number upon multiplication with each other. For the number 112, these factors are all the numbers that give a zero remainder upon division.
Figure 1 – All possible Factors of 112
What Are the Factors of 112?
Factors of 112 are the following: 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112. As 112 is a composite number, hence it has multiple factors.The number 112 has, in total, a set of 10 factors, and these 10 factors can be split into 5-factor pairs accordingly. These are both positive and negative.How To Calculate the Factors of 112?
There are quite a few techniques to calculate the factors of 112, and finding factors is infinitely simpler when we use the division method. There are simple and complex methods available. For prime numbers, finding factors is a piece of cake, but numbers like 112 are composite numbers that have several factors. A simple yet accurate method of division is an approach to finding factors by division until a zero remainder is obtained. Any number that produces a remainder equivalent to zero is a factor according to this method. The quotient which gives the zero remainder is also a factor.Let us apply this definition to our case of number 112 and calculate its factors:\[ \frac{112}{ 2} = 56 \ (factor) \]\[ \frac{112}{3} = 37.3 \ (\text{Not a factor}) \]\[ \frac{112}{ 4} = 28 \ (factor)\]\[ \frac{112}{ 5} = 22.4\ (\text{Not a factor}) \]\[ \frac{112}{7 }= 16 \ (factor)\]\[ \frac{112}{ 8} = 14 \ (factor)\]\[ \frac{112}{112} = 1 \ (factor)\]Looking at the operations above, we can see that numbers like 5 and 3 yield a decimal number, which negates the condition of a factor. Hence they are not factors of 112. Meanwhile, 2, 4, 7, 8, 14, 16, 28, and 56 are factors. All numbers have 1 and the number itself as factors as well. So the factors of 112 according to the division method are:The factors of 112 = 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112Using the division method, we have estimated the above-mentioned factors of 112.Factors of 112 by Prime Factorization
Prime Factorization is a division-based method performed only through prime numbers. The operation is continued until the answer of 1 is obtained. Using this method, we find the prime numbers which will give the original number upon multiplication. Another property of these prime numbers is that if we divide them from the number, the remainder will always be zero.Let us delve deeper into the example of our number 112:Prime Factorization of 112 = 2 x 2 x 2 x 2 x 7
ORPrime Factorization of 112 = $2^{4}$ x 7
The prime factorization of 112 is also shown below: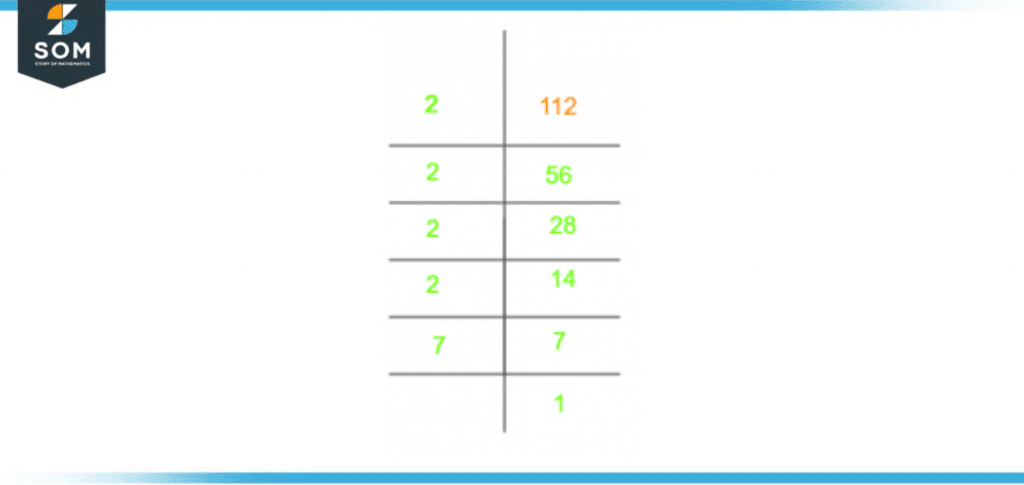
Figure 2 – Prime Factorization of 112
Factor Tree of 112
A factor tree is a visual method for determining factors of any number. There are several mathematical methods to find out the factors of a number, but for a more comprehensive understanding, visual learning is extremely important as well. What differentiates it from other methods is not only the visual element but also the fact that it divides the number into prime factors. Prime factors are basically the factors that are prime numbers. It means that these factors are not divisible by any other number except 1 and the number itself.The visual representation works through the diagram of a tree. The tree starts from the original number and divides into branches representing the numbers after division. This branching of the tree stops once prime numbers are reached. These prime numbers are located at the roots or the ends of the factor tree.For the factor tree of 112, the initial branches will extend out from 112 and will continue till prime factors are obtained at the end. The factor tree for the number 112 is shown below in figure 2: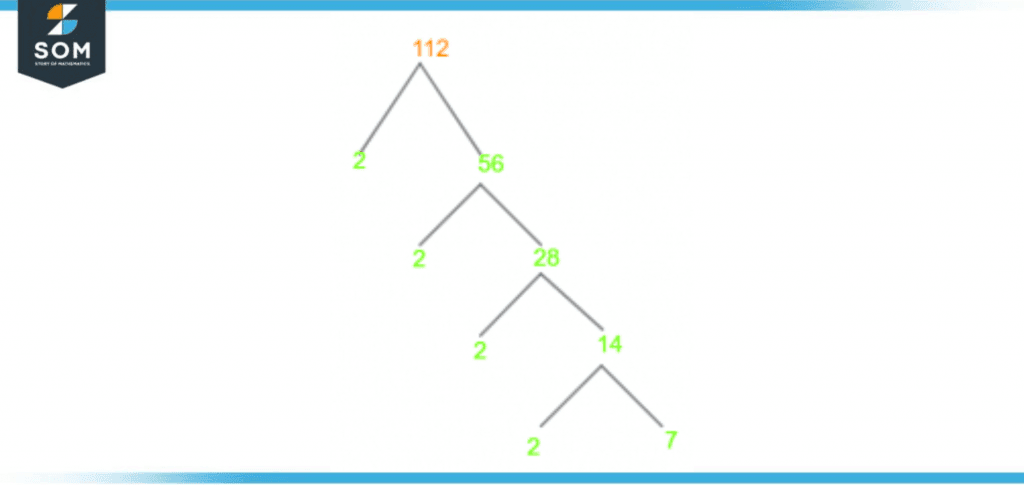
Figure 3 – Factor Tree of 112
Factors of 112 in Pairs
Factor pairs once multiplied by each other give the original number. This property of factors is quite intuitive to understand, any two factors of a number that produce the original number upon multiplication is a factor pair. The necessary condition for two factors to be a factor pair is the multiplication result equivalent to the original number. Looking at our example, the factors of 112 are:Factors of 112 = 1, 2, 4, 7, 8, 14, 16, 28, 56, 112We take any two factors 2 and 7 and multiply them:Product of 2 x 7 = 14
As 14 is not the original number 112, therefore 2 and 7 do not make a factor pair. Similarly, let us take two other factors: 8 and 14Product of 8 x 14 = 112
As the product is 112 hence 8 and 14 make a factor pair. On this note, all the positive factor pairs are:Positive factor pairs of 112 = (1, 112), (2, 56), (4, 28), (7, 16), (8, 14)Factor pairs can also be negative, the negative factor pairs of 112 are: Negative factor pairs of 112 = (-1, -112), (-2, -56), (-4, -28), (-7, -16), (-8, -14)Looking at the negative factor pairs, one notices that all numbers in a pair need to have a negative sign so their multiplication gives a positive number.Factors of 112 Solved Examples
No knowledge is complete without applying it to practical problems and examples. In this section, we will try to apply the methods learned above to different problems to further enhance our understanding of the topic.Example 1
Calculate the total number of factors of 112 through the division method.Solution
The division method is a technique used to calculate the factors of any number. In order to calculate the factors of any given number all you need to do is divide the number 112 until a zero remainder is reached. Any number which gives a zero remainder upon division is a factor of 112 The division of 112 is given as:\[ \frac{112}{2} = 56\]As division by 2 gives a whole number therefore 56 is also a factor along with 2.\[ \frac{112}{ 4} = 28 \]As division by 4 gives a whole number therefore 28 is also a factor along with 4.\[ \frac{112}{7} = 16\]As division by 7 gives a whole number therefore 16 is also a factor along with 7.\[ \frac{112}{8} = 14 \]As division by 8 gives a whole number therefore 14 is also a factor along with 8.This calculation shows that there are several factors of 112. These factors are 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112.Factors of 112 = 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112.
In our case, 112 is a composite number. This means that it has multiple factors other than 1 and the number itself. As prime numbers have only straightforward factors, they make our calculations simpler. But composite numbers require some effort as shown above. As there are several factors, each needs to be verified accordingly but there is nothing to worry about as we have tried to explain it in a simplistic manner. Hence the number 112 has a total of 10 factors: 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112.Example 2
Calculate the average of all the factors of 112.Solution
Before calculating the average of all the factors of 112, it is important to list down the factors. We know it is a composite number that has several factors which are:The factors of 112 are:Factors of 112 = 1, 2, 4, 7, 8, 14, 16, 28, 56, and 112.The sum of these factors is given as:Sum of factors of 112 = 1 + 2 + 4 + 7 + 8 + 14 + 16 + 28 + 56 + 112
Sum of factors of 112 = 248
To calculate the average we need to divide the sum of factors with the total number of factors.The total number of factors of 112 = 10
Average of factors of 112 = 248 / 10
Average of factors of 112 = 24.8
Therefore, the average of the factors of 112 is 24.8