JUMP TO TOPIC
Factors of 12: Prime Factorization, Methods, and Examples
Factors of 12 are the numbers that divide evenly with 12 when all other numbers are divided by 12 up to that number itself.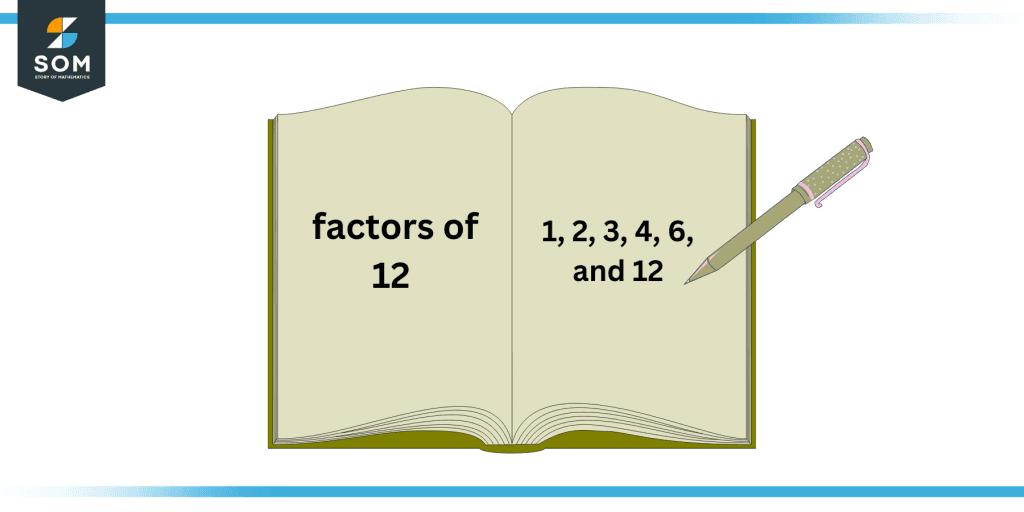
Figure 1 – All possible factors of 12
What Are the Factors of 12?
The factors of 12 are 1, 2, 3, 4, 6, and 12, since all of these divide 12 evenly, leaving no residual.The numbers that divide 12 perfectly without producing a remainder are known as its factors. Being an even composite number, 12, in addition to 1 and 12, has a lot of other factors. The number 12 also has both positive and negative factors.How To Calculate the Factors of 12?
You can calculate the factors of 12 by discovering and compiling a list of all the factors of 12 then examining every number up to and including 12 and determining which numbers produce an even quotient.This approach is really basic and easy. There are only five parts to the complete procedure.First, think about the number 12. Divide it evenly amongst all the numbers from 1 to 12. Record the outcomes. The division produces the following factors:\[ \dfrac{12} {1} = 12\]\[ \dfrac{12} {2} = 6\]\[ \dfrac{12} {3} = 4\]\[ \dfrac{12} {4} = 3\]\[ \dfrac{12} {5} = 2.4 \]\[ \dfrac{12} {6} = 2\]\[ \dfrac{12} {7} = 1.7\]\[ \dfrac{12} {8} = 1.5\]\[ \dfrac{12} {9} = 1.3\]\[ \dfrac{12} {10} = 1.2\]\[ \dfrac{12} {11} = 1.09\]\[ \dfrac{12} {12} = 1 \]Reject the decimals and filter out the positive integer quotient for the aforementioned.Here are the factors of 12: 1, 2, 3, 4, 6, and 12.Negative integers are also included in the factors of 12. The aforementioned procedure must be repeated while taking into account negative numbers to determine how many components in 12 include negative integers.Therefore, all the integers we divided (used as divisors earlier) to arrive at an even number are the positive factors of 12. Here is a list of every positive factor of 12 in ascending order by number: 1, 2, 3, 4, 6, and 12.Negative numbers are included in factors of 12. All of the positive factors of 12 can therefore be changed into negative numbers. Below is a list of the negative factors of 12.Negative factors of 12 are -1, -2, -3, -4, -6, and -12.How Many Factors of 12 Are There?
We discovered that 12 had six positives and six negative factors when we added up the factors we described above. Consequently, there are 12 Factors of 12 in all.Factors of 12 by Prime Factorization
The prime factorization of 12 is given as:2 x 2 x 3
First, keep in mind that all positive integers considered to be prime numbers may only be divided equally by one and by oneself. All prime numbers that when multiplied together, equal 12, are known as prime factors of 12.Prime Factorization of 12 is the process of locating the prime factors of 12. You must divide 12 by the smallest prime number feasible to obtain the prime factors of 12. The next step is to divide the outcome by the smallest prime integer. Continue doing this until you have 1. The arithmetic to demonstrate the factorization of 12 is as follows:\[ \frac{12} {2} = 6\]\[ \frac{6} {2} = 3\]\[ \frac{3} {3} = 1\]Once more, the prime factors of 12 are all the prime numbers you used to divide above.The prime factorization of 12 is shown below in Figure 1: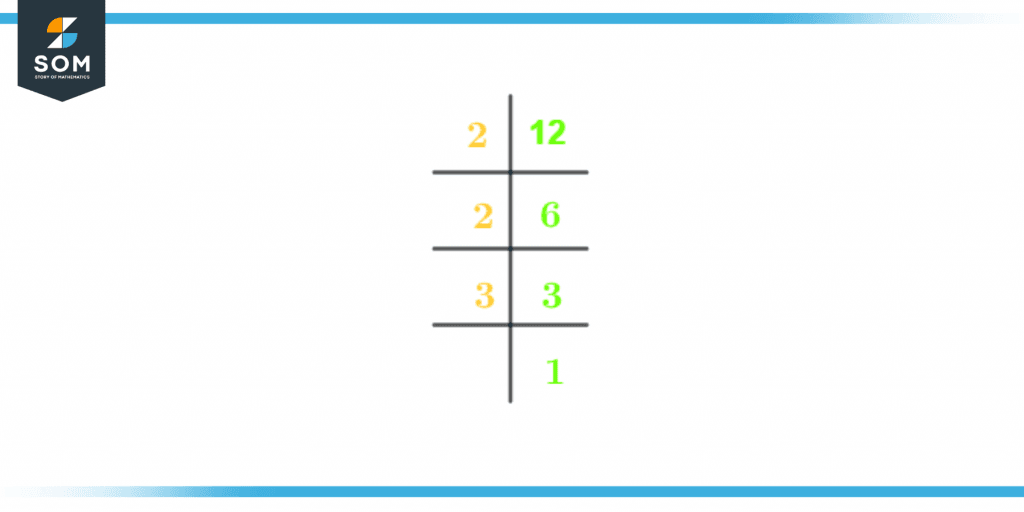
Figure 2 – Prime factorization of 12
How Many Prime Factors Are There in 12?
We discover that 12 has a total of 3 prime factors when we tally the number of prime factors mentioned above.Factor Tree of 12
The factor tree of 12 is given below in Figure 2: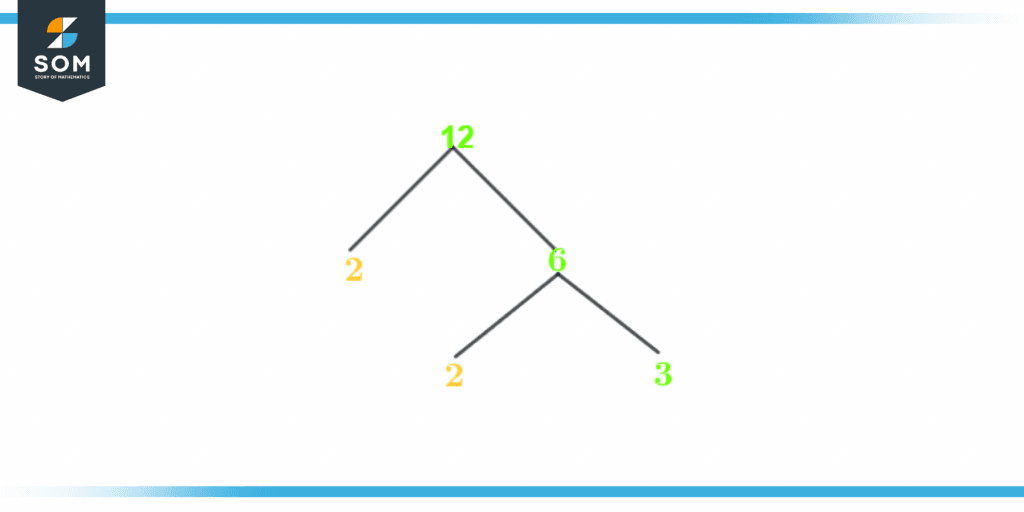
Figure 3 – Factor tree of 12
Factors of 12 in Pairs
A factor pair of 12 consists of two factors that, when multiplied together give 12 as a result. The two integers that can be multiplied together to produce 12 are referred to as the factors, and the number 12 is referred to as the product of these two factors in basic mathematics.We must first obtain all of the factors of 12 before we can calculate the factor pairs of 12. Once you have a list of every one of those factors, you can pair them together to create a list of every pair of factors.As we are aware of every factor that contributes to the number 12, we can utilize this knowledge to determine the factor pairings. To do this, we may search through the list of possible combinations to multiply with each other to find all the possible combinations of 12.12 x 1 = 12
6 x 2 = 12
4 x 3 = 12
3 x 4 = 12
2 x 6 = 12
1 x 12 = 12
Factors of 12 include negative values, as we mentioned earlier. You may convert the list of positive factor pairs above to negative factor pairs of 12 by simply adding a minus sign in front of each factor. Minus times minus becomes positive.The positive pair factors for 12 are (12, 1), (6, 2), and (4, 3).The negative pair factors of 12 are (-12, -1), (-6, -2), and (-4, -3).