JUMP TO TOPIC
Factors of 120: Prime Factorization, Methods, Tree, and Examples
The factors of the number 120 are the integers that produce 120 when multiplied by each other in pairs. In another way, the factors of 120 can be defined as follows:
Figure 1 – All possible Factors of 120
What Are the Factors of 120?
The factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120.120 is an even composite number that has a total of 16 positive factors. All the above-mentioned numbers can be regarded as perfect divisors of 120. When 120 is divided by these three numbers, it is completely divided with zero remainders.How To Calculate the Factors of 120?
There are different ways to find the factors of 120, and one of the methods to find factors of 120 is the factorization by division method.To find the factors of 120 by the division method, start dividing 120 by the smallest natural number that divides 120 completely and proceed with consecutive natural numbers up to the number 120.Divide 120 by the smallest natural number, i.e., 1.\[\dfrac{120}{1} = 120 , r = 0 \]As it has completely divided 120 and the remainder is zero (i.e., r=0), so 1 is a factor of 120.Now, divide 120 by the smallest even prime number, i.e., 2.\[\dfrac{120}{2} = 60 , r = 0 \]As it has again divided 120 completely because a quotient is a whole number, and the remainder is zero. Therefore 2 is a factor of 120.The number 120 can be divided completely by 3 as the cross sum of 120 is 3, which is a divisor by 3 (it is called the divisibility rule of 3). Hence, 3 is also a factor as well as a divisor of 120.\[\dfrac{120}{3} = 40 , r = 0 \]Now apply the Divisibility Rule of 4 to find whether 120 is divisible by 4 if the last two digits of the given number are 0 or form a number that is exactly divisible by 4 as the last two digits form 20, which is divisible by 4. Hence, 120 is also divisible by 4.\[\dfrac{120}{4} = 30 , r = 0 \]Now apply the Divisibility Rule of 5 to check if 5 is a factor of 120. If the last digit of the specified number is 0 or 5, the given number will be divisible by 5. As the last digit of 120 is 0. So it will be divided by 5 completely.\[\dfrac{120}{5} = 24 , r = 0 \]Again apply the Divisibility Rule of 6 to find out if 6 is a factor of 120. If any even number is divisible by 3, the given number will be divisible by 6 also. As 120 is an even number and divisible by 3. Therefore it is also divided by 6.\[\dfrac{120}{6} = 20 , r = 0 \]Now divide 120 by the next natural number, which is 7.\[\dfrac{120}{7} = 17.14, r ≠ 0 \]As 7 has not divided 120 exactly, and the quotient is in a fraction. So, 7 is not a factor of 120.After 7, divide 120 by consecutive natural numbers to find factors of 120.\[\dfrac{120}{8} = 15, r = 0 \]\[\dfrac{120}{10} = 12, r = 0 \]\[\dfrac{120}{12} = 10, r = 0 \]\[\dfrac{120}{15} = 8, r = 0 \]\[\dfrac{120}{20} = 6, r = 0 \]\[\dfrac{120}{24} = 5, r = 0 \]\[\dfrac{120}{30} = 4, r = 0 \]\[\dfrac{120}{40} = 3, r = 0 \]\[\dfrac{120}{60} = 2, r = 0 \]\[\dfrac{120}{120} = 1, r = 0 \]Hence, all the above numbers (i.e., 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, and 120) are factors of 120.Basic Information About Factors
- The divisors of a number that are completely divisible by that particular number are also factors of that number irrespective of prime or composite numbers.
- Factors of 120 can never be in fractions or decimals.
- Factors of 120 can be positive as well as negative.
Factors of 120 by Prime Factorization
When the number 120 is shown in the form of multiplication of all its possible prime factors, it is called the prime factorization of the number 120. The prime factorization method is most commonly used to calculate the factors of a given number.To find factors of 120 by the prime factorization method, divide 120 by the smallest prime number, which divides 120 completely without leaving any remainder. Then again, divide the quotient by the next smallest prime number. This procedure will continue until the quotient becomes 1.Given below is the method to calculate factors of 120 by prime factorization:Firstly, divide 120 by the smallest possible prime number divisor, which is 2.\[\dfrac{120}{2} = 60 \]Secondly, divide the quotient 60 by the smallest possible prime number divisor, which is again 2.\[\dfrac{60}{2} = 30 \]Thirdly, divide the quotient 30 again by 2.\[\dfrac{30}{2} = 15 \]Fourthly, divide 15 by the smallest possible prime factor of 15, which is 3.\[\dfrac{15}{3} = 5 \]At last, the quotient 5 is a prime number and divisible by itself.\[\dfrac{5}{5} = 1 \]Therefore, the prime factorization of 120 can be stated as:Prime Factorization of 120 = 2 × 2 × 2 × 3 × 5The prime factorization of 120 can also be depicted as:120 = 2 x 2 x 2 x 2 x 3 x 5
The prime factorization of 120 is shown in following figure 2: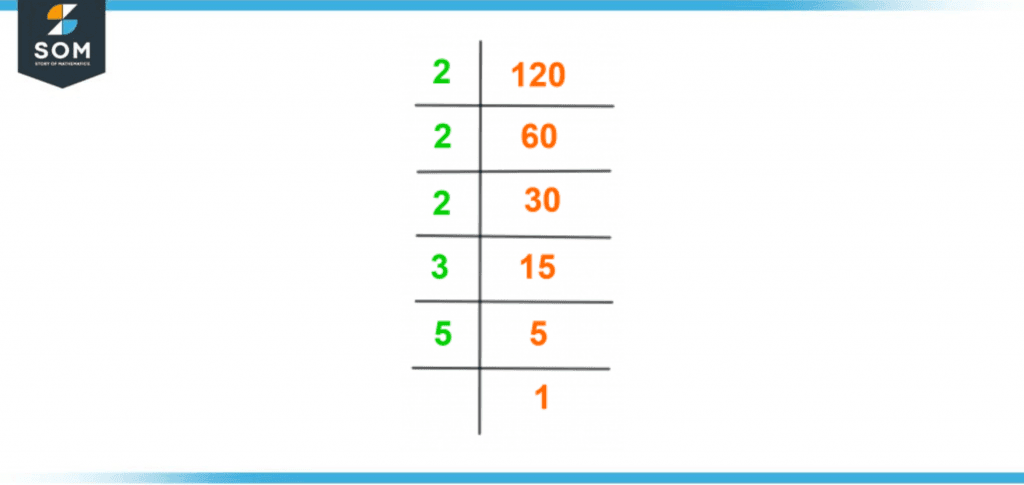
Figure 2 – Prime Factorization of 120
Factor Tree of 120
A factor tree is another way for easy calculation of the factors of a number. Factor trees are specifically used to show the prime factorization of any given number in which each branch of the tree splits into the factors of the given number.The branch of the tree splits into two factors at the end of the branch from which one is a prime factor and the other is a composite factor. Keep dividing the composite number again unless the only two factors remain, that are prime numbers, and the branch will stop.Considering the rules of division by factor tree method, if we write 120 into its multiples, it is shown as;120 = 2 × 60On dividing 60 into its multiples as follows;60 = 2 × 30By splitting 30 into its multiples as shown below;30 = 2 × 15On further dividing 15 into its multiple factors:15 = 3 × 5Here one important thing to note is that the number 15 splits into branches, each with a prime factor. Thus, any further division is not possible, and therefore the factor tree appears as:120 = 2 × 2 × 2 × 3 × 5Factor Tree of 120 can be shown in the following figure 3: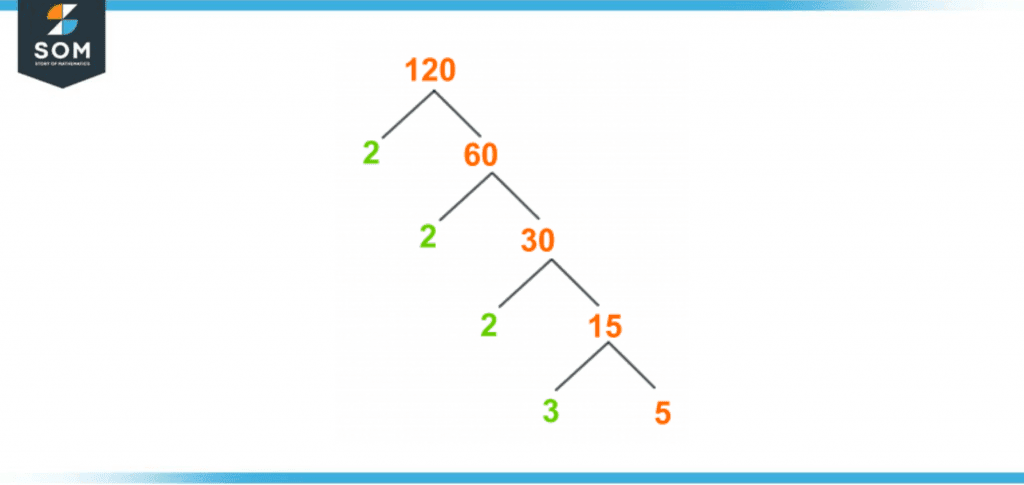
Figure 3 – Factor Tree of 120
Factors of 120 in Pairs
Factors of 120 in pairs are the sets of two integral numbers whose product gives us the number 120 are called factors of 120 in pairs. It can also be explained as the product of the factors of the number 120 represented in the form of pairs or sets.Pair Factors consist of numbers in pairs that are multiplied by each other and give the result of 120. Following are the pair factors of 120.1 × 120 = 1202 × 60 = 1203 × 40 = 1204 × 30 = 1205 × 24 = 1206 × 20 = 1208 × 15 = 12010 × 12 = 120Hence, the factors of 120 can be written in pairs as follows:(1, 120)(2, 60)(3, 40)(4, 30)(5, 24)(6, 20)(8, 15)(10, 12)120 also can have two negative numbers as pair factors. For example:(-2) × (-60) = 120(-5) × (-24) = 120 (-8) × (-15) = 120Hence, the following are some examples of negative pair factors of 120:(-2, -60)(-5, -24)(-8, -15)So it can be derived that the product of all factors of 120 in its negative form gives the result 120. Hence, all are called negative pair factors of 120.Important Facts About 120
- 120 is an even and composite number.
- 120 has only three prime factors.
- 120 has 16 divisors.
- The number 120 is highly composite. It is also called anti-prime
Factors of 120 Solved Examples
Example 1
Express 120 in the form of its prime factorization.Solution
As we know thatPrime Factorization of 120 = 2 × 2 × 2 × 3 × 5So, 120 can be expressed in the form of its prime factorization as follows:120 = 2 x 2 x 2 x 3 x 5
