JUMP TO TOPIC
Factors of 128: Prime Factorization, Methods, Tree, and Examples
All the numbers that entirely divide the number 128, leave zero as the remainder, and give a whole number in the quotient are called the factors of 128.

Figure 1 – All possible Factors of 128
Factors of 128 can also be narrated as the product of two numbers that produce 128 when multiplied by each other.
This article explains the nitty gritty of the factors of 128 and methods to find these factors using different techniques, primarily prime factorization and conventional division methods.
Facts About 128
Following are the basic features of the number 128, which must be recalled to find out the factors of 128.
- 128 is an even number.
- 128 is a composite number.
- 128 is not a perfect square.
- 128 is a deficient number. It is also called an insufficient number. Any number is called a deficient number if the sum of all factors is less than double the said number.
What Are the Factors of 128?
The factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128.
Since 128 is an even as well as a composite number, it has eight positive factors. All the factors of 128 in their negative form are negative factors of 128, which are also 8 in the count for 128. All the above-stated numbers are also divisors of 128 because when the number 128 is divided by the given numbers, it leaves nothing as a remainder. The factors of 128 are integers.
How To Calculate the Factors of 128?
You can calculate the factors of number 128 by using the conventional division method. For this purpose, start dividing 128 by the smallest natural number that divides 128 perfectly without leaving any remainder.
Divide 128 by the smallest natural number, which is 1.
\[ \dfrac{128} {1} = 128, r = 0\]
Since one has wholly divided the dividend 128 without leaving any remainder ( r = 0) and generating a whole number in the quotient, so, 1 is a factor of 128.
Now divide 128 by the following consecutive natural number, i.e.,2, the smallest even prime number.
\[ \dfrac{128} {2} = 64, r = 0\]
128 has been divided completely by its divisor, i.e., 2. Therefore, 2 is also a factor of 128. Now try to divide 128 by the next consecutive natural number, 3 (smallest odd prime number).
\[ \dfrac{128} {3} = 42.37, r ≠ 0\]
Because three has not divided 128 altogether, the quotient is a fraction or decimal. Hence, 3 is not a factor of 128.
For attaining more factors, divide 128 by natural numbers that completely divide 128 and leave zero remainders as shown below:
\[ \dfrac{128} {4} = 32, r = 0\]
\[ \dfrac{128} {8} = 16, r = 0\]
\[ \dfrac{128} {16} = 8, r = 0\]
\[ \dfrac{128} {32} = 4, r = 0\]
\[ \dfrac{128} {64} = 2, r = 0\]
\[ \dfrac{128} {128} = 1, r = 0\]
It is evident from the division that the number 128 has eight factors in total. These numbers are regarded as factors of 128 because they leave zero remainders when divided by 128. Therefore, all the numbers 1, 2, 4, 8, 16, 32, 64, and 128 are factors of 128.
Salient Features of Factors of 128
Following are some features of the factors:
- The number 1 is the minor factor of 128 as it is the factor of every number.
- The number 128 cannot have any factor which is larger than itself. Hence 128 is the largest factor of the number 128.
- 128 has only one odd factor, which is also 1.
- Except for 1, all the other factors of 128 are even numbers.
- The number 128 has only one prime factor, i.e., 2.
- For number 128, the sum of factors is 255.
Factors of 128 by Prime Factorization
The depiction of the number 128 as a product of each of its prime factors is called prime factorization of the number 128. Prime factorization is one of the vital methods that can be utilized to calculate the factors of 128.
To get the objective, divide 128 by the smallest prime number, which divides 128 without any remainder. The process continues till one is obtained as the quotient. This simple technique represents the number in terms of its prime factors.
Below are the steps to calculate factors of 128 using the prime factorization technique.
Firstly divide 128 by the smallest prime number. The smallest prime number is 2 which is divisible by 128, as shown below:
\[ \dfrac{128} {2} = 64 \]
As the number resulting in the quotient is 64, which is not a prime number, it can further be divided by the smallest prime number again.
\[ \dfrac{64} {2} = 32 \]
The quotient 32 can again be divided by 2.
\[ \dfrac{32} {2} = 16 \]
The resulting number 16 can also be divided further by 2.
\[ \dfrac{16} {2} = 8 \]
The number 8 is further divided as follows.
\[ \dfrac{8} {2} = 4 \]
The division continues until we get a prime number. Hence it will go further as follows:
\[ \dfrac{4} {2} = 2 \]
Since 2 is a prime number and it can be further divided by itself only.
\[ \dfrac{2} {2} = 1 \]
The quotient 1 cannot be divided any further.
Therefore, the prime factorization of 128 can be expressed as follows:
Prime Factorization of 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
128 can also be detonated in the form of its prime factors as:
128 = 2$^7$
The prime factorization of 128 is also shown in following figure 2.
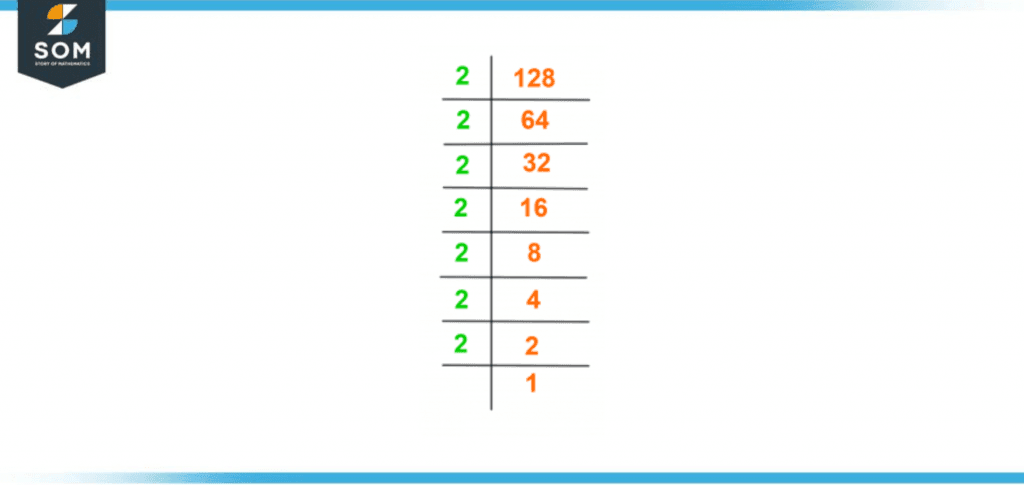
Figure 2 – Prime Factorization of 128
Factor Tree of 128
A factor tree is a different way of determining the factors of 128. A factor Tree is a photographic representation where the prime factorization of the number 128 is established in the form of a tree, and the branches contain the factors of number 128.
The factor tree continues to split till further division is not possible. It generates prime numbers and composite numbers at each level of division. The composite number again undergoes further division producing a prime number. Once both numbers are prime, the factor tree will stop.
For the given number, considering the rules of division by the factor tree method, If we write 128 into multiples, it would be;
128 = 2 x 64
Split 64 into multiples, it would be;
64 = 2 x 32
Repeat the procedure unless both prime numbers appear in the split.
32= 2 x 16
16 = 2 x 8
8 = 2 x 4
4= 2 x 2
It is necessary to note here that the number 4 has given prime numbers on both of the branches. Therefore, it cannot be divided into its further branches; the factor tree of 128 appears as following figure 3.
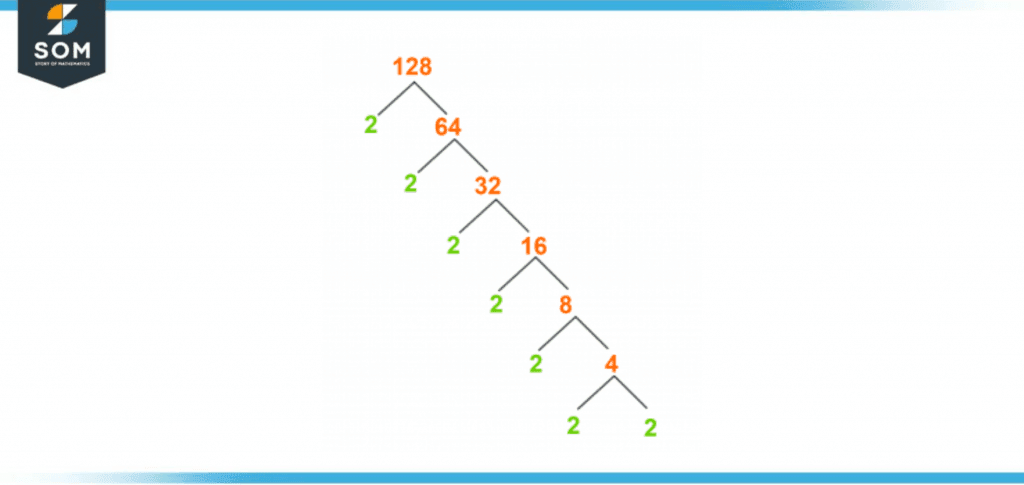
Figure 3 – Factor Tree of 128
Factors of 128 in Pairs
A set of two natural numbers, which are multiplied to produce the number 128, are called factors of 128 in pairs.
In another way, it is stated as the product of the factors of the number 128 in the form of pairs.
1 x 128 = 128
2 x 64 = 128
4 x 32 = 128
8 x 16 = 128
The number 128 has a total of 8 factors which can be written in pairs as below:
(1, 128)
(2, 64)
(4, 32)
(8, 16)
As the multiplication of two negative numbers always generates a resulting positive number. Therefore, when multiplied, all the pair factors of 128 in negative form result in a positive 128. Hence, the following are also pair factors of 128.
(-1) x (-128) = 128
(-2) x (-64) = 128
(-4) x (-32) = 128
(-8) x (-16) = 128
The negative pair factors of number 128 are given as follows:
(-1, -128)
(-2, -64)
(-4, -32)
(-8, -16)
Tips and Tricks
- Factors of any number can only be integers and whole numbers.
- Decimals and fractions are never the factors of any number.
- A number can also have negative factors. The negative factors are similar to positive factors. Negative factors are written with a negative sign.
Factors of 128 Solved Examples
Example 1
Ana has been given a home task to write down the techniques to find the factors of 128. Please help her to write down different methods.
Solution
Julia can find the factors of 128 using the following different methods.
- Factors of 128 by Division Method.
- Factors of 128 by Multiplication Method.
- Factors of 128 by Prime Factorization Method.
- Factors of 128 by Factor Tree Method.
Example 2
Peter has been tasked to find whether 128 is a deficient number or not. How will he find it?
Solution
Peter knows that a number n is deficient when the sum of all the factors/divisors is less than double the number (2n).
Factors of 128 are 1, 2, 4, 8, 16, 32, 64, and 128.
Sum of factors of 128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128
Sum of factors of 128 = 255
Double of 128 = 2n
2n = 256
The sum of all divisors, i.e., 255, is less than (2n =256 ). Hence, 128 is a deficient number.
Images/mathematical drawings are created with GeoGebra.
