JUMP TO TOPIC
Factors of 135: Prime Factorization, Methods, Tree, and Examples
The factors of 135 are a list of numbers that divide it ultimately. When we talk about complete division, the elements divide the number so that no remainder is produced. Similarly, no remainder is produced, implying that a quotient is always a whole number with no decimal part.

Figure 1 – All possible Factors of 135
When we talk about even or odd numbers, 135 identifies as an odd number because the last digit is an odd number. Even or odd numbers can be determined by looking at their previous digit. If the last digit is 0, 2, 4, 6, 8, then the number is even. 1, 3, 5, 7, 9 implies that it is odd.
The next question is finding these factors and methods to achieve this solution. The methods discussed in this article are the prime factorization method, the division technique, and drawing a factor tree figure.
All are essential for understanding the concept of factorization. In this article, we will explore these concepts in detail.
What Are the Factors of 135?
The factors of 135 are 1, 3, 5, 9, 15, 27, 45, and 135.
135, as we can see, is not a prime number. 135 is classified as a composite number due to its divisibility with more than two factors: 1 and 135. The fact that it ends with a ‘5’ means that it must be divisible by 5, which also makes it a factor.
How To Calculate the Factors of 135?
You can calculate the factors of 135 using the division method, which is the most traditional and intuitive method of finding the factors of any number. The division method is simple yet it gives pretty accurate answers. The process is based on the mathematical operation of division.
In the division method, we know that all numbers are divisible by 1, so we ignore that and start from 2. Now, if a number is even, we can assume 2 as the first factor, but if the number is odd, we ignore 2 and jump to the next integer, 3.
We keep on doing that until all factors are confirmed. This method has been shown below:
\[ \frac{35 }{ 3} = 45 \]
The division of 135 by 3 has given a quotient with no decimal part; the absence of this decimal part means that 3 has divided 135 completely.
\[ \frac{135}{ 4} = 33.75 \]
The quotient here is not a whole number; this means that 4 did not divide 135 completely. Hence 4 is not a factor of 135. Similarly, we try for other integers to find out the factors of 135.
\[ \frac{135}{ 5} = 27\]
\[ \frac{135 }{9 }= 15\]
\[ \frac{135}{ 15 }= 9\]
\[ \frac{135 }{ 27 }= 5 \]
\[ \frac{135}{ 45} = 3 \]
\[ \frac{135}{ 135} = 1 \]
\[ \frac{135 }{ 1} = 135 \]
The divisors shown above are the factors of 135. We found these factors using the division method, which has allowed us to find out the entire list of factors of 135:
Factors of 135 through division method: 1, 3, 5, 9, 15, 27, 45, and 135.
Factors of 135 by Prime Factorization
Prime factorization of 135 is a technique for finding out the prime factors of 135. Now 135 has both prime and composite factors, but through this method, we can represent 135 by multiplying a few specific prime numbers.
Prime factors are prime numbers. It must be noted that not all prime numbers can make prime factors. The prime numbers which divide 135 ultimately or evenly will be considered factors of 135. These factors, which have been obtained through the division by prime numbers, are called prime factors.
Prime factorization is based on the division method which we studied above. However, it is differentiated from it because the quotient produced in each step acts as the dividend for the next step of prime factorization.
How it is used for this specific method has been shown below:
135 $\div$ 3 = 45
45 $\div$ 3 = 15
We can see that 45 is now the dividend; the same happens in all steps.
15 $\div$ 3 = 5
5 $\div$ 5 = 1
Using the prime factorization method, we have found the following prime factors of 135. The prime factors of 135 are 3, 3, 3, and 5.
Prime factorization of 135 = 3 x 3 x 3 x 5
The prime factorization of 135 is shown below in figure 2:
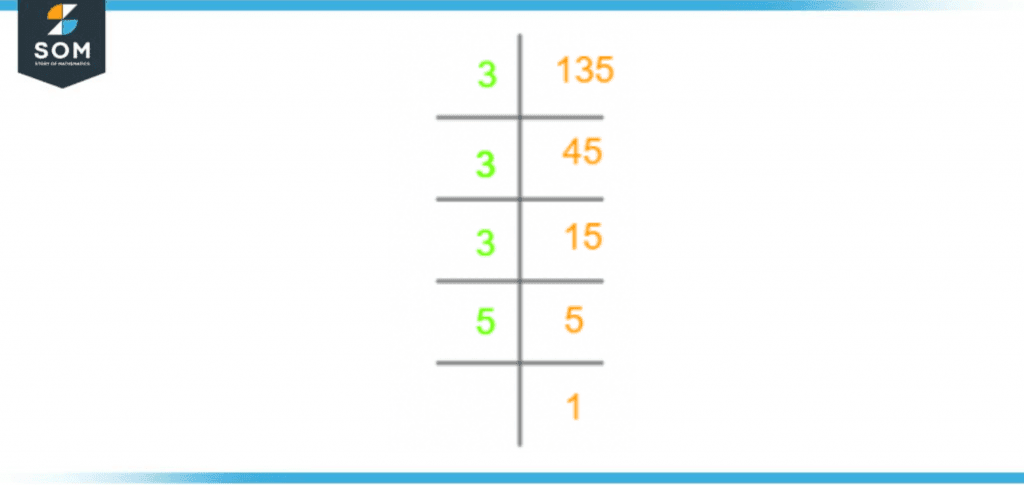
Figure 2 – Prime Factorization of 135
Factor Tree of 135
The factor tree representation is a way of expressing a number’s factors in a more detailed and comprehensive manner. Once we have calculated the prime factors using that method, we can represent them on a tree using this diagram.
What makes factor trees different from other methods is that they use visual learning aids. Just as Venn diagrams can help us improve our understanding of set and set theory, factor trees can help us boost our comprehension of factorization and finding factors of any number.
Building on the shape of a tree, for a factor tree of 135, we write down 135 and extend two branches out of it. The divisor and quotient will be written on each branch.
This is continued until there is no further division possible. This has been elaborated in Figure 3 attached for further comprehension:
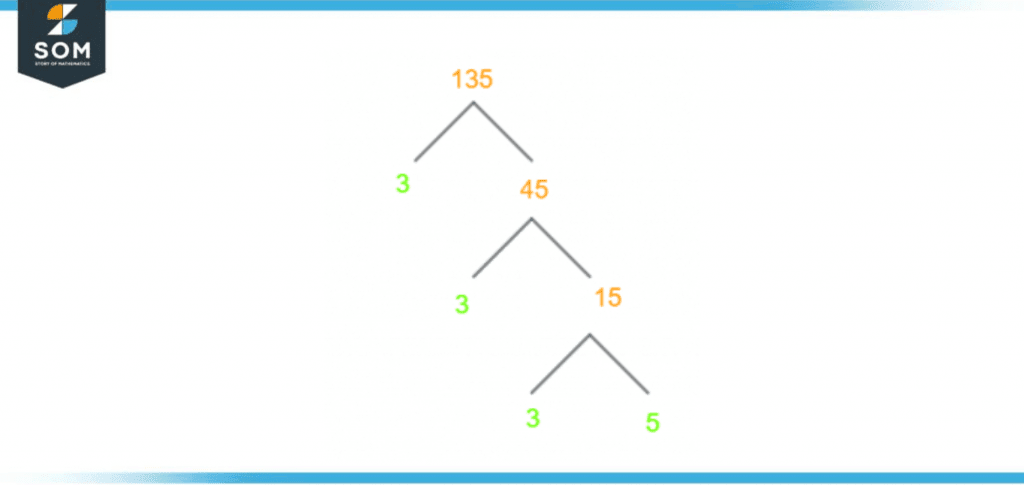
Figure 3 – Factor Tree of 135
Factors of 135 in Pairs
The factor pairs of 135 are particular pairs from among the factors of this number. What makes these pairs unique is that when they are multiplied together, they will always give the original number as a result. Not all pairs from the factor list can be factor pairs.
The necessary condition for any two factors to make a pair is that they must give the original number when they are multiplied together. We can not randomly pick up two factors and call them a factor pair. It is possible only if they satisfy the condition mentioned above.
To find out the factor pairs of 135, let us first revisit the factors of 135:
Factors of 135 = 1, 3, 5, 9, 15, 27, 45, and 135.
135 has a total of 8 factors which means that we can expect 4-factor pairs. The factor pairs of 135 based on the condition mentioned above are:
Factor pairs of 135 = (1, 135), (3, 45), (5, 27), (9, 15)
These are the factor pairs of 135. The factor pairs can either be positive or negative. The positive factor pairs are the same as the ones mentioned earlier:
Positive factor pairs of 135 = (1, 135), (3, 45), (5, 27), (9, 15)
The negative factor pairs only include a negative (-) before every number; therefore, the negative factor pairs are:
Negative factor pairs of 135 = (-1, -135), (-3, -45), (-5, -27), (-9, -15)
Factors of 135 Solved Examples
Let us look at the examples of 135 to understand the theory better.
Example 1
List down the factors of 135 and separate the even and odd factors from among them.
Solution
The factors of 135 through the division method are:
Factors of 135 through division method = 1, 3, 5, 9, 15, 27, 45, and 135
Looking at the list of factors of 135, we can observe that there are no even factors among them. This means that 135 only has odd factors. These odd factors are: 1, 3, 5, 9, 15, 27, 45, and 135. Therefore:
Even factors of 135 = none
Odd factors of 135 = 1, 3, 5, 9, 15, 27, 45, and 135.
Example 2
Find out the common factors that exist between 135 and 35.
Solution
To find out the common factors between 135 and 35, we need first to find out the factors of both. We already know the factors of 135, which are:
Factors of 135 = 1, 3, 5, 9, 15, 27, 45, and 135.
So we need to find the factors of 35 through the division method:
\[ \frac{35{ 5} = 7 \]
\[ \frac{35}{ 7} = 5 \]
\[ \frac{35}{ 35} = 1 \]
\[ \frac{35 }{1 }= 35 \]
So the factors of 35 are:
Factors of 35 = 1, 5, 7, and 35
Now to find out the common factors between 135 and 35, we look at the factors of both. We can observe that the common factors are: 1 and 5.
Therefore, the common factors between 135 and 35 are = 1 and 5.
All images/mathematical drawings are created with GeoGebra.
