JUMP TO TOPIC
Factors of 130: Prime Factorization, Methods, Tree, And Examples
Factors of 130 are the numbers that when divided by 130, give zero as the reminder. Factors of the number are also called divisors. Every number has both positive and negative factors, but we usually don’t take negative factors into account.
Figure 1 – All possible factors of 130
In total, there are 8 factors of the number 130, and if we consider all the negative factors too, then the total number of factors will be 16.What Are the Factors of 130?
The factors of 130 are 1, 2, 5, 10, 13, 26, 65, and 130. All these numbers are factors of 130 as they leave zero remainders when divided by 130.When you multiply the two whole numbers and get 130 as an answer, then you can say that those two numbers are the factors of 130. Similarly, when any whole number is divided by 130 and gives zero as the remainder, then that number can be regarded as the factor of 130.How To Calculate the Factors of 130?
To find the factors of 130, we will choose the smallest number i.e. 1, and divide it by the number itself. If the answer gives zero as the remainder, then 1 is a factor of 130. The fun fact here is that 1 is the factor of every number.The factors can be found as:\[ \dfrac{130}{1} = 130,\ r = 0 \]This can also be confirmed by the multiplication method as when 1 and 130 are multiplied, the product is 130, which means that 1 and 130 are the factors of 130.This can be shown as:1 x 130 =130
Now, let’s continue checking for other whole numbers such as 2:\[ \dfrac{130}{2} = 65\ ,\ r = 0 \]So, 2 and 65 are the factor of 130.Confirming via multiplication method as well.2 x 65 = 130
So, 2 and 65 are also factors.Other factors can also be checked using the same method.The factors of 130 by division method are given as:\[ \dfrac{130}{1} = 130 \]\[ \dfrac{130}{2} = 65 \]\[ \dfrac{130}{5} = 26 \]\[ \dfrac{130}{10} = 13 \]\[ \dfrac{130}{13} = 10 \]\[ \dfrac{130}{65} = 2 \]\[ \dfrac{130}{26} = 5 \]\[ \dfrac{130}{130} = 1 \]Therefore, by division method, factors of 130 are 1, 2, 5, 10, 26, 65, and 130.Important Properties
Here are some properties of factors of 130 that must be noted:- Factors of 130 can be calculated using various methods such as the upside-down division method, divisibility test method, multiplication method, and prime factorization.
- The additive inverse of any of the factors of 130 is also its factor.
- The factors of 130 can neither be decimal nor in a fraction.
- 130 is an even number, therefore 2 is the smallest prime factor of 130.
130 x 1 = 130 65 x 2 = 130 26 x 5 = 130 13 x 10 = 130
Therefore, by the above method, the factors of 130 are 1, 2, 5, 10, 26, 65, and 130.We can use this method to find the factors of very large numbers as well.Factors of 130 by Prime Factorization
When two prime numbers are multiplied to give a new number, then those numbers are called Prime Factors of the product. Following are steps that must be followed to find the factors of 130 using prime factorization:Step 1
First, find the smallest factor of the number 130, which is 1.Step 2
Now, determine whether the given number is even or odd. Since 130 is an even number, therefore it is divisible by 2, which means that 2 is also the prime factor of 130.Step 3
Divide 130 by 2, which gives us:\[ \dfrac{130}{2} = 65 \]This means 65 is also the factor of 130.Now for further evaluation, use the quotient 65 and find its prime factors.Step 4
The prime factorization of 65 is given as:\[ \dfrac{65}{5} = 13 \]Therefore, 5 is also the factor of 130.Step 5
Keep repeating the above process until another prime factor is obtained.Now the quotient is 13 which is another prime factor, therefore here you can stop the process as:\[ \dfrac{13}{13} = 1 \]Step 6
The prime factorization of 130 is given as:130 = 2 x 5 x 13
Factor Tree of 130
A factor tree is formed by multiplying all the prime numbers with the results of the number itself. For 130, the factor tree is given as: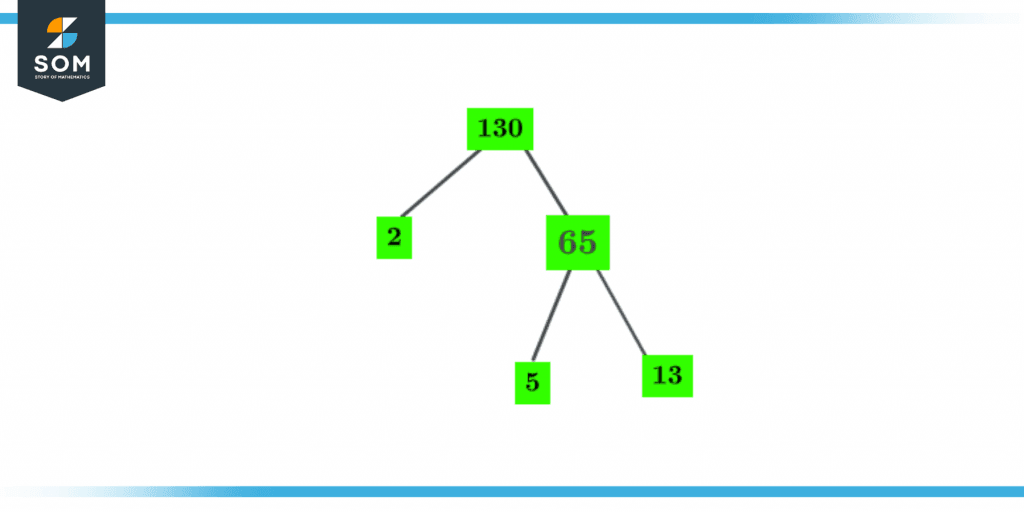
Figure 2 – Factor Tree of the number 130
We can create this factor tree by dividing 130 by the smallest prime number, which is 2. Then we will further divide it until we get a prime number that is not divisible or is 1. We will then multiply all the prime numbers as:1 x 2 x 5 x 13 = 130
Factors of 130 in Pairs
Factor pair of any number can be given by any two whole numbers which multiply to give that specific number.For the number 130, we can calculate the pairs like this:130 ✕ 1 = 130
65 ✕ 2 = 130
26 ✕ 5 = 130
13 ✕ 10 = 130
So this means that 130 has the four-factor pairs including (1,130), (2,65) , (5,26), and (10,13).We can also find the negative pairs of 130, which will be (-1,-130), (-2,-65), (-5,-26), and (-10,-13).Factors of 130 Solved Examples
Let’s solve some examples which involve the factor of 130.Example 1
Steve needs to list the factors of 100 and 130 and find the common factors between them.Solution
The factors of 100 are:Factors: 1, 2, 4, 5, 10, 20, 25, 50, 100 The factors of 130 are:Factors: 1, 2, 5, 10, 13, 26, 65, 130From the above, we can conclude that 1,2, 5, and 10 are the common factors. Hence, the common factors between 100 and 130 are 1,2, 5, and 10.Example 2
What are the negative pair factors of 130?Solution:
The negative pair factors of 130 are given as:-1 x -130 = 130
Hence, (-1,-130), is a negative pair factor of 130.-65 x -2 = 130
Hence, (-2,-65), is a pair factor of 130.-26 x -5 = 130
Hence, (-5,-26), is a pair factor of 130.-13 x -10 = 130
Hence, (-10,-13), is a pair factor of 130.Therefore, the negative pair factors are (-1,-130), (-2,-65), (-5,-26) and (-10,-13).Images/mathematical drawings are created with GeoGebra.