JUMP TO TOPIC
Factors of 14: Prime Factorization, Methods, Tree, And Examples
The Factors of 14 are the numbers that produce 14 as the product when these numbers are multiplied together. The factors of 14 are also the numbers that yield zero as the remainder whenever 14 is divided from these numbers.

Figure 1 – All possible Factors of 14
The factors of the number 14 can be determined through various methods such as the prime factorization method and the division method. Prior to determining the factors, it is necessary to determine the range in which these factors lie.
The range of the factors for any number lies between the smallest factor 1 and half of that number. In the case of the number 14, the half of 14 is 7 so the factors of 14 will lie between 1 and 7.
14 is an even composite number which indicates that it is a multiple of 2 and consists of more than 2 factors.
In this article, we will take a closer look at the factors of 14 and how to determine them. We will also go through the various methods which can be used to determine the factors of 14.
What Are the Factors of 14?
The factors of 14 are 1, 2, 7, and 14. These numbers render zero as the remainder when 14 is divided from them. The smallest factor of 14 is 1 and the largest factor of 14 is 14 itself.
14 is an even composite number so that indicates that the number 2 is also a factor of 14.
How To Calculate the Factors of 14?
You can calculate the factors of 14 through two methods: the division method and the prime factorization method. Let’s first take a look at the division method.
The division method states that a number can only be considered as a factor if it produces zero as the remainder and also gives off a whole number quotient. If these two conditions are met, only then the number can be categorized as a factor.
Since 14 is an even number, so let’s first take a look at its division from 2. The division is given below:
\[\frac{14}{2} = 7\]
This division indicates that zero is produced as the remainder and a whole number quotient 7 is produced so this indicates that 2 is a factor of 14.
Let’s take a look at the divisions of the other factors of 14. First, let’s consider the division of 14 with the smallest factor 1:
\[\frac{14}{1} = 14 \]
Another unique aspect of the division method is that if a factor produces a whole number quotient, then the said quotient is also considered as a factor. Keeping this in mind, let’s consider the division of 14 with 7:
\[\frac{14}{7} = 2\]
Lastly, let’s consider the division of 14 with the greatest factor, which is 14 in this case:
\[\frac{14}{14} = 1\]
Therefore, the factors of 14 are given below:
Factors of 14: 1, 2, 7, and 14
Factors of 14 by Prime Factorization
Prime Factorization is the technique through which the prime factors for any number are determined. The prime factors are the prime numbers which are also the factors for that number.
The condition of prime factorization is that the division is throughout carried out with the help of prime numbers until 1 is obtained at the end.
The prime factorization begins with the number itself and after dividing it from a prime factor, it produces a whole number quotient. This quotient then acts as the dividend and the process is carried out.
The prime factorization of 14 is given below:
14 $\div$ 2 = 7
7 $\div$ 7 = 1
So the prime factorization for 14 can be written as follows:
Prime Factorization of 14 = 2 x 7
The prime factorization of 14 is also shown below in figure 1:
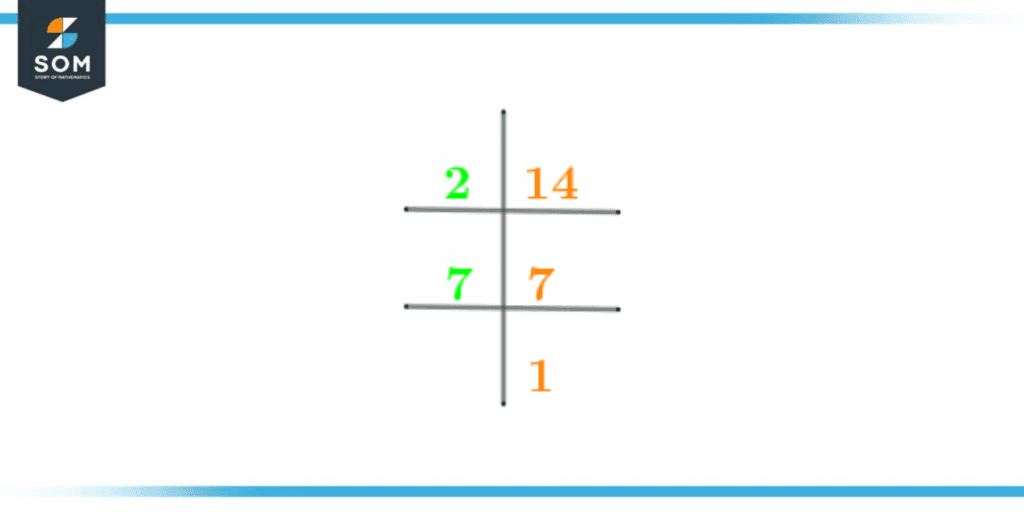
Figure 2 – Prime Factorization of 14
Hence, the number 14 has two prime factors and these are 2 and 7.
Factor Tree of 14
The factor tree is a visual representation of the prime factors of a number. It is a pictorial description of the prime factors of that number.
The factor tree follows the same flow of division as that conducted in the prime factorization method. The only notable difference is that instead of ending at 1, the factor tree ends at the prime factors.
The factor begins with the number and then extends out its branches into a prime factor and a respective whole number quotient. This process continues till prime numbers are obtained at the end.
The factor tree of 14 is shown below in figure 2:
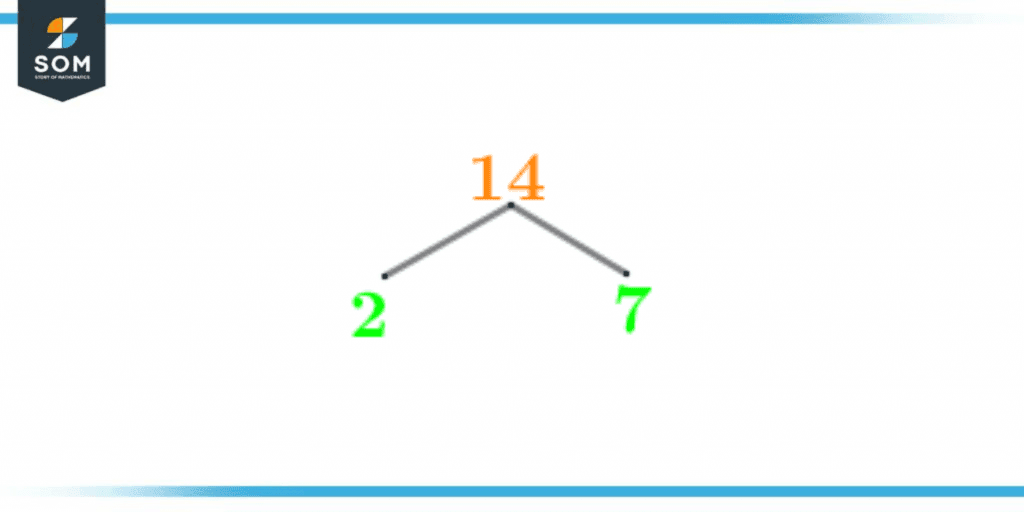
Figure 3 – Factor Tree of 14
Factors of 14 in Pairs
The factors of a number can also exist in the form of pairs and hence form factor pairs. A factor pair consists of two numbers which when multiplied together, give the original number as the product.
The factor pairs of 14 are given below:
1 x 14 = 14
2 x 7 = 14
So, the factor pairs of 14 are:
Factor Pairs = (1, 14), (2, 7)
The factor pairs can be both positive as well as negative. Negative factor pairs are similar to positive ones but the condition for negative factor pairs to exist is that both the numbers existing within the pair need to have a negative sign.
When these negative numbers are multiplied together, they produce a positive product and hence are considered as factors.
The negative factor pairs of 14 are given below:
-1 x -14 = 14
-2 x -7 = 14
Negative factor pairs of 14 are given below:
Factor Pairs = (-1, -14), (-2, -7)
How To Calculate the Total Number of Factors
The total number of factors existing for a number can be easily determined through a simple method. This method comprises of the factorization of the number.
For determining the total number of factors for 14, firstly determine the factorization of 14.
The factorization of 14 is given below:
Factorization of 14 = 1 x 2 x 7
After noting down the factorization of 14, next up determine the exponents of these factors and add one to each exponent. One 1 is added to each exponent, multiply these exponents together.
The product of these exponents then produces a number which is actually the total number of factors for a number.
In the case of the number 14, the exponent of all the factors 1, 2, and 7 is 1. Adding 1 to these exponents and multiplying them together gives 8.
Hence, the total number of factors of 14 is 8, where 4 are positive factors and 4 are negative factors. The total factors of 14 are given below:
Total factors of 14 = 1, -1, 2, -2, 7, -7, 14, and -14
Factors of 14 Solved Examples
To further understand the concept of factors of 14, let’s take a look at some simple examples constituting the factors of 14.
Example 1
Determine the average of all the factors of 14.
Solution
To determine the average of all the factors of 14, let’s first list down these factors. The factors of 14 are given below:
Factors of 14: 1, 2, 7, and 14
For determining the average, let’s first determine the sum of these factors.
Sum of factors of 14 = 1 + 2 + 7 + 14
Sum of factors of 14 = 24
The formula for average is given below:
\[ Average = \frac{\text{Sum of factors of 14}}{\text{Total number of factors of 14}}\]
\[ Average = \frac{24}{4} \]
Average = 6
Hence, the total average of all the factors of 14 is 6.
Example 2
Determine the common factors between the numbers 14 and 20 and find out their product.
Solution
For determining the product of the common factors of 14 and 20, let’s first list down these factors. The factors of 14 are given below:
Factors of 14: 1, 2, 7, 14
Similarly, the factors of 20 are given below:
Factors of 20: 1, 2, 4, 5, 10, 20
The common factors between 14 and 20 are given below:
Common factors: 1, 2
Hence the product of the common factors between 14 and 20 is:
Product = 1 x 2
Product = 2
Example 3
Calculate the product of all the factors of 14 and determine if the resulting number is an odd number or an even number.
Solution
To determine the product of the factors of 14, let’s first list down all the factors of 14.
The factors of 14 are given below:
Factors of 14 = 1, 2, 7, 14
Calculating the product of these factors:
Product = 1 x 2 x 7 x 14
Product = 196
So, the product of all the factors of 14 is 196.
Now, let’s determine if 196 is an odd or an even number. For this purpose, we need to figure out if 196 is a multiple of 2. The division of 196 with two is shown below:
196 $\div$ 2 = 98
Since a whole number quotient is produced when 196 is divided by 2 so that indicates that 196 is a multiple of 2 and hence, 196 is an even number.
Images/mathematical drawings are created with GeoGebra.
