JUMP TO TOPIC
Factors of 140: Prime Factorization, Methods, Tree, and Examples
Factors of 140 are the numbers that evenly divide 140, leaving zero as the remainder. Factors can also be defined as whole numbers that produce the required result when multiplied with another whole number. Algebraic equations can also be factorized.

Figure 1 – All possible Factors of 140
There are two types of factors:
- Positive Factors
- Negative Factors
In mathematics, there are two ways to factorize a number of an algebraic equation. One is the multiplication method the other one is the division method.
The real-life examples always make a new concept easy to understand. Let’s discover how we use factorization in our daily life. Factorization is a handy skill. Some common examples are, dividing shares among stakeholders, arranging files in rows, distributing sweets among students, etc.
In this article, we will learn a new concept of factors, what are the factors of 140, methods to find them, factor tree, and examples.
What Are The Factors of 140?
Factors of 140 are 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140. These numbers divide 140 evenly. The remainder is zero in every case.
140 is a positive even composite number. A number having more than two factors is known as the composite number. There are twelve total factors of 140.
How To Calculate the Factors of 140?
You can calculate the factors of 140 using two methods: multiplication and division methods. We will discuss both ways in this article.
First, find the factors of 140, and make a number line starting from 1 and ending on 140. We have to find the factors in this range.
Division
Factors of 140 by division method:
Every number is divisible by one; hence one is a factor of every whole number.
\[ \frac{140}{1} = 140 \]
1 and -1 both are factors of 140.
140 is an even number, so that it will be divisible by 2.
\[ \frac{140}{2} = 70 \]
Number 140 is completely divisible by 2. Hence 2 and -2 are factors of 140.
Let’s divide 140 by 3:
\[ \frac{140}{3} = 46.66 \]
When we divide 140 by 3, the result is not a whole number. The condition of factors is not satisfied. As a result, 3 is not a factor of 140.
Divide 140 by 4:
\[ \frac{140}{4} = 35 \]
4 and -4 are factors of 140.
Divide 140 by 5:
\[ \frac{140}{5} = 28 \]
5 and -5 are the factors of 140.
Divide 140 by 6:
\[ \frac{140}{6} = 23.3 \]
When we divide 140 by 6, the condition of factors is not satisfied. The remainder is not zero. As a result, 6 is not a factor of 140.
Similarly, we will divide 140 by the numbers within the range of our number line.
\[ \frac{140}{7} = 20 \]
\[ \frac{140}{10} = 14 \]
\[ \frac{140}{14} = 10 \]
\[ \frac{140}{20} = 7 \]
\[ \frac{140}{28} = 5 \]
\[ \frac{140}{35} = 4 \]
\[ \frac{140}{70} = 2 \]
\[ \frac{140}{140} = 1 \]
From the above calculations, we will write the factors list for 140.
Factors listed by division method:
Positive factors of 140 are: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140.
Negative factors of 140 are: -1, -2, -4, -5, -7, -10, -14, -20, -28, -35, -70, -140.
Factors of 140 by multiplication method:
Keep in mind the number line we generated earlier. In the multiplication method, both multiplicand and multiplier will lie on the number line, and the product must equal 140.
Following are the sets that give 140 on multiplication.
1 x 140 = 140
2 x 70 = 140
4 x 35 = 140
5 x 28 = 140
7 x 20 = 140
10 x 14 = 140
By the above multiplication, we conclude the factors list of 140.
Factors listed by multiplication method:
Positive factors of 140 are: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140.
Negative factors of 140 are: -1, -2, -4, -5, -7, -10, -14, -20, -28, -35, -70, -140.
Factors listed by multiplication are the same as factors obtained by the division method. You can opt for any method while calculating the factors of any number.
Factors of 140 by Prime Factorization
The approach used to express the number 140 as the product of its prime factors is known as the Prime Factorization of a number.
Prime numbers are integers divisible by one and the number itself. This means they have only two factors. Prime factors are the prime numbers in the list of factors.
Prime factorization is a method in which we track down the prime factors of a number. When these prime factors are multiplied by each other, we obtain the original number. Only composite numbers can be expressed in the form of prime factorization.
Finding prime factorization of 140:
Firstly divide the number 140 by the smallest prime factor present in the factors list.
The smallest prime factor in the list of factors of 140 is 2.
\[ \frac{140}{2} = 70 \]
70 is the quotient. It is again divisible by 2.
\[ \frac{70}{2} = 35 \]
The quotient is 35, which is not an even number, so that it wouldn’t be divisible by 2.
Now go for the next prime factor, which is 5.
\[ \frac{35}{5} = 7 \]
Again 7 is not divisible by 5. Find the next prime factor of 140 to proceed with the division.
The next prime factor is 7
\[ \frac{7}{7} = 1 \]
The quotient is 1. Hence division terminates here.
The Prime Factorization of 140 is shown below in figure 1:
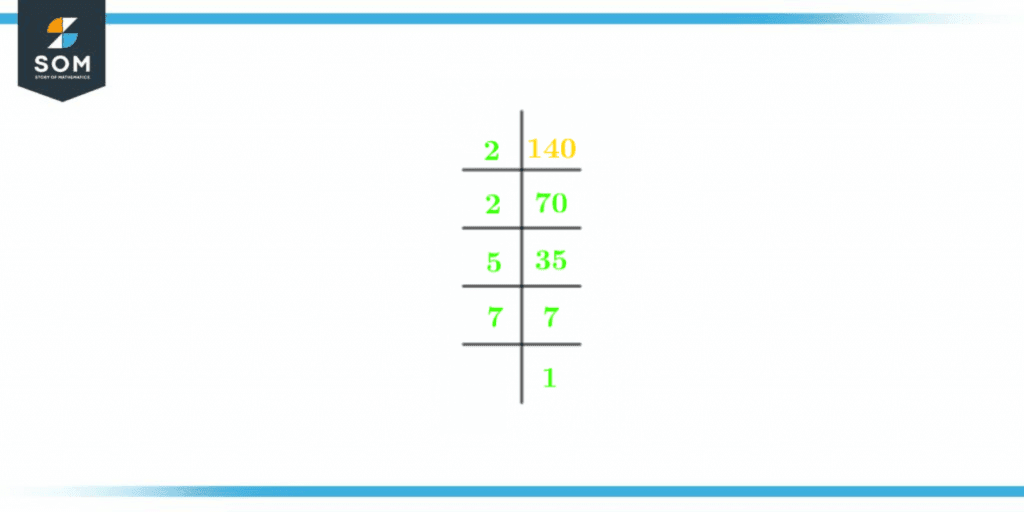
Figure 2 – Prime Factorization of 140
Factor Tree of 140
The factor tree is a graphical representation of factors of a number, specifically the prime factors. Its name says it all factor tree is like a tree with many branches and sub-branches. We’ll understand the phenomena behind the division of branches into sub-branches.
Now we will learn some tips and tricks to construct a factor tree:
Write the given number at the top, which is the starting point of the factor tree. Draw two branches out of it. Fill these branches with the factors of the number. One branch will have a prime factor, and the other will have a factor that is a composite number. Divide composite number. Keep on dividing until each branch ends up with the prime factors.
The factor tree of 140 is shown below in figure 2:
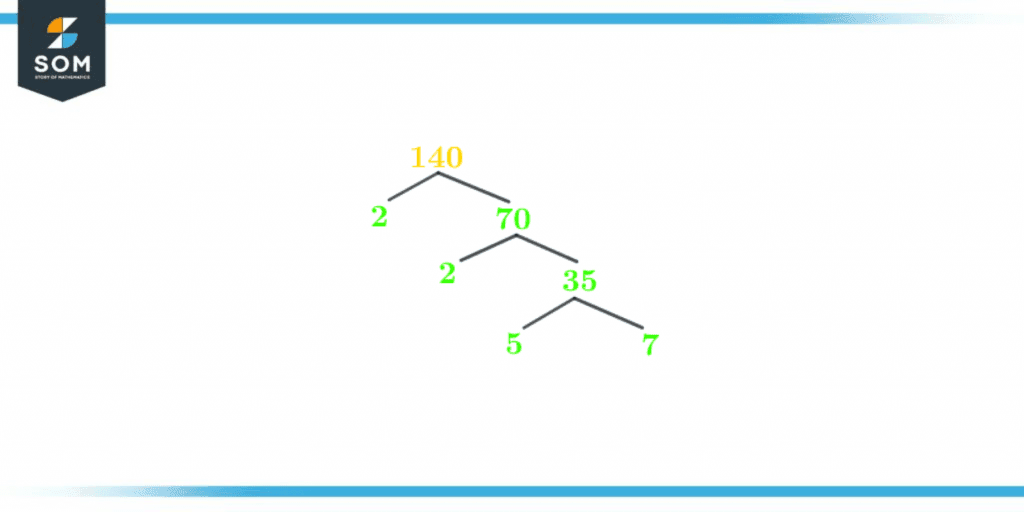
Figure 3 – Factor Tree of 140
The prime factorization of 140 can be written as:
2 x 2 x 5 x 7 =140
Factors of 140 in Pairs
Writing numbers in such pairs, when multiplied give a particular product that is equal to the original number. Such pairs are called factor pairs.
A simple multiplication method can be used to find factor pairs of a number.
Factor pairs can be positive and negative, but they can’t be in fractional form.
1 x 140 = 140
2 x 70 = 140
4 x 35 = 140
5 x 28 = 140
7 x 20 = 140
10 x 14 = 140
The positive factor pairs of 140 are given below:
(1, 140)
(2, 70)
(4, 35)
(5, 28)
(7, 20)
(10, 14)
The negative factors of 140 can be found as follows:
-1 x -140 = 140
-2 x -70 = 140
-4 x -35 = 140
-5 x -28 = 140
-7 x -20 = 140
-10 x -14 = 140
The law of signed multiplication is followed, saying that the product is always positive when a negative sign is multiplied by a negative sign.
The negative factor pairs of 140 are given as:
(-1, -140)
(-2, -70)
(-4, -35)
(-5, -28)
(-7, -20)
(-10, -14)
Positive and negative factor pairs are the same and differ by a negative sign.
Factors of 140 Solved Examples
Example 1
Find the sum of all factors of 140 and divide it by the sum of prime factors of 140.
Solution
Factors of 140: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140.
Finding the sum of all factors of 140
Sum 1: 1 + 2 + 4 + 5 + 7 + 10 + 14 + 20 + 28 + 35 + 70 + 140 = 336
Prime factors of 140: 2, 5, and 7.
Finding the sum of prime factors
Sum 2: 2 + 5 + 7 = 14
As per the question, divide Sum 1 by Sum 2
\[ \frac{336}{14} = 24 \]
24 is the answer.
Example 2
Find the common factors of 140 and 100. Also, find the product (P1) of all prime factors of 140 and divide it by the sum (S1)of all odd factors of 100.
Solution
Factors of 140 are: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140.
Factors of 100 are: 1, 2, 4, 5, 10, 20, 25, 50, 100.
Common factors are the numbers that are present in both lists of factors.
Common factors of 140 and 100: 1, 2, 4, 5, 10, and 20.
Prime factors of 140: 2, 5, and 7.
P1: 2 x 5 x 7 = 70
The odd factor of 100: 1, 5, and 25.
S1: 1 + 5 + 25 = 31
Now divide P1 by S1
\[ \frac{70}{31} = 2.25 \]
The result of division is 2.25.
All Images/mathematical drawings are created with GeoGebra.
