JUMP TO TOPIC
Factors of 144: Prime Factorization, Methods, Tree, and Examples
Factors of 144 are defined as all the natural numbers that divide the number 144 completely and leave no remainder behind.

Figure 1 – All possible Factors of 144
Alternatively, the factorization technique can also be defined as the two natural numbers which multiplied together in pairs to produce the number 144.
This article explains all the necessary information required to have a complete understanding of the factors of 144 and the different techniques to find these factors. The most commonly used methods are prime factorization and the division method.
Despite of techniques used to find factors, this write-up also explains the information regarding factor trees, and factors in pairs with solved examples.
What Are the Factors of 144?
Factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144.
The number 144, being an even composite number, has 15 factors as mentioned above. These said numbers are the perfect divisors of the number 144 which means that they do not leave any remainder behind upon dividing the number 144.
Factors of 144 are also called divisors of 144. The divisors of 144 can be classified into proper divisors and improper divisors.
How To Calculate the Factors of 144?
You can calculate the factors of 144 by using the divisibility test. For this purpose, 144 is divided by consecutive natural numbers to get a whole number quotient and zero remainders.
To find factors of 144, divide 144 by the smallest natural number which is 1.
\[ \dfrac{144 }{1} = 144 , r = 0 \]
As 1 has completely divided the number 144 and has left no remainder, so 1 is a factor of 144.
Now consider the next consecutive natural number in the count which is the smallest even prime number (2) to divide 144 into its factors.
\[\dfrac{144}{2} = 72 , r = 0 \]
It is clear that 2 divides the number 144 completely and produces a whole number in the quotient. Hence, it is also a factor of 144.
To find the rest of the factors of 144, divide 144 by the next consecutive number down in the list of natural numbers to see if it divides 144 completely or not.
\[ \dfrac{144}{3} = 48, r = 0 \]
\[\dfrac{144}{4} = 36, r = 0 \]
Now, divide 144 by the number 5;
\[\dfrac{144}{5} = 28.5, r ≠ 0 \]
As the resultant is not a whole number but a fraction in decimal. So, 5 is not a factor of 144.
Keep dividing 144 by the next numbers to find more factors.
\[\dfrac{144}{6} =24, r = 0\]
\[\dfrac{144}{8} = 18, r = 0\]
\[\dfrac{144}{9} = 16, r = 0\]
\[\dfrac{144}{12} = 12, r = 0\]
\[\dfrac{144}{144} = 1, r = 0\]
As all the above-mentioned numbers have completely divided the number 144 without leaving any remainder behind, so the factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144.
Important Properties
Following are some important and basic properties of the number 144 which must be kept in mind to help understand and find out the factors of 144.
- 144 is an even as well as a natural number.
- 144 is a composite number.
- 144 is a perfect square of the number 12.
- 144 is not a perfect number. In numbers theory, a perfect number is a positive integer that is equal to the sum of its proper factors.
Interesting Facts
For further understanding of the factors of 144, the following information must be recognized.
- The smallest factor of 144 is 1.
- Factors of a given number are always smaller than or equal to it. So, the largest factor of 144 is the number 144 itself.
- As 144 is an even number. Most of the factors of 144 are even numbers. Among all factors, only 1, 3, and 9 are odd numbers.
- It is interesting to note that the factors of 144 have only two prime factors (i.e., 2 and 3) and twelve composite factors (4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144). Whereas factor 1 does not fall in the category of either of these two types.
- The cross sum of the number 144 is 9 which is a multiple of 3.
- The sum of divisors of 144 is an odd composite number which is 403.
Factors of 144 by Prime Factorization
The prime factorization is the representation of a given number in form of the product of its prime factors. When the number 144 is represented as a product of all of its possible prime factors, it is called the prime factorization of the number 144.
Prime factors of a given number are most commonly found by using this method. The following steps are taken to find out the factors of 144 by this method.
At first, divide the given number (144) by the smallest prime number that divides it completely without leaving a remainder. The number produced as a result of this division is divided again by the smallest possible prime number.
This procedure keeps on going until the final quotient 1 is achieved which cannot be divided further.
Following are the steps to calculate factors of 144 by the prime factorization method.
The process is initiated by dividing the smallest available prime number (2) with the given number 144.
\[\dfrac{144}{2} = 72 \]
The resultant number (72) obtained from this division is divided again by the smallest possible prime number which, again, is 2.
\[\dfrac{72}{2} = 36 \]
Again, the quotient obtained is divisible by 2.
\[\dfrac{36}{2} = 18 \]
The resultant number is again divided by 2.
\[\dfrac{18}{2} = 9 \]
The resultant 9 is divisible by 3.
\[\dfrac{9}{3} = 3 \]
Finally divide 3 by itself as the last step.
\[\dfrac{3}{3} = 1 \]
Here, the final quotient received is 1 which cannot be divided any further and the procedure stops here. The prime factorization of 144 can be expressed as:
Prime Factorization = 2 × 2 × 2 × 2 × 3 × 3
Prime factorization of 144 can also be expressed as:
144 = 2$^4$ x 3$^2$
The prime factorization of 144 is represented by the following figure 1.
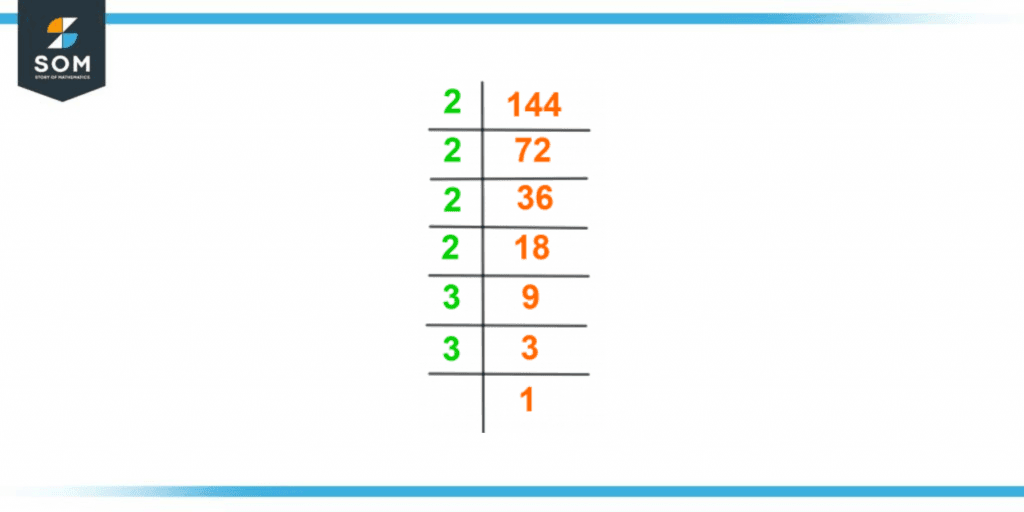
Figure 2 – Prime Factorization of 144
Factor Tree of 144
A factor tree is another method to find the factors of a given number. The procedure uses the basic rules of prime factorization for this purpose where the branching of the tree represents the division of the number under consideration.
The process is illustrated in the form of a tree undergoing the process of branching. The continuity of the branching depends on the presence of a composite number on either of the two branches resulting in the division.
The splitting of numbers stops at the point where a certain split produces prime numbers on both of its ends.
For the given number, considering the rules of division by the factor tree method, If we write 144 into multiples, it would be;
144 = 2 × 72
If we write 72 into multiples, it would be;
72 = 2 × 36
Repeat the procedure unless both the prime numbers appear in the split.
36 = 2 × 18
18 = 2 × 9
9 = 3 × 3
As the last division has produced both the prime numbers, the procedure stops here.
Representing a factor tree of 144 altogether in terms of its prime factors is given as:
2 × 2 × 2 × 2 × 3 × 3
The factors tree of 144 is represented in figure 2.
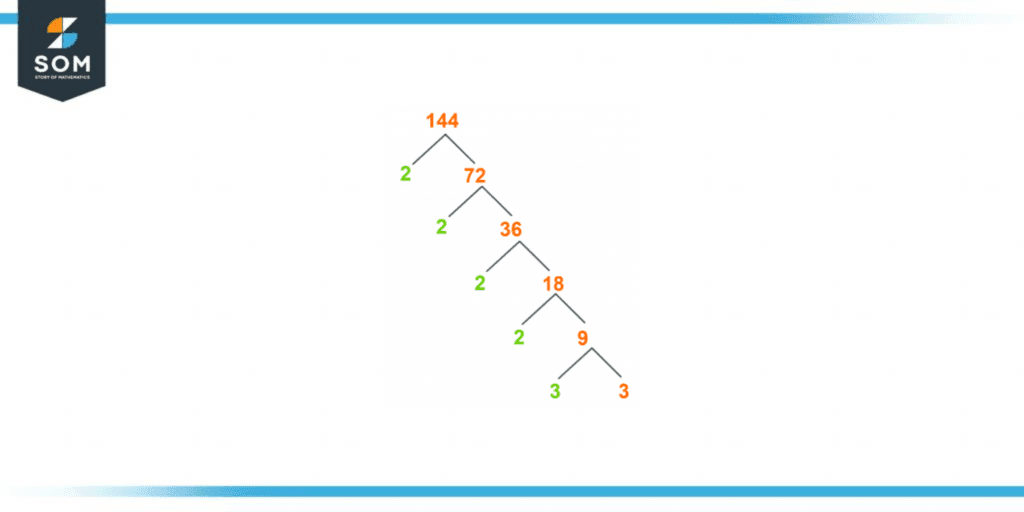
Figure 3 – Factor Tree of 144
Factors of 144 in Pairs
Factors of 144 in pairs are said to be the set of two natural numbers which multiply to produce the number 144.
In other words, it is the demonstration of the product of the factors of the number 144 in the form of pairs.
1 × 144 = 144
2 × 72 = 144
3 × 48 = 144
4 × 36 = 144
6 × 24 = 144
8 × 18 = 144
9 × 16 = 144
12 × 12 = 144
The number 144 has only 15 factors in total which can be represented in sets of pairs as follows:
(1, 144)
(2, 72)
(3, 48)
(4, 36)
(6, 24)
(8, 18)
(9, 16)
(12, 12)
The product of two negative numbers always produces a positive number. So, it is possible for the number 144 to have negative pair factors also.
(-2) × (-72) = 144
(-3) × (-48) = 144
(-4) × (-36) = 144
(-6) × (-24) = 144
(-8) × (-18) = 144
The negative pair factors of number 15 are as follows:
(-2, -72)
(-3, -48)
(-4, -36)
(-6, -24)
(-8, -18)
Important Tips:
- Only integers and whole numbers can be the factors of a given number.
- Decimals and fractions cannot be represented in the form of factors as factors are produced by the complete division of a given number.
- The number of pair factors remains the same for a given number in both its positive and negative forms.
Factors of 144 Solved Examples
Following are some solved examples:
Example 1
What is the prime factorization of 144?
Solution
The prime factorization of 144 can be shown as:
Prime Factorization = 2 × 2 × 2 × 2 × 3 × 3
Example 2
What is the sum of factors of 144?
Solution
As the factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144.
Sum of factors of 144 = 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 16 + 18 + 24 + 36 + 48 + 72 + 144
Sum of factors of 144 = 403
Images/mathematical drawings are created with GeoGebra
