JUMP TO TOPIC
Factors of 147: Prime Factorization, Methods, Tree, and Examples
The factors of 147 are the numbers that are divisible by 147. Factors can be defined as numbers that are wholly divisible without any remainder. Factors can be positive and negative with the difference of opposite signs.
Figure 1 – All possible Factors of 147
What Are the Factors of 147?
Factors 147 are 1, 3, 7, 21, 49, and 147, which shows that 147 is a composite number. All these numbers produce a zero remainder.The number 147 has six factors in total. These six factors can be separated into three separate factor pairs. The factors can be both positive as well as negative.How To Calculate the Factors of 147?
You can calculate the factors of 147 using different methods such as division, prime factorization, and factor tree diagrams. While the prime factorization and factor tree methods have been discussed in detail in the following sections, let us first look at the division method here. For this method, we divide 147 with multiple numbers and find the ones that leave no remainder.Finding factor 147 must be divided by a number, producing a non-decimal quotient. If there is a decimal present in the quotient, it means that the remainder is not zero. Hence that specific number is not a factor. The factors of 147 are calculated as follows through the division method. We start from 2, 3, 4, onwards until all the factors are known:Step 1: $\dfrac{147}{ 3} = 49 $
Upon division by 3, we get a whole number quotient; hence 3 is a factor.Step 2: $\dfrac{147}{ 7} = 21 $
Upon division with 7, we get a whole number quotient; hence 7 is a factor.Step 3: $\dfrac{147}{ 21} = 7 $
Dividing with 21 gives a whole number, so 21 is also a factor.Step 4: $\dfrac{147}{ 49} = 3$
49 is a factor because it divides 147 completely.Step 5: $\dfrac{147}{ 147 }= 1$
The number itself is always a factor.Step 6: $\dfrac{147}{ 1} = 147$
One is always a factor.Using the division method, we have:Factors of 147 = 1, 3, 7, 21, 49, and 147.Factors of 147 by Prime Factorization
Using prime factorization, we can represent any number through its prime factors. Multiplying these prime factors with each other will give back the original number. The prime factorization of 147 is shown below.Step 1: 147 $\div$ 3 = 49
In prime factorization, we start dividing the original number from the smallest prime number, which in our case is 3, the quotient we get is 49, which will act as the dividend for the next step.Step 2: 49 $\div$ 7 = 7
The following smallest prime number that divides 49 is seven, so we use that in this step. Quotient 7 will now act as the dividend for step 3.Step 3: 7 $\div$ 7 = 1
Seven, as we know, is a prime number and only divisible by itself, so we divide it by seven itself. The quotient is 1.Once we get a quotient equal to 1, no further division is possible; this is where our prime factorization ends.The above-performed procedure can be explained through a simple equation representing the prime factorization of 147:Prime Factorization of 147 = 3 x 7 x 7
Figure 1 attached below also explains the factorization of 147 in detail: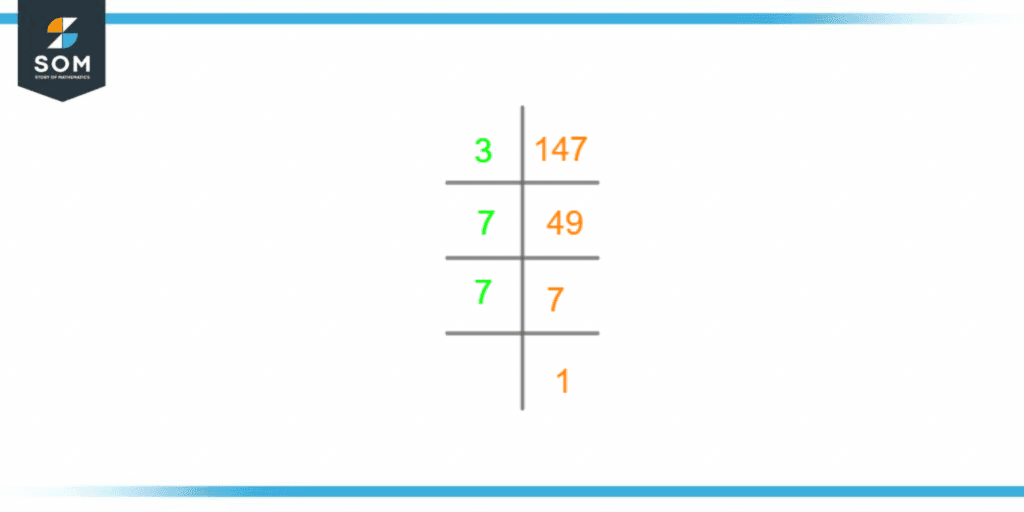
Figure 2 – Prime Factorization of 147
Factor Tree of 147
A factor tree is drawn to find out and show the prime factors of 147. It is just another method to find out the prime factors of 147 but what differentiates it from the prime factorization method is that it uses a visual diagram of a tree to represent the prime factors of 147. Built-in resemblance to the shape of a tree at the top of which we write the given number, once we start finding the factors, the tree also starts branching out into no more than two branches. The process stops once all branches end at prime numbers. Before drawing the tree, we should perform rough work and determine the prime factors of 147; dividing 147 by three gives us 49. On one branch, we write three, and on the other: 49. Now three can not be divided further, so we divide 49 into two branches, 7 and 7. As seven can not be divided further, our factor tree ends here.We have tried to explain the diagram making of a factor tree in this section, but for further clarity on the construction of a factor tree, it is recommended that you look at figure 2 given below: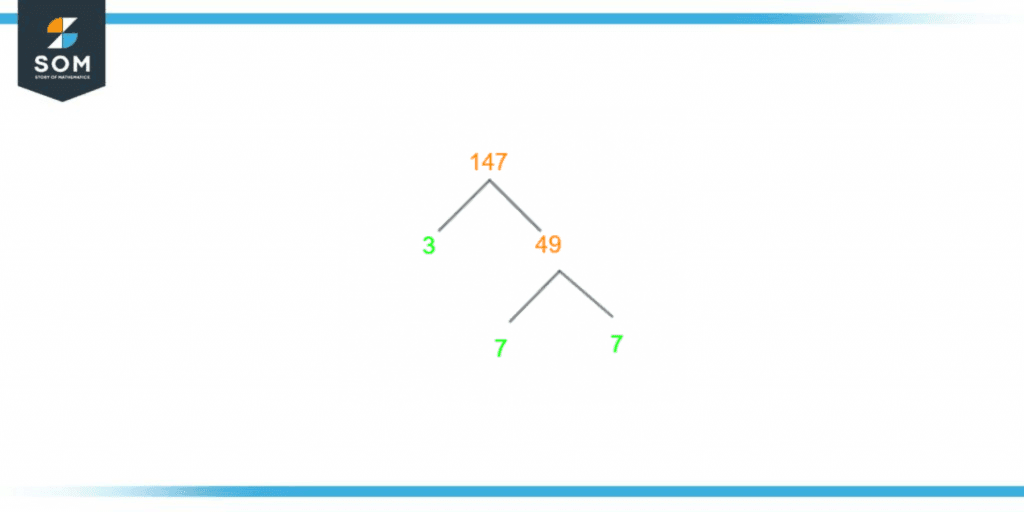
Figure 3 – Factor Tree of 147
Factors of 147 in Pairs
The factor pairs of 147 are a pair of factors that give 147 when multiplied by each other. Not every pair can give back 147 upon multiplication; it is a condition limited to only the right factor pair; hence, not all pairs are factor pairs.The fundamental factors of 147, according to the division method, are:Factors of 147 = 1, 3, 7, 21, 49, and 147.From these factors, it is interesting to note that no two factors will make a factor pair. Let us take 3 and 7, for example:3 x 7 = 21
As the multiplication of 7 and 3 does not give 147, we know that 3 and 7 do not make a factor pair.Similarly, let us take 21 and 49:21 x 49 = 1029
The product of 21 and 49 is also not equal to 147, so 21 and 49 are not a factor pair.21 x 7 = 147
As this product is equal to 147, so we know that 21 and 7 also make a factor pair.Working on this principle, we have the following positive factor pairs:Positive factor pairs of 147 = (1, 147), (3, 49), (7, 21)Just like positive factor pairs, we also have negative factor pairs; the only difference between them is the negative (-) sign with all integers. The negative factor pairs of 147 are:Negative factor pairs of 147 = (-1, -147), (-3, -49), (-7, -21)Factors of 147 Solved Examples
In the last section of this article, we will look at some examples of factorization of 147.Example 1
Explain the prime factorization of 147 step by step.Solution
The prime factorization of 147 is done through a repetitive process where 147 is divided by the smallest prime number. The resulting quotient takes the form of a dividend in the next step.We divide it with the smallest prime number divisor. The process is continued until we achieve the final answer equivalent to 1. The prime factorization of 147 is as follows:Step 1: 147 $\div$ 3 = 49
In prime factorization, we start dividing the original number from the smallest prime number, which in our case is 3, the quotient we get is 49, which will act as the dividend for the next step.Step 2: 49 $\div$ 7 = 7
The following smallest prime number that divides 49 is seven, so we use that in this step; the quotient seven will now act as the dividend for step 3.Step 3: 7 $\div$ 7 = 1
7, as we know, is a prime number and only divisible by itself, so we divide it by seven itself; the quotient is 1.The above step-by-step approach shows the prime factorization of 147, which also gives the prime factors of 147. Multiplying these prime factors will provide us with the original number in return. This equation can be represented as:Prime factorization of 147 = 3 x 7 x 7
