JUMP TO TOPIC
Factors of 15: Prime Factorization, Methods, and Examples
All the natural numbers that perfectly divide the number 15 leaving a whole number as the quotient and zero as the remainder are called the factors of 15.
Figure 1 – All possible Factors of 15
Important Properties
Following are some essential and fundamental properties of the number 15 which must be acknowledged to help find out the factors of 15.- 15 is an odd number.
- 15 is a composite number.
- 15 is not a perfect square.
What Are the Factors of 15?
The factors of 15 are 1, 3, 5, and 15. As 15 is an odd composite number, it has only 4 factors which are mentioned above. When 15 is divided by any of the mentioned numbers, it is divided wholly and does not leave any remainder. So, all of these numbers are said to be the perfect divisors of the number 15.How To Calculate the Factors of 15?
The basic division method can be used to find out the factors of 15. Consider the smallest natural number for this purpose to divide 15, if the remainder is 0, it will be a factor of 15.Dividing 15 by the smallest natural number is 1.\[\dfrac{15}{1} = 15 \]The number 15 has completely been divided by the 1 and has not left any remainder. So, 1 is a factor of 32.Now consider the smallest even prime number to divide 15 into its factors.\[\dfrac{15}{2} = 7.50 \]As the number 15 has not been divided evenly by the number 2. So, 2 is not a factor of 15To find out the remaining factors of 15, divided 15 by other natural numbers that completely divide 15 and leave no remainder.\[\dfrac{15}{3} = 5 \]\[\dfrac{15}{5} = 3 \]\[\dfrac{15}{15} = 1\]It can be noticed that the number 15 has completely been divided by these numbers and has left no remainder. Therefore, the only factors of 15 are 1, 3, 5, and 15. Following are some important which can help in the further understanding of the factors of 15.- The number 1 is the smallest factor of 15.
- Any given number cannot have a factor larger than itself. So, the largest factor of 15 is the number 15 itself.
- The number 15 only has the odd numbers as its factors.
- Number 15 has both Prime numbers (3 and 5) and a composite number (15) as its factors. Whereas, 1 is neither a prime nor a composite number.
- The number 15 has only one composite factor which is the 15 itself.
- The cross sum of the number 15 is 6. As 6 is divisible by 3. so, 15 is also divisible by 3.
- The Sum of divisors of 15 is 24.
Factors of 15 by Prime Factorization
When the number 15 is demonstrated as a product of all of its possible prime factors, it is called the prime factorization of the number 15. This method is most commonly used to calculate the factors of a given number.First, divide the number 15 by the smallest prime number which has the property to divide 15 completely without leaving any remainder.The resultant number from this division is divided again by the smallest prime number and the procedure keeps reoccurring until the final quotient is achieved as 1 which cannot be divided further.Following are the steps in sequence to calculate factors of 15 by the prime factorization method.The procedure is carried out by dividing the smallest available prime number which, in this case, is 3 with the given number 15.\[\dfrac{15}{3} = 5 \]As the quotient 5 is an odd prime number, it can only be divided further by 5.\[\dfrac{5}{5} = 1 \]The quotient 1 cannot be divided anymore and thus marks the procedure to stop.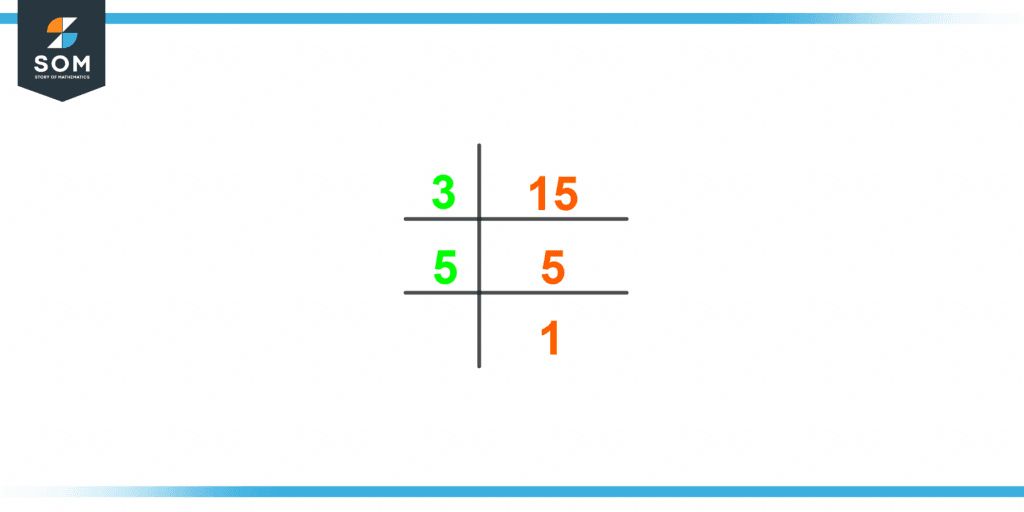
Figure 2 – Prime Factorization of 15
15 = 3 x 5
Factor Tree of 15
A factor tree is a method devised to easily find the factors of 15. It uses the rules of prime factorization presented in the form of a tree where the branching of the tree represents the division of the given number 15.When a branch splits, it produces either a prime or a composite number. As long as any one of the two branches has a composite number on it, the branching keeps going on until a split produces prime numbers on both of its branches which cannot be divided any further. Here, the branching stops.Considering the rules of division by factor tree method, If we write 15 into multiples, it would be:15 = 3 x 5
It is very important to note here that the number 15 has produced prime numbers on both of the branches in a single split. Thus, it cannot go on any further and its factor tree appears as follows: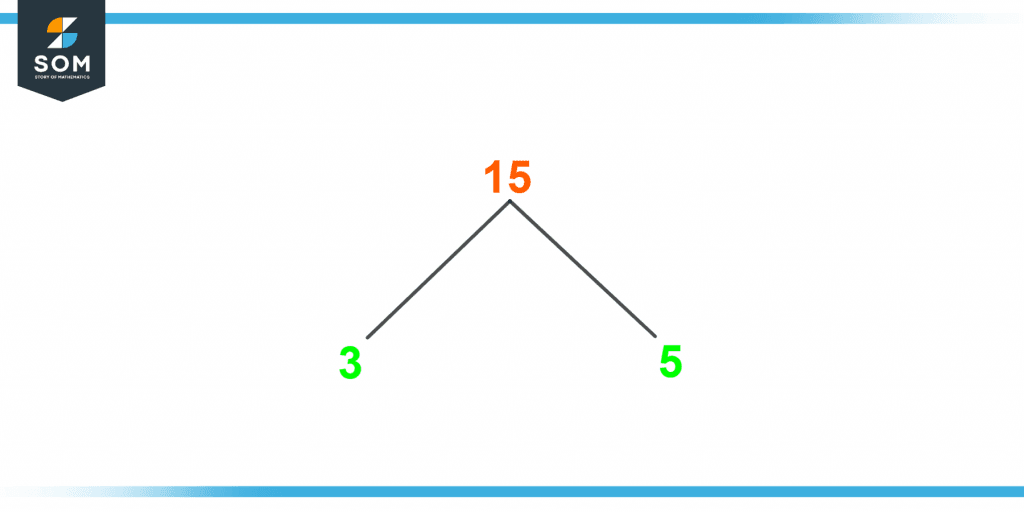
Figure 3 – Factor Tree of 15
Factors of 15 in Pairs
Factors of 15 in pairs are the set of two natural numbers that, when multiplied, produce the number 15.In other words, it is the product of the factors of the number 15 represented in the form of pairs.1 x 15 = 15
3 x 5 = 15
5 x 3 = 15
15 x 1 = 15
The number 15 has only 4 factors in total which can be written in sets of pairs as follows:(1, 15)
(3, 5)
The number 15 can have negative pair factors as well because the multiplication of two negative factors also produces a positive product.
(-1) x (-15) = 15
(-3) x (-5) = 15
The negative pair factors of number 15 are as follows:(-1, -15)
(-3, -5)
Important Tips
- Only integers and whole numbers can be the factors of a given number.
- Factors of a number cannot be in the form of decimals or fractions.
- A given number has the same pair of factors in both its positive and negative forms.
Factors of 15 Solved Examples
Following are some solved examples.
Example 1
Julia has been asked to pick a pair of factors with the following properties from a given set of pair factors of 15.- A pair factor with both factors as prime numbers.
(1, 15)
(3, 5)
Solution:
Consider the option given below:(3, 5)
Both of these factors cannot be divided completely by any other number and are divisible only by themselves and the number 1.So these numbers fulfill both of the conditions for factors of the pair of prime numbers.Hence, the correct option for Julia to choose is (3, 5).Example 2
John gets a pack of candies on Christmas. He decides to eat 3 candies daily. On the 5th day, the pack gets empty as John takes out 3 candies for the present day. Please help John to find out the total number of candies that the pack contained.Solution
The total number of candies that the pack contained can be found by the product of the total number of days John had eaten the candies and the number of candies he ate each day.Number of days = 5
Number of candies eaten per day = 3
Total number of candies the box contained = 5 x 3
Total number of candies the box contained = 15
Hence, the pack contained 15 candies.Example 3
Pick out the false statement about the factors of 15 from the following.- All the factors of 15 are odd numbers.
- Factors of 15 have only one composite number which is 15 itself.
- 15 can have a pair of one positive and one negative factor.
- Pair Factors of 15 can have one prime and one composite number.
Solution
When a positive number is multiplied by a negative number, the result is always a negative number. Since pair factors multiply to produce a given number, so the 3rd option is a false statement.Example 4
Stephen has been asked to pick a pair of factors of 15, where any of the two factors of the pair has all the following properties:- Odd number
- Composite number
(3, 5)
(-3, -5)
(1, 15)
