JUMP TO TOPIC
Factors of 16: Prime factorization, Methods, Tree, and Examples
A factor in mathematics is always a whole number that divides another number and gives off no remainder i.e. remainder will always be zero. Factors of 16 are the numbers that are completely divisible by the number itself.
Figure 1 – All possible Factors of 16
What Are the Factors of 16?
The number 16 has 5 factors that are 1, 2, 4, 8, and 16. In addition to this, every number has negative factors as well. These numbers give zero as a remainder. To find negative factors of a specific number you just have to reverse the sign. Thus, the negative factors of 16 are -1, -2, -4, -8, and -16.How to Calculate Factors of 16?
You can calculate the factors of 16 by two methods — multiplication and division. As 16 is a composite number, it means it is supposed to have more than 2 factors. You first have to start dividing the number with numbers between 1 to 8. Remember to only perform division of the number till 8 as a factor can not be a number more than half. Let’s take a few examples of the division of 16 with numbers:\[ \frac {16}{2} = 8 \]\[ \frac {16}{3} = 5.333.. \]The second division doesn’t have a factor of 16 because of 2 reasons:- It gives off a remainder.
- The answer to the division is not a whole number/ integer.
2 x 2 x 2 x 2 = 16
Factors of 16 by Prime Factorization
Expressing a number as a product of its prime factors is called prime factorization. It is a method in which we multiply prime numbers to obtain the product of the number. So, while we do prime factorization, you have to keep breaking the quotient until the number 1 becomes your answer. For the number 16, 2 will be your first choice as a prime number as selecting the smallest possible prime number is required. 2 is a prime number as it can only be divided by 1 or the number itself. Thus the division will look like this:\[ \frac{16}{2} = 8 \]The same process will be continued till 1 becomes our answer. \[ \frac{8}{2} = 4 \]\[ \frac{4}{2} = 2 \]\[ \frac{2}{2} = 1 \]Thus, it is confirmed that 2 is a prime factor of 16. The prime factorization of 16 can be mathematically written as:\[ 2^{4} = 16 \] The prime factorization is shown in the diagram below as well.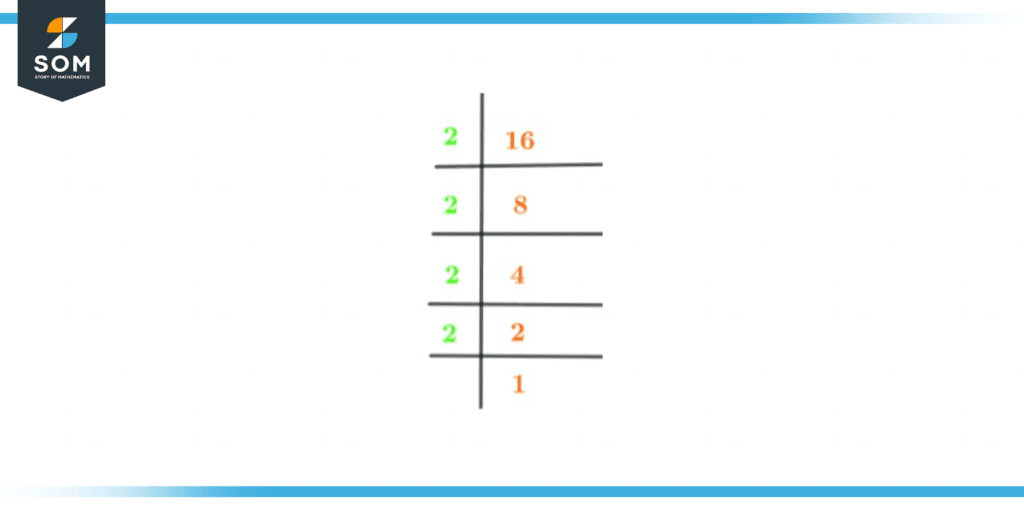
Figure 2 – Prime Factorization of 16
Factor Tree of 16
Just like we can represent the prime factors of a number through the diagram above, a factor tree is another way to represent the factors of a specific number through its branches. Once the factors can’t be factorized anymore, the branches are made no further. Prime factorization can be done by making a factor tree for a number. According to prime factorization, 2 is the only prime factor of the number 16. So, when simplified, 2 will be the last number on both branches of the factor tree. The factor tree of the number 16 can be seen below: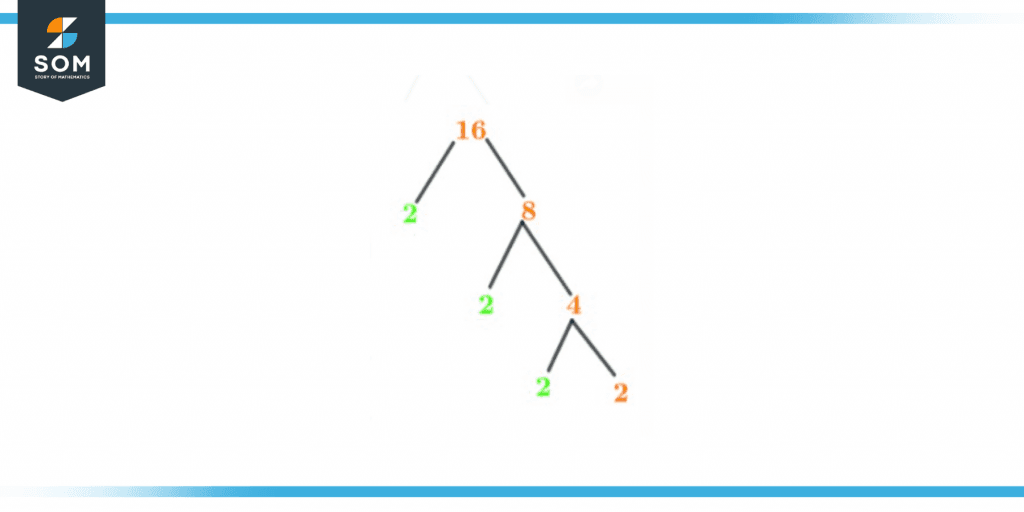
Figure 3 – Factor Tree of 16
Factors of 16 in Pairs
A factor pair is made when a number is divided by 16 and the remainder is zero and the answer is in whole numbers. In such a case, the quotient and divisor both are considered factors of the specific number and are called a Factor pair. The number 16 is called the product and the two numbers we get are factors of the number. To find factor pairs step number one is to find all the factors of 16. You can find them by any one of the methods mentioned at the start of this article.Once you have all the factors, start multiplying them with each other and the ones that answer 16 will be considered as a factor pair of the number 16. The factor pairs of 16 are (1, 16), (2, 8), and (4, 4).The negative factor pairs can also be written as they are nothing but the same factors with negative signs. The negative factor pairs of 16 are (-1, -16), (-2, -8), and (-4, -4).Factors of 16 Solved Examples
To further strengthen our concept of the factors of 16, let’s consider some examples given below.Example 1
What are the common factors of 12 and 16?Solution
To find the common factors of two numbers you first have to list all the factors of both the numbers and then start circling out the ones in common. The factors of 16 are:Factors: 1, 2, 4, 8, 16Whereas the factors of 12 are:Factors: 1, 2, 3, 4, 6, 12Thus, the common factors of the numbers 12 and 16 are:Common Factors: 1, 2, 4Example 2
What is the sum of factors of 16?Solution
A fact to remember when such a question comes up is that the keyword for addition is ‘sum’ and when you are required to subtract the keyword ‘difference’ will be given in the question. As of now we already know that the factors of 16 are 1, 2, 4, 8, and 16.Thus, we are simply required to add up all these factors together to get the answer.Hence, the sum of factors of 16 is:Sum of factors= 1 + 2 + 4 + 8 + 16
Sum =31
