JUMP TO TOPIC
Factors of 160: Prime Factorization, Methods, Tree, and Examples
Factors of 160 are numbers that may completely divide 160 or produce 160 when two values are multiplied together. An integer divides 160 by itself with a remainder of 0. Hence, it is considered to be a factor if it does so.
Figure 1 – All possible Factors of 160
What Are the Factors of 160?
Factors of 160 are as follows: 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80 and 160. As it is a composite number, 160 has more than two factors. In total, 160 has twelve factors.The numbers that divide 160 perfectly without giving a remainder are known as its factors. The factors can also be written in the form of factor pairs. For example, one of the factor pairs is (1, 160).How To Calculate the Factors of 160?
To Calculate the factors of 160, the following are the two main processes: Division and Multiplication.To find out if they have any factors, come up with a list of all the numbers that are less than or equal to the one you are looking for. Next, look over the list. For 160, the possible values will range from 1 to 80.
Then, by dividing each of them, one can obtain the answer. You can discover a number’s factor in two different ways: either by division or multiplication.
But even so, many methods exist for determining an integer’s factors. Once the remainder equals zero, you divide the original number by itself and consider the quotient and divisor factors of the provided number. As an example, let’s look at one of these situations.
32 is the result of 160 divided by 5. As a result, the divisor, as well as the solution, are considered factors. They are referred to collectively as factor pairs (5, 32).
1 x 160 = 160
2 x 80 = 160
4 x 40 = 160
5 x 32 = 160
8 x 20 = 160
10 x 16 = 160
Hence, the factors of 160 are mentioned above.Factors of 160 by Prime Factorization
Prime Factorization is a mathematical technique for expressing a number by a collection of factors multiplied together. It is a method for figuring out or showing a given integer as the sum of prime integers or in another manner.Described, it is a method for identifying or presenting a given integer as the sum of prime numbers. The prime factorization process is as follows:The smallest prime number evenly divides 160, leaving a 0 as the only remainder. After that, it is divided by the smallest or second smallest prime number again until the quotient is no longer divisible. Let’s divide 160 by the prime number 2. \[ \frac{160}{2} = 80 \]As the answer is a whole number, 2 and 80 are the factors of 160.We must now divide 80 by the following least prime number.\[ \frac{80}{2} = 40 \]Next, we divide 40 by 2, which gives us 20. Further division results in the following:\[ \frac{20}{2} = 10 \]\[ \frac{10}{2} = 5 \]Since 5 is a prime number, it is impossible to divide it further. Hence, 2 and 5 are the prime factors of 160. The notations used to indicate the prime factors of 160 are 2 x 2 x 2 x 2 x 2 x 5.The diagram below shows the prime factorization of 160: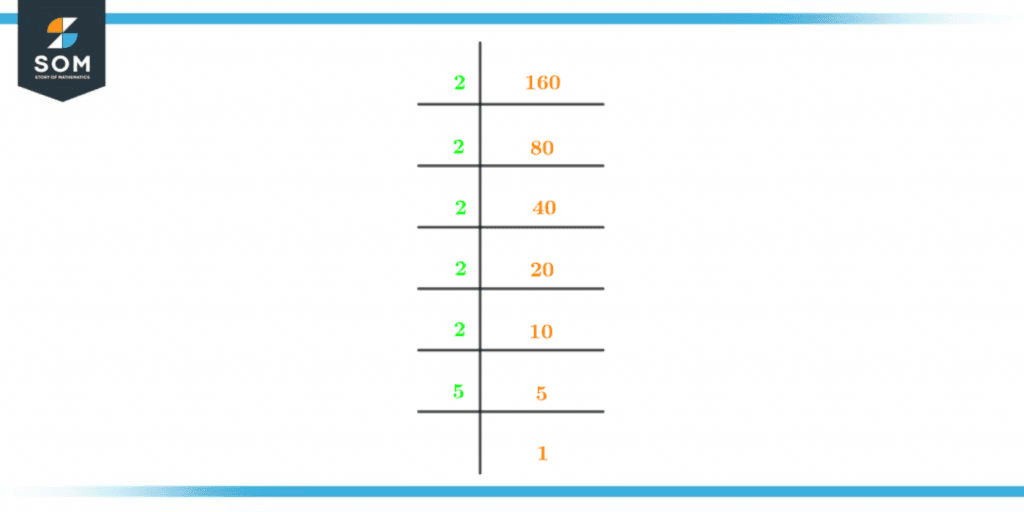
Figure 2 – Prime Factorization of 160
Factor Tree of 160
Even though a number’s factors can be represented in many different ways, one of the most common ways to graphically display a number’s prime factors is by using a Factor Tree.The actual number serves as the factor tree’s root, and branches extend to the prime number from this root. Thus, through prime factorization, 2 and 5 are regarded as the prime factors of 160.Below is the diagram which shows the factor tree of 160: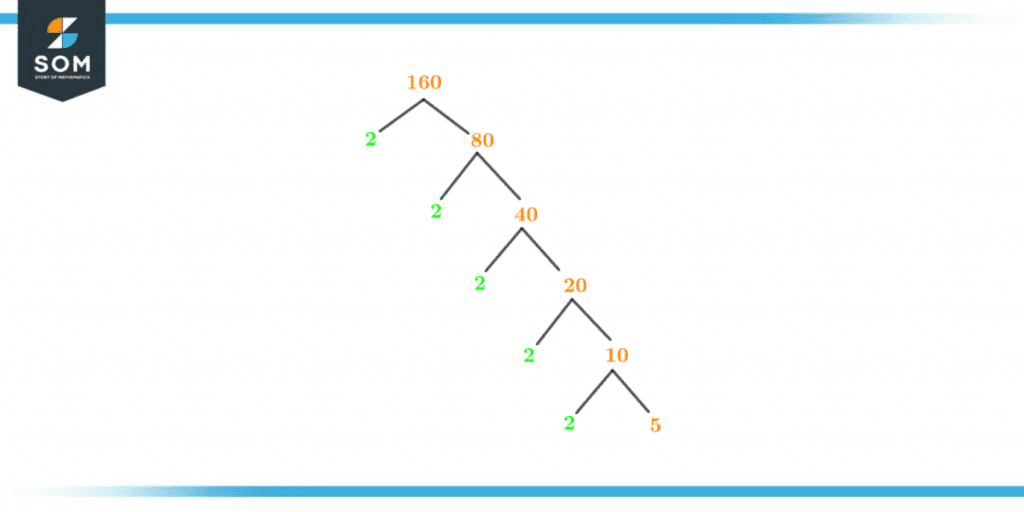
Figure 3 – Factor Tree of 160
- Together with the total of the cubes of the first three primes, the first 11 primes add up to 160.
- A basic short messaging service allows for 160 characters.
- The General Post Office in the United Kingdom managed the Dial-a-Disc (1966-1991) telephone number, which allowed callers to hear the most recent top 40 tunes. Its number was 160.
- 160 is an even, rational, and 3-digit number.
- All around the world, there are many highways numbered 160, specifically in Australia, Canada, Costa Rica, India, Japan, and the United States.
Factors of 160 in Pairs
Factor pairs are integers multiplied by one another in pairs to produce the number 160. Factor pairs are classified into two categories:- Positive factor pairs
- Negative factor pairs
Factors of 160 Solved Examples
Example 1
Ana needs help with a math question. The question is:Find the common factors between 120 and 160.Solution
The sixteen factors of 120 are the following:Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 and 120.
The twelve factors of 160 are the following:Factors of 160 = 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80 and 160.
The correct answer to the question is that 1, 2, 4, 5, 8, 10, 20, and 40 are the common factors between 120 and 160.Example 2
Add all the factors of 160.Solution
The composite number 160 has a total of twelve factors, which are:Factors of 160 = 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, and 160.
Sum = 1 + 4 + 2 + 5 + 10 + 8 + 16 + 32 + 20 + 40 + 160 + 80 = 378
Hence, the total of factors of 160 is 378.