JUMP TO TOPIC
Factors of 17: Prime Factorization, Methods, Tree, And Examples
The Factors of 17 are known as those numbers which produce zero as a remainder along with a whole number quotient when they act as the divisors for the number 17. In other words, these are the numbers which the number 17 is completely divisible.
Figure 1 – All possible Factors of 17
1 x 17 = 17
Such numbers form factor pairs. The number 17 is a simple prime number so the factors for this number are going to be the same as the factors for all the other prime numbers – the number 1 and the number itself. So in total, the number 17 has 2 factors.These factors of 17 can be determined through various mathematical phenomena such as the division method, the prime factorization method, and the factor tree. In this article, we will take a detailed overview of all these phenomena and will utilize them for determining the factors of 17. We will also dive into some solved examples of the factors of 17 to get a clear understanding of this concept.What Are the Factors of 17?
The factors of 17 are 1 and 17 and both of these factors are prime numbers. This is because the number 17 itself is a prime number so the factors it has are also prime numbers.When these factors act as the divisor for the number 17, the result is always a whole number quotient and a zero remainder.How To Calculate the Factors of 17?
You can calculate the factors of 17 through the most basic mathematics phenomenon which is the division method. The division method is entirely based on the division operation in which the number itself acts as the dividend and various numbers which can be possible factors act as the divisors.Before the application of the division method on the number 17, let’s first take a look at the basic conditions which act as the requirements for a number to be qualified as a factor.The first condition is that in order to be qualified as a factor, the number acting as the divisor must be able to produce zero as the remainder. The second condition is that apart from producing zero as the remainder, the number must also yield a whole number quotient.If these two requirements are met, then the number acting as the divisor is qualified to be a factor. Now, let’s dive into the application of the division method on the number 17. The number 17 is a prime number which indicates that the number must be divisible by itself. So let’s take a look at the division of 17 by 17 as shown below:\[ \frac{17}{17} = 1 \]As a whole number quotient 1 is produced, hence the number 17 acts as the factor. Another special aspect of the division method is that if a divisor qualifies to be a factor, then the whole number quotient it produces also acts as the factor. This statement can be understood by the following division:\[ \frac{17}{1} = 17 \]The number 1 was the whole number quotient obtained from the division of 17 by 17 and upon making 1 as the divisor, the number 17 is again divisible, which indicates that it also qualifies to be a factor.The factors of 17 obtained through the division method are given below:Factors of 17 = 1 and 17The factors of a number can be both positive as well as negative. The numerical value for the positive and the negative numbers is the same, the only difference is the sign that accompanies the number. So the negative factors of 17 are given below:Negative Factors of 17 = -1 and -17Factors of 17 by Prime Factorization
The prime factorization method is used for determining the prime factors of a number. The factors of any number can be both composites as well as prime numbers. These prime numbers which are the factors are known as the prime factors.In prime factorization, the entire division process is carried out with the help of prime numbers, where the quotient keeps taking the place of the dividend in the following steps as the division proceeds. This process is continued until 1 is obtained as the end result. In the case of the number 17, the number is a prime number which indicates that the factors this number constitutes are also prime numbers. Hence, all the factors of the prime number 17 are known as the prime factors.The prime factorization of the number 17 is shown below:Prime Factorization of 17 = 1 x 17
The prime factorization is also shown below in figure 1: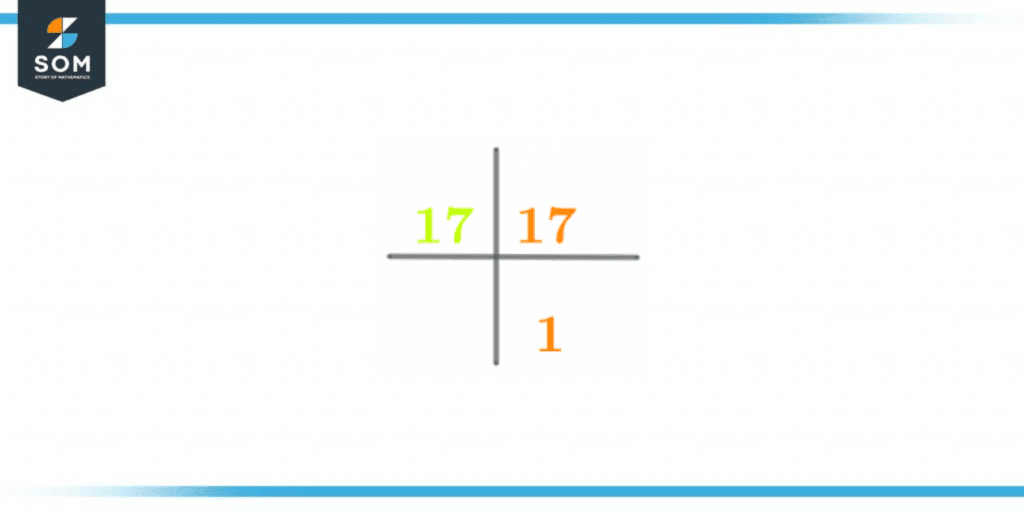
Figure 2 – Prime Factorization of 17
Factor Tree of 17
The factor tree is a tree-like structure that is used for determining the prime factors of a number. It can also be stated as the visual representation of the prime factorization method. In the factor tree, two branches extend out from the number – one holding the prime factor and the other holding the whole number quotient, which acts as the subject of division in the next step. At the last branches of the factor tree, only prime numbers are obtained which indicates the end of the factor tree. The factor tree for the number 17 is shown below in figure 2: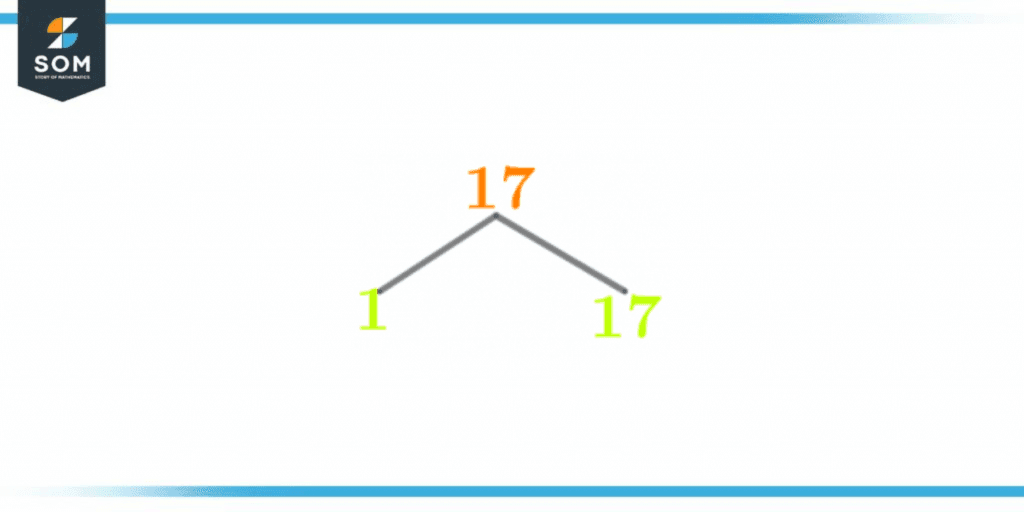
Figure 3 – Factor Tree of 17
Factors of 17 in Pairs
Lastly, the factors of any number can also exist in the form of simple pairs known as factor pairs. As the name suggests, the factor pair consists of a pair of numbers that not only act as the factors for the original number but also produce the original number as the result of their multiplication.As the number 17 is a prime number, so it only consists of 2 factors. These 2 factors join together to form a single factor pair. Hence, the factor pair for the number 17 is given below:1 x 17 = 17
Factor Pair of 17 = (1, 17)This factor pair can also compromise of negative factors. The only aspect that needs to be considered in a negative factor pair is that both the numbers within the factor pair must have a negative sign. This is so they could produce a positive product as a result of their multiplication.The negative factor pairs of the number 17 are given below:-1 x -17 = 17
Negative Factor Pair of 17 = (-1, -17)Some interesting facts for the number 17 are given below:- The number 17 is the only prime number that is the sum of the first four consecutive prime numbers: 2 + 3 + 5 + 7 = 17
- The sum of the individual digits of the number 17 is 8 which is an even number and a composite number: 1 + 7 = 8
- The number 17 is the seventh prime number in the series of the prime numbers
Factors of 17 Solved Examples
To delve more into the concept of the factors of 17, given below are a few solved examples involving the factors of 17 that can help you clear any additional ambiguity.Example 1
List down the factors of 17 and determine the difference between the sum of the factors of 17 and the sum of the digits in the number 17.Solution
To begin with the solution of this example, let’s first list down the factors of 17. The factors of 17 are given below:Factors of 17 = 1 and 17Now, let’s calculate their sum. Calculating the sum of the factors of 17:Sum of factors of 17 = 1 + 17
Sum of factors of 17 = 18
Now that we have determined the sum of the factors of 17, the next step is to determine the sum of the digits in the number 17.Sum of digits of the number 17 = 1 + 7
Sum of digits of the number 17 = 8
Now that we have determined both the sums, let’s calculate their difference to obtain the final solution.Difference = Sum of factors of 17 – Sum of digits of the number 17
Difference = 18 – 8
Difference = 10
Hence, the final solution obtained is the number 10.Example 2
Determine the average of the factors of 17.Solution
Firstly, let’s note down the factors of 17:Factors of 17 = 1 and 17Now, let’s calculate their average. The formula for average is given below:\[ Average = \frac{\text{Sum of factors of 17}}{\text{Total number of factors of 17}} \]\[ Average = \frac{1 + 17}{2} \]\[ Average = \frac{18}{2} \]Average = 9
Hence, the result obtained by calculating the average of all the factors of 17 is 9, which is a multiple of the number 3.All images/mathematical drawings are created with GeoGebra.