Factors of 176: Prime Factorization, Methods, Tree, and Examples

Factors can be explained as the numbers that are multiplied together to give a specific number. In simple words, it can also be explained as when a given number is divided by another number and it gives zero as the remainder, then it is called the factor of the given number. Every number has both positive factors and negative factors. We can exclude the negative factors as they are not commonly used.

Figure 1 – Factors obtained by Multiplication and Division Method

The number 176 has a total of 20 factors, out of which only 10 are positive.

What Are the Factors of 176?

The factors of 176 are 1, 2, 4, 8, 11, 16, 22, 44, 88, and 176 as they evenly divide the number 176 with zero remainders. 176 is an even number. Any whole number that divides 176 to give 0 as a remainder will be listed as a factor of 176. So, by dividing the number 176 and checking their divisibility we can form the factors list of 176. The list of Factors of 176 can be written in this form: Factors of 176 = 1, 2, 4, 8, 11, 16, 22, 44, 88, 176

How To Calculate the Factors of 176?

You can find the factors of 176 by multiplying the two numbers in pairs which produces 176 as the result.  The factors of 176 by pair multiplication are given as:

176 x 1 = 176 

1 x 176 = 176 

2 x 88 = 176 

88 x 2 = 176 

4 x 44 = 176

44 x 4 = 176 

8 x 22 = 176 

22 x 8 = 176 

11 x 16 = 176 

16 x 11 = 176 

Therefore from this method, it is concluded that 1, 2, 4, 8, 11, 16, 22, 44, 88, and 176 are the factors of 176. Another method that can be used to find the factors of 176 is the division method that helps to find the natural number that is exactly divisible by 176 without leaving the remainders. You should start by dividing the number 176 by the smallest natural number which is 1.

\[ \dfrac{176}{1} = 176\] 

This is the main method to find the factors of 176. Now, divide 176 by 2.

\[ \dfrac{176}{2} = 88  \]     

Again, the remainder is 0, which means that 2 is also the factor of 176. Now check the divisibility of 4.

\[ \dfrac{176}{4} = 44  \]  

Therefore, 4 is also the factor of 176. Repeat the same procedure for all the remaining numbers such that the remainder obtained is zero. \[ \dfrac{176}{8} = 22  \]   \[ \dfrac{176}{11} = 16  \]   \[ \dfrac{176}{16} = 11  \]   \[ \dfrac{176}{22} = 8  \]   \[ \dfrac{176}{44} = 4  \]   \[ \dfrac{176}{88} = 2 \]   \[ \dfrac{176}{176} = 1  \]   Therefore, all the above-mentioned numbers are the factors of number 176.

Factors of 176 by Prime Factorization

To find out if a number is evenly divisible by primes, you can try dividing it and seeing what the remainder is. If there’s no leftover then that would be an indication of prime numbers being the factors of the given number. This technique is called Prime Factorization. Prime factors of 176 are all those numbers that can only be divided by 1 and that number itself. Hence these factors, when multiplied answer 176. To find the prime factors you can follow the steps given below. Choose the smallest prime number factor i.e 2. Divide 176 by 2 

\[ \dfrac{176}{2} = 88  \] 

Now divide the answer with the number 2 

\[ \dfrac{88}{2} = 44  \]

We will keep on dividing the answer until we get a remainder in the answer

\[ \dfrac{44}{2} = 22  \]

Then:

\[ \dfrac{22}{2} = 11  \]

Since the answer is not further divisible by 2 without giving a remainder we will shift to the next prime number and will keep on repeating the steps until we get 1 in the answer.

11/11 = 1  

We can summarize all of the prime factors as:

2 x 2 x 2 x 2 x 11 = 176 

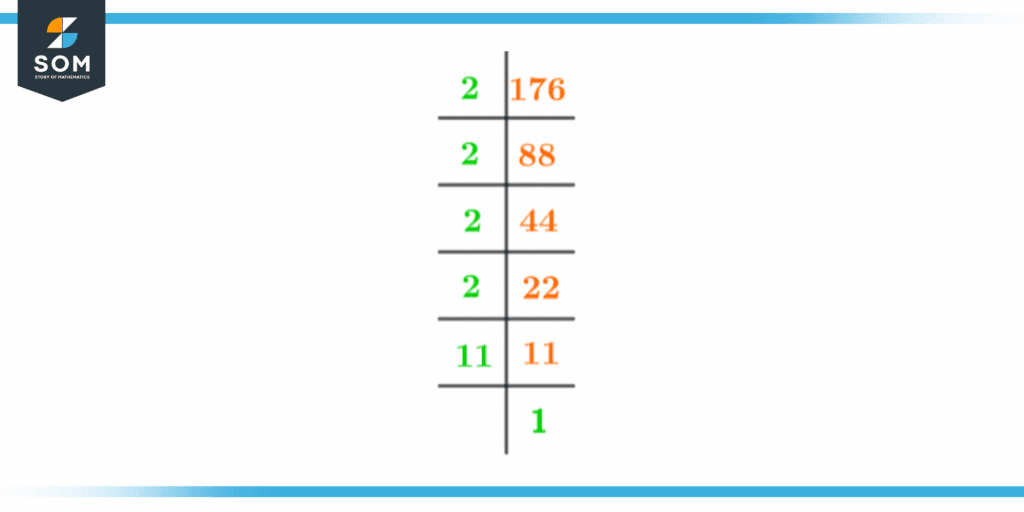
Figure 2 – Prime Factorization of 176

Factor Tree of 176

A factor tree is the pictorial description of the prime factorization of the given number. We can make a factor tree to understand the prime factorization even more. For that, we must clarify our prime factors concept. In total, we have 5 prime factors of 176 which are 2,2,2,2 and 11. Figure 1 given below is called a factor tree.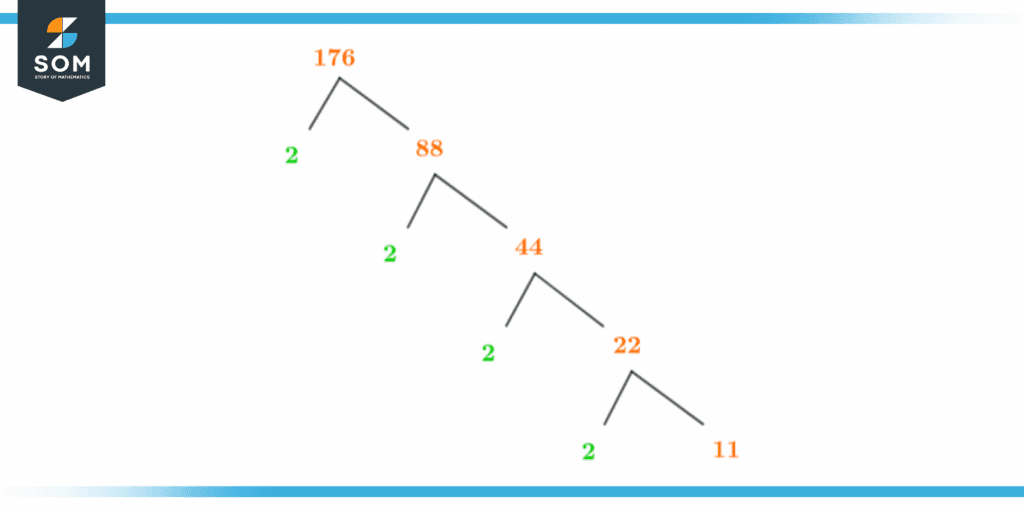

Figure 3 – Factor Tree of 176

Factors of 176 in Pairs

A factor pair is the product of two numbers that gives that certain number. For the number 176 we will find factor pairs by multiplying any two factors to give 176 as answer. For positive factors we can find pairs in this way:

1 x 176 = 176 

2 x 88 = 176 

4 x 44 = 176 

8 x 22 = 176 

11 x 16 = 176 

16 x 11 = 176 

22 x 8 = 176 

44 x 4 = 176 

88 x 2 = 176

176 x 1 = 176 

Note that each number when multiplied by the other gives 176 in the answer which tells that they are the positive factor of 176. Now for the negative factors of 176 we can also find the factor pairs. 

-1 x -176 = 176 

-2 x -88 = 176 

-4 x -44 = 176 

-8 x -22 = 176 

-11 x -16 = 176 

-16 x -11 = 176 

-22 x -8 = 176 

-44 x -4 = 176 

-88 x -2 = 176 

-176 x -1 = 176 

So, we can write the pairs in this way to summarize the factor pairs of 176:

Positive Factor pairs of 176 are (1, 176), (2, 88), (4, 44), (8, 22), and (11, 16). Negative Factor pairs of 176 are (-1, -176), (-2, -88), (-4, -44), (-8, -22), and (-11, -16).

Factors of 176 Solved Examples

Here are some solved examples involving the factors of number 176.

Example 1 – Product of Factors

Chrissy wants to know the product of all of the factors of 176 for her math homework. Help Chrissy find it.

Solution 1

The factors of 176 are:  1 ,2, 4, 8, 11, 16, 22, 44, 88, 176  Hence, the product of all these factors is as given below:

Product = 1 x 2 x 4 x 8 x 11 x 16 x 22 x 44 x 88 x 176

Example 2 – Enlisting Negative Factor Pairs

List all of the negative factor pairs of 176.

Solution 2

Negative factor pairs can be calculated by multiplying 2 negative factors by 176 and as two minus equals a plus so we will have 176 as an answer. We can check for every factor in this way:

 -1 × -176 = 176 

-2 × -88 = 176

-4 × -44 = 176 

 -8 × -22 = 176 

-11 × -16 = 176 

-16 × -11 = 176 

-22 × -8 = 176 

-44 × -4 = 176 

-88 × -2 = 176 

-176 × -1 = 176 

Negative Factor pairs of 176 are given as:

(-1, -176) 

(-2, -88)

(-4, -44)

(-8, -22)

(-11, -16) 

Example 3 – True/False

State whether the given statements are true or false. a) 22, 44, and 88 are factors of 176. b) 2 and 4 are prime factors of 176. c) -176 x -1 = -176 is correct equation.

Solution  3

a) True 22, 44, 88 are the factors as when 176 is divided by these numbers the remainder is zero   b) False 2 is a prime factor of 176 but 4 is not as the number 4 is itself divisible by 2. Prime factors of 176 are 2, 2, 2, 2, 11 c) False 2 minuses cancel out each other so the correct equation will be:

-176 x -1 = 176 

Images/mathematical drawings are created with GeoGebra. 

Factors Of 17 | All Factors | Factors Of 18