JUMP TO TOPIC
Factors of 18: Prime Factorization, Methods, Tree, and Examples
The Factors of 18 are the numbers that completely and evenly divide 18 and render zero as the remainder, along with a whole number quotient. These factors always product zero as the remainder when 18 is divided from them.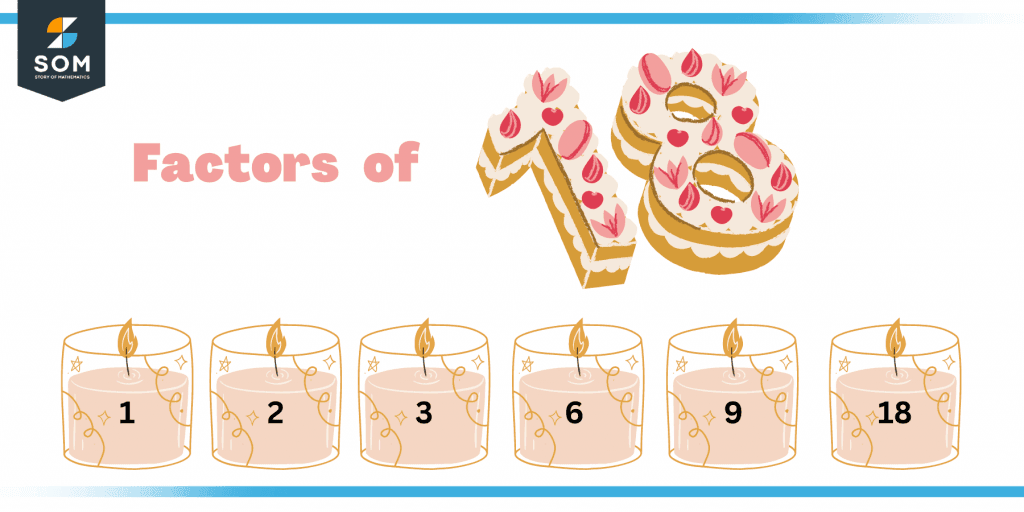
Figure 1 – All possible factors of 18
What are the Factors of 18?
The factors of 18 are 1, 2, 3, 6, 9, and 18. These numbers produce zero as the remainder and a whole number quotient when 18 is divided from them.In total, the number 18 has a total of 6 factors with 1 being the smallest factor and the number 18 itself being the largest factor.How to Calculate the Factors of 18?
You can calculate the factors of 18 by both the division method as well as the prime factorization method. Since 18 is an even number, so an easy way to determine the factors of 18 is to look for numbers between 1 and the half of 18, which is 9. Let’s take a look at the division method first. A unique aspect of the division method is that the number that produces zero as the remainder when 18 is divided from them also produces a whole number quotient.Both this number, the divisor, and the whole number quotient act as the factors of 18. A simple way to comprehend this statement is by looking at the following division:\[ \frac{18}{2} = 9 \]Since the division of 18 by 2 satisfies the condition for factors, hence 2 is a factor of 18. But an interesting thing to note is that it produces a whole number quotient, 9. So this quotient also acts as a factor.This can be proved by the following division:\[ \frac{18}{9} = 2 \]Hence, both the numbers 2 and 9 act as the factors of 18.Now, let’s consider the division from the number 3.\[ \frac{18}{3} = 6 \]This division indicates that both 3 and the number 6 act as the factors of 18. This statement is supported by the division of 18 with 6 as shown below:\[ \frac{18}{6} = 3 \]Hence, 3 and 6 are also factors of 18.Lastly, let’s consider the number 18 itself. The division is shown below:\[ \frac{18}{18} = 1\]Hence, both 18 and 1 also act as the factors of 18. So in total, 18 has a total of 6 factors and these are given below:Factors of 18 = 1, 2, 3, 6, 9, 18Factors of 18 by Prime Factorization
Prime Factorization is the method by which the prime factors of a number can be determined. Prime factorization is also an extension of the division method in which the division of a number through prime numbers is carried out until 1 is received at the end.For the prime factorization of the number 18, the division process is initiated by 2 as the divisor. This process is carried out until 1 is received at the end. This division of 18 by the prime number 2 is shown below:\[ \frac{18}{2} = 9 \]The product is 9 and the prime number used for the division of 9 is 3. So carrying out the division:\[ \frac{9}{3} = 3 \]\[ \frac{3}{3} =1 \]Since a 1 is obtained at the end through the division of prime numbers, hence this indicates that the prime factorization of 18 has been successfully completed. The prime factorization of 18 is also shown below: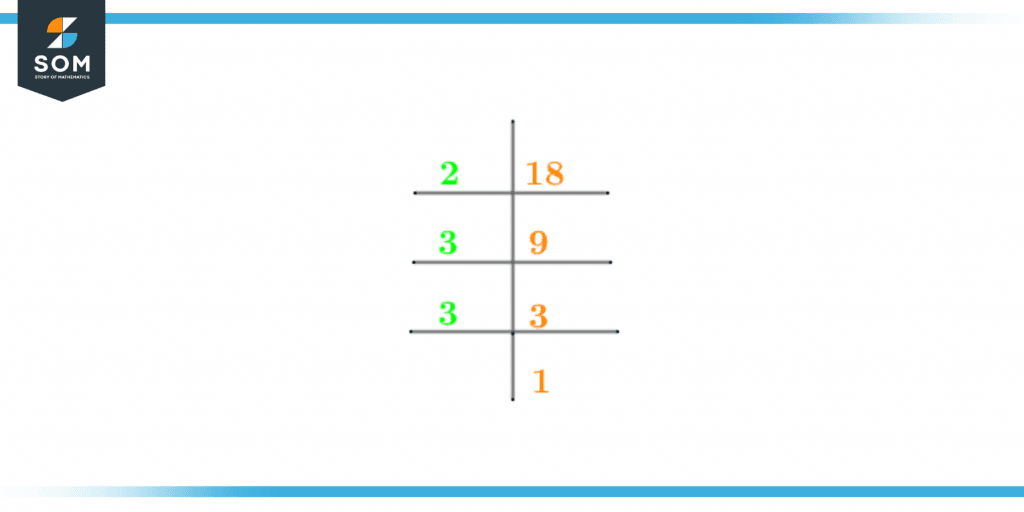
Figure 2 – Prime factorization of 18
Prime Factorization of 18 = 2 x 3 x 3
Prime Factorization of 18 = 2 x $3^{2}$
Factor Tree of 18
The factor tree is a visual representation of the division of the number through prime numbers. A factor tree is used to obtain prime factors for any given number, in this case, 18.A factor tree starts from the number itself and then extends its branches until prime factors are obtained. Since the objective is to obtain prime factors, so the factor tree must have prime numbers at its last branches. Similarly, the factor tree of 18 keeps on extending its branches until prime numbers are obtained at the end. The factor tree for the number 18 is shown below: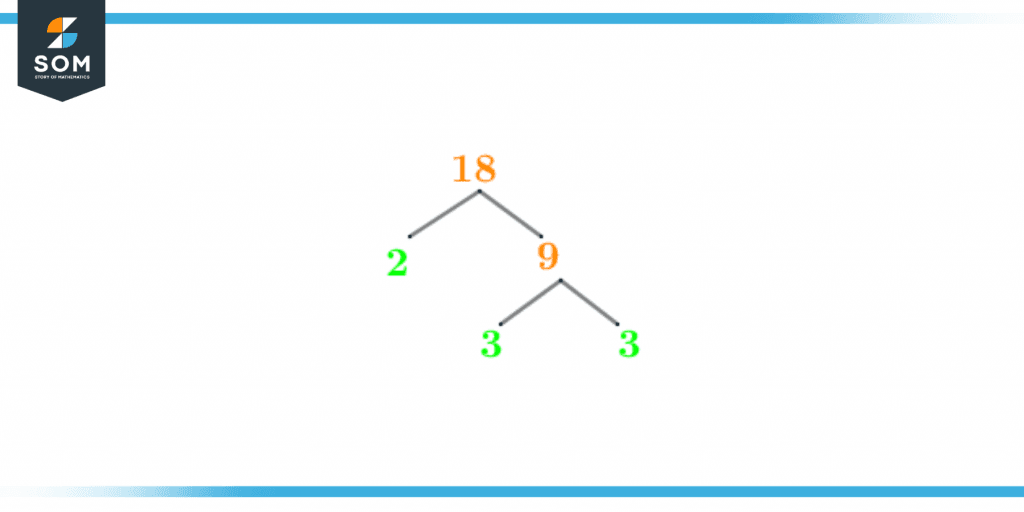
Figure 3 – Factor tree of 18
Factors of 18 in Pairs
Factor Pairs are the numbers that act as factors for a given number and also produce that said number when multiplied together.These numbers are written in the form of pairs. When the numbers in the pairs are multiplied, the original number is obtained, in this case, 18.Since 18 is an even number so it must be a multiple of 2. This is shown below:2 x 9 =18
Both 2 and 9 act as the factors of 18 and when multiplied together, they produce 18 as the product. Hence 2 and 9 constitute as a factor pair.Other similar factor pairs are given below:3 x 6 = 18
1 x 18 = 18
Hence, the possible factor pairs for 18 are given below:Factor Pairs of 18 = (2, 9),(3, 6), (1, 18) These factor pairs can be negative as well but the condition is that both the number within the pair need to be negative to produce a positive result.So the negative factor pairs of 18 are given below:Factor Pairs of 18 = (-2, -9),(-3, -6), (-1, -18) Some interesting facts for the number 18 are mentioned below:- 18 is a unique number which is a multiple of both 2 and 3.
- 18 is a special number whose half is 9 which is also the sum of its digits i.e, 1+18 = 9.
- 18 is a “semi-perfect” number, meaning that it is the sum of 3 of its factors, i.e, 3+6+9 = 18.
- 18 is the age in many countries where you legally become an adult.
Factors of 18 Solved Examples
To further enhance your understanding of the factors of 18, let’s take a look at some solved examples that will help to strengthen your concept of the factors of 18.Example 1
Calculate the average of the odd factors and the even factors of 18.Solution
For calculating the average of all the odd factors of 18, let’s first list down these factors.The factors of 18 are:Factors of 18 = 1, 2, 3, 6, 9, 18 Upon all these numbers, look for the odd factors. Odd numbers are those numbers that are not divisible by 2. So the following factors are the odd factors. Odd Factors of 18 = 1, 3, 9 Now, for calculating the average, consider the formula of average given below:\[ Average = \frac{\text{Sum of all the numbers}}{\text{Total numbers}} \]\[ Average = \frac{1+3+9}{3} \]\[ Average = \frac{13}{3} \]Average = 4.333
Hence, the average of all the odd factors of 18 is 4.333.Now, for the even factors, firstly list down the even factors. The even factors of 18 are given below:Even Factors of 18 = 2, 6, 18 The average for these factors is given as:\[ Average= {2+6+18}{3} \]\[ Average = {26}{3} \]Average = 8.667
Hence, the average of all the even factors of 18 is 8.667.Example 2
Determine the median of the factors of 18.Solution
For determining the median of the factors of 18, we will first list all the factors in ascending order.The factors in the ascending order are given below:Factors of 18 = 1, 2, 3, 6, 9, 18 Now, for calculating the median, you need to calculate the average of the middle two numbers. The middle two numbers in this case are 3 and 6 so we will calculate the average of 3 and 6.This average is given by:\[ Average = {3+6}{2} \]\[ Average = {9}{2} \]Average = 4.5
Hence, the median of the factors of 18 is 4.5Example 3
Find the range of all the factors of 18.Solution
Finding the range of the factors of 18 is pretty simple. Firstly, list down all the factors in an ascending order. The factors of 18 in an ascending order are given below:Factors of 18 = 1, 2, 3, 6, 9, 18 Now, for determining the range, consider the formula given below:Range = Highest value – Lowest Value
The highest value, in this case, is 18 and the lowest value, in this case, is 1.Substituting all the values in the formula of range:Range = 18 – 1
Range = 17
Hence, the range for the factors of 18 is 17. Images/mathematical drawings are created with GeoGebra.