JUMP TO TOPIC
Factors of 180: Prime Factorization, Methods, Tree, and Examples
Factors of 180 can be referred to as the numbers that may fully divide 180 or whose result is 180 when two numbers are multiplied together. Therefore, an integer is said to be a factor if it divides 180 by itself with a remainder of 0.
Figure 1 – All possible Factors of 180
What Are the Factors of 180?
The factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180. They are the number that gives no remainder when divided by 180. In another way, the factors of 180 are defined as the numbers multiplied in pairs to give the result 180. Many factors besides 1 and 180 make up 180 because it is an even composite number. In total, there are 18 factors out of 180.How To Calculate the Factors of 180?
To calculate the factors of 180, two methods that can be employed are division and multiplication. Let’s start by discussing how to use division to determine the factors.Division
Firstly, find all the figures that are less than equal to 180. Secondly, divide each number by 180. The divisions of 180 that have a remainder of 0 are known as its factors.The solution can then be found by halving each of them. Two is the factor of all numbers, an interesting fact about factors. Nevertheless, there are other approaches to finding integer factors. There is a method that is even more straightforward for finding factors of a number.
Let’s consider one of these scenarios as an example.
180 divided by two yields a value of 90. Thus, both the solution and the divisor are regarded as factors. They are referred to as factor pairs as a whole. (2, 90)
For a better understanding, let’s look at the example given below: We obtain 90 when we divide 180 by 2, the smallest factor of 180 other than 1. Therefore, the factors number 180 are 2 and 90. \[ \frac{180}{2} = 90 \]As the quotient is a whole integer and has no remainder, this demonstrates that the divisor and quotient (2 and 90) are both factors of 180. The following is a list of every factor of 180: \[ \frac{180}{1} = 180 \]\[ \frac{180}{2} = 90 \]\[ \frac{180}{3} = 60 \]\[ \frac{180}{4} = 45 \]\[ \frac{180}{5} = 36 \]\[ \frac{180}{6} = 30 \]\[ \frac{180}{9} = 20 \]\[ \frac{180}{10} = 18 \]\[ \frac{180}{12} = 15 \]Hence, stated above are all the factors of 180 by the division process.Multiplication
Let’s now understand the multiplication method to determine the factors of 180. In all possible scenarios, consider the number 180 will be the result of the multiplication. It is easier to find the factor pair as well using the multiplication method. Following are the possible multiplications:1 x 180 = 180
2 x 90 = 180
3 x 60 = 180
4 x 45 = 180
5 x 36 = 180
6 x 30 = 180
9 x 20 = 180
10 x 18 = 180
12 x 15 = 180
Thus, these are the factors of 180 i.e., 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180.Factors of 180 By Prime Factorization
The prime factorization technique involves the up-side-down division method to figure out the factors of the given number. Prime factorization is the way of determining the prime factors of 180.To put it more simply, it is a technique for determining or representing a given integer as the product of prime numbers. Following is the method of prime factorization: The smallest prime number divides 180 exactly, leaving a remainder of 0. After that, until the quotient becomes undividable, it is divided by the smallest or the second smallest prime number. Using the prime number 2, let’s divide 180. \[ \frac{180}{2} = 90 \]To complete this step, divide the next least prime integer by the quotient 90. \[ \frac{90}{2} = 45 \]Since 45 is an odd number, it can only be divided by three rather than two. 45/3 = 15 Moving on… \[ \frac{15}{3} = 5 \]We are unable to split the prime number five further. Thus, only 2, 3, and 5 are the prime factors of 180. To denote the prime factors of 180, the notations 2 x 2 x 3 x 3 x 5 are used.The diagram of the Prime factorization of 180 can be seen below: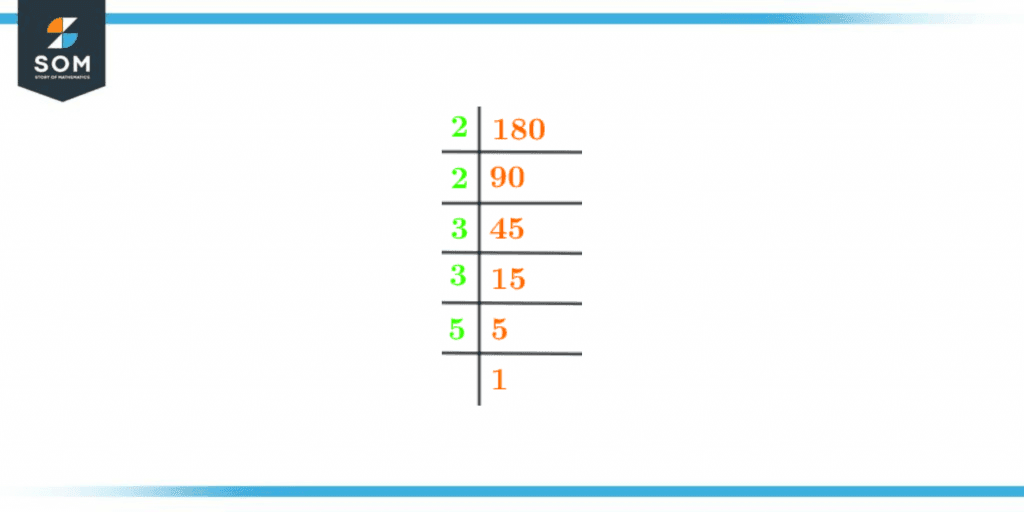
Figure 2 – Prime Factorization of 180
Factor Tree of 180
The factors of the number can be determined using various techniques, but the Factor tree is one of the several ways to display a number’s prime factors graphically. The factor tree’s root is the actual number, and the branches that emerge from it are up until you reach the prime number. Hence, it represents factors.As a result, 2, 3, and 5 are considered to be the prime factors of 180 by prime factorization. Therefore, the final integer representation in the factor tree should be 5. Factor Tree of 180 can be seen below: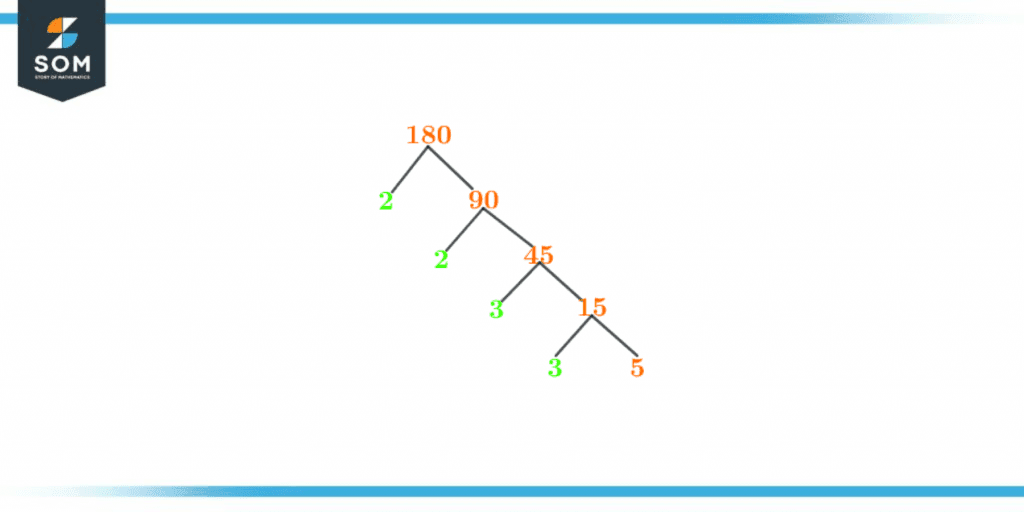
Figure 3 – Factor Tree of 180
- The sum of the three angles of a triangle is 180 degrees.
- 180 is a natural, rational and refactorable number.
- A U-turn is sometimes known as a 180 since half a circle has 180 degrees.
Factors of 180 in Pairs
A Factor pair is defined as the pair of two natural numbers that are the factors of 180; when multiplied, they yield the number as the outcome. The following is the list of the positive factor pairs of 180:1 × 180 = 180
(1, 180) is a pair factor of 180. Similar to that, let’s discover another pair.2 x 90 = 180
(2, 90) is a pair factor of 180.3 x 60 = 180
(3, 60) is a pair factor of 180.4 x 45 = 180
(4, 45) is a pair factor of 180.5 x 36 = 180
(5, 36) is a pair factor of 180.6 x 30 = 180
(6, 30) is a pair factor of 180.9 x 20 = 180
(9, 20) is a pair factor of 180.10 x 18 = 180
(10, 18) is a pair factor of 180.12 x 15 = 180
(12, 15) is a pair factor of 180. All that is required to identify the negative factor pair is to reverse the signs. The negative factor pairs are as follows:-1 x -180 = 180
(-1, -180) is a pair factor of 180.-2 x -90 = 180
(-2, -90) is a pair factor of 180.-3 x -60 = 180
(-3, -60) is a pair factor of 180.-4 x- 45 = 180
(-4, -45) is a pair factor of 180.-5 x -36 = 180
(-5, -36) is a pair factor of 180.-6 x -30 = 180
(-6, -30) is a pair factor of 180.-9 x -20 = 180
(-9, -20) is a pair factor of 180.-10 x -18 = 180
(-10, -18) is a pair factor of 180.-12 x -15 = 180
(-12, -15) is a pair factor of 180. Hence, these are the negative pair factors of 180.Factors of 180 Solved Examples
Example 1
List the factors 180 and 160. Also, find the common factors between them.Solution
The factors of 180 are given as follows:
Factor List of 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180
The factors of 160 are given as follows:
Factor List of 160: 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80 and 160
The common factors between 180 and 160 are 1, 2, 4, 5, 10, and 20.
Example 2
Find the sum of all the factors of 180.Solution
The factors of 180 are given as follows:1, 2, 3, 4, 5 follows, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
Sum = 1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 12 + 15 + 18 + 20 + 30 + 36 + 45 + 60 + 90 + 180 = 546
Thus, the sum is 546.
All images/mathematical drawings are made using GeoGebra.