JUMP TO TOPIC
Factors of 192: Prime Factorization, Methods, Tree, and Examples
Factors of any number are the complete divisors that produce zero remainders upon division with the given numbers. The factors of 92 are the group of natural numbers that are entirely divisible by 92 without any remainder. These can be calculated in multiple ways, which we will discuss in the following article.

Figure 1 – All possible Factors of 192
What Are the Factors of 192?
The factors of 192 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192. Since the number 192 is an even composite number, it consists of both prime and composite factors.
So the number 192 has 14 factors, and these 14 factors are grouped into 7-factor pairs.
How To Calculate the Factors of 192?
You can calculate the factors of 92 by using multiple methods, such as the division method and prime factorization. Before delving into other ways, we will first look at the division method to calculate the factors of 192.
Division
The division method depends on the division of 192 with any whole number; this whole number is a factor only if it divides 192 completely, which means that it does not produce any remainder. If there is a remainder upon division, the divisor is not a factor of 192
The entire method is shown below:
\[\frac{192}{ 2} = 96 \]
\[\frac{192}{3 }= 64 \]
\[\frac{192}{ 4} = 48 \]
\[ \frac{192}{ 6} = 32 \]
\[ \frac{192 }{ 8} = 24 \]
\[ \frac{192}{ 12} = 16 \]
\[ \frac{192 }{192} = 1 \]
The factors of 192 using this method are:
Factors of 192 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192.
Factors of 192 by Prime Factorization
The prime factorization method is similar to the division method, but we only divide the number with prime numbers. These provide a unique term for these factors known as prime factors.
Prime factors are the factors of a number but are prime in nature, meaning they are not divisible by any other number except one and the number itself. The existence of prime numbers makes this method unique because this number can be divided into prime factors.
Another property of prime factors is that when multiplied by each other, they must yield the original number. If they do not give back the original number, there is an error in your calculation, so this point must always be kept in mind.
In prime factorization, once divided by the prime number, the new quotient becomes the dividend for the next step; this is unique for this method, unlike the division method, where we are only looking for factors through a single-step approach. To improve your understanding of the prime factorization of 192, look below:
192 $\div$ 2 = 96
96 $\div$ 2 = 48
48 $\div$ 2 = 24
24 $\div$ 2 = 12
12 $\div$ 2 = 6
6 $\div$ 2 = 3
3 $\div$ 3 = 1
Once we achieve one as the answer, the factorization process is complete.
It can also be written down in the form of the equation below:
Prime Factorization of 192 = 2 x 2 x 2 x 2 x 2 x 2 x 3
Prime Factorization of 192 = $2^{6}$ x 3
The prime factorization of 192 in a figure is shown below:
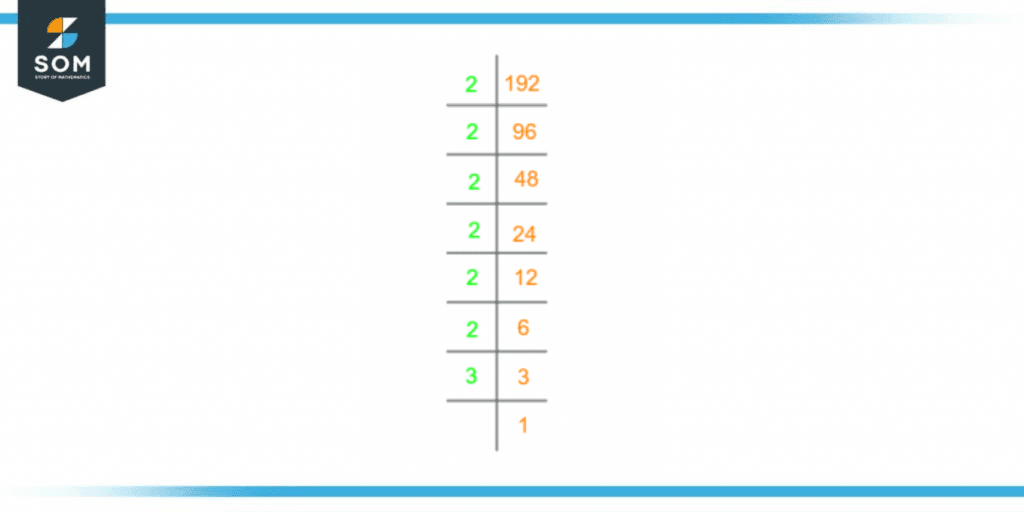
Figure 2 – Prime Factorization of 192
Factor Tree of 192
A factor tree is another method of performing prime factorization. The method depends on prime factorization but through a visual representation. Using a tree diagram, the given number sets at the head of the tree, which in our case is 192.
One thing to keep in mind is that in factor tree representation, we only use prime factors for a division like in prime factorization.
As we use the quotient as a dividend for the next step, similarly in the factor tree, we divide the quotient with its respective prime factor. The process continues until we reach all prime numbers at the roots of the tree.
To understand this technique better, it is imperative that we look at the diagram of a factor tree of 192 given below:
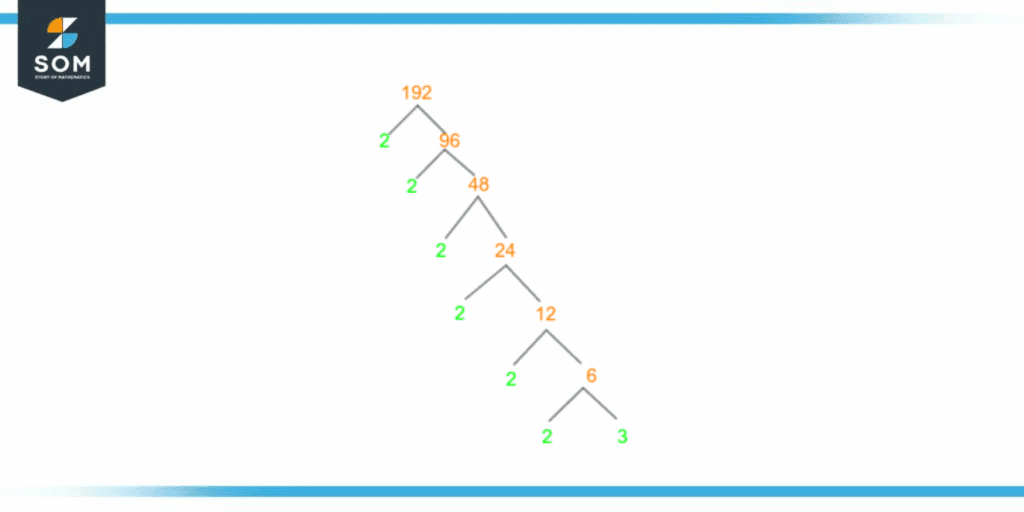
Figure 3 – Factor Tree of 192
Factors of 192 in Pairs
Factor pairs are a couple of factors that, when multiplied, give the original number from which the factors are calculated. In simpler terms, any two factors make a factor pair if their product gives back the real number.
Factor pairs are an entity common to all numbers. Even prime numbers have a factor pair where the number itself and the universal factor 1 make a pair. The number of factor pairs can range from two to the largest possible number for composite numbers.
We will now look at the factor pairs of 192; before that, let us revise the factors of 192:
Factors of 192 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192.
As 192 has 14 factors, we know it will make a total of 7-factor pairs from among its factors. The positive factor pairs of 192 are:
Positive factor pairs of 192 = (1, 192), (2, 96), (3, 64), (4, 48), (6, 32), (8, 24), (12, 16)
Without going into the details of negative integers, a simpler way of understanding negative factor pairs of 192 can just be written with a negative (-) sign as shown below:
Negative factor pairs of 192 = (-1, -192), (-2, -96), (-3, -64), (-4, -48), (-6, -32), (-8, -24), (-12, -16)
Factors of 192 Solved Examples
Now that we have thoroughly looked at theoretical mathematics let us apply our knowledge to a more practical side. We will be using examples in this section to demonstrate how each method can be applied to mathematical problems of factors of 192.
Example 1
Using the division method, find out the factors of 192.
Solution
This question asks us to use the division method to find out the factors. As we can recall from earlier, the division method is simple but performed to find such a number that, when divided by 192, will give us a zero remainder.
All such numbers that give a zero remainder when divided from 192 are called the factors of 192. Not only do they give a zero remainder but also a whole number quotient upon division. In this question, we will use this technique to find out the required factors. This method is shown in detail as follows:
The first step is to divide the given number 192 from 2:
\[ \frac{192 }{ 2} = 96\]
2 is a factor of 192 because it divides 192 completely; we move on to the next integer in the line.
\[ \frac{192}{ 3} = 64 \]
3 is also a factor of 192 as it gives 64 a whole number after division.
\[\frac{192}{ 4} = 48 \]
48 is a whole number, so we know that four must be a factor of 192.
\[ \frac{192 }{ 5}= 38.4 \]
After four, we tried division with 5, and this gave us a whole number meaning 38.4.
\[ \frac{192 }{ 6} = 32 \]
32 is a whole number, meaning that division by 6 gave a zero remainder; therefore, 6 and 32 are factors of 192.
\[ \frac{192}{ 8} = 24 \]
The fact that eight divided 192 completely into a whole number means that 8 is a factor of 192, and so is 24 because it is the quotient.
\[ \frac{192}{ 9} = 21.3 \]
21.3 is not a whole number because of the decimal place; therefore, 9 is not a factor of 192.
\[ \frac{192}{ 10} = 19.2 \]
19.2 is also not a whole number; therefore, 10 is not a factor of 192 as well.
\[ \frac{192}{ 12} = 16 \]
16 is a whole number, which means that 12 is also a factor of 192 and is the last factor we will also try for.
\[ \frac{192}{192 }= 1 \]
All numbers are divisible by themselves, so 192 is a factor along with 1.
The 10-step procedure mentioned above shows that the factors of 192 can be stated as 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192. It is because all quotients that result from the complete division are also factors. Hence the factors of 192 are:
Factor List of 192 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192.
Example 2
Find out the factors of 192 and 35 through the division method. Also, separate the even and odd factors of 192.
Solution
Example 1 has already shown us in detail the factors of 192, which are:
Factors of 192 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192.
Factors of 35 = 1, 5, 7, 35.
The even and odd factors of 192 are given below:
Even factors of 192 = 2, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, and 192.
Odd factors of 192 = 1 and 3
All images/mathematical drawings are created with GeoGebra.
