JUMP TO TOPIC
Factors of 24: Prime8 Factorization, Methods, Tree, and Examples
Factors of 24 correspond to a group of natural numbers that evenly divide 24 and leave zero as the remainder. Knowing the factors of all the numbers is important to better understand their real-world applications and relationships.
Figure 1 – All Factors of 24
What Are the Factors of 24?
Factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24. All of these are the factors of 24 as they divide 24 uniformly. The remainder is zero; hence, the necessary condition for the numbers to be the factor of 24 has been satisfied.24 is an even composite number, meaning it has more than two factors. Let’s find out how to calculate the factors of 24.How To Calculate the Factors of 24?
You can calculate the factors of 24 by determining the natural numbers in pairs that when multiplied together result in 24 as the product.Following are the numbers whose product is 24:1 x 24 = 24
2 x 12 = 24
3 x 8 = 24
4 x 6 = 24
So this shows that 1, 2, 3, 4, 6, 8, 12, and 24 are the factors of 24.Let’s introduce another method that can be used to factor the given number which is 24. The technique is to divide the number repeatedly to skim out the numbers that are divisible by 24. This method may seem difficult and tedious to perform for a large list of numbers but some simple tricks and divisibility rules of the number can help you to find factors quickly and easily. Here are some tips that can be helpful while finding the factors of 24.- 24 is an even number. Every even number is divisible by 2. So, 2 is the factor of 24.
- When 2 is divided by 24 the resulting quotient is 12. This means 12 is also the factor of 24 as the divisor and quotient both are regarded as the factors of the number.
- 24 is a multiple of 3, 6, and 8 as well. Therefore, all of them are the factors of 24.
- For all the numbers, two factors are common 1 and the number itself.
- The factors of 24 are not in the form of decimals or fractions.
Factors of 24 by Prime Factorization
Another technique used to determine the factors of the number is called Prime Factorization. Prime factorization is the way of multiplying the prime factors of a given number to create that particular number.Prime factorization demands reducing every composite factor of the given number into its prime factors so that the number is the product of its prime factors. To solve for the prime factors of 24 divide 24 by 2 first.Dividing 24 by 2 produces 12 as the quotient that can be further divided by 2 and results in 6. 6 is again the multiple of 2 so dividing it by 2 gives 3. 3 is an odd prime number so dividing it by 3 produces 1 and this is the end of prime factorization.The Prime Factorization of 24 is shown in figure 1 below: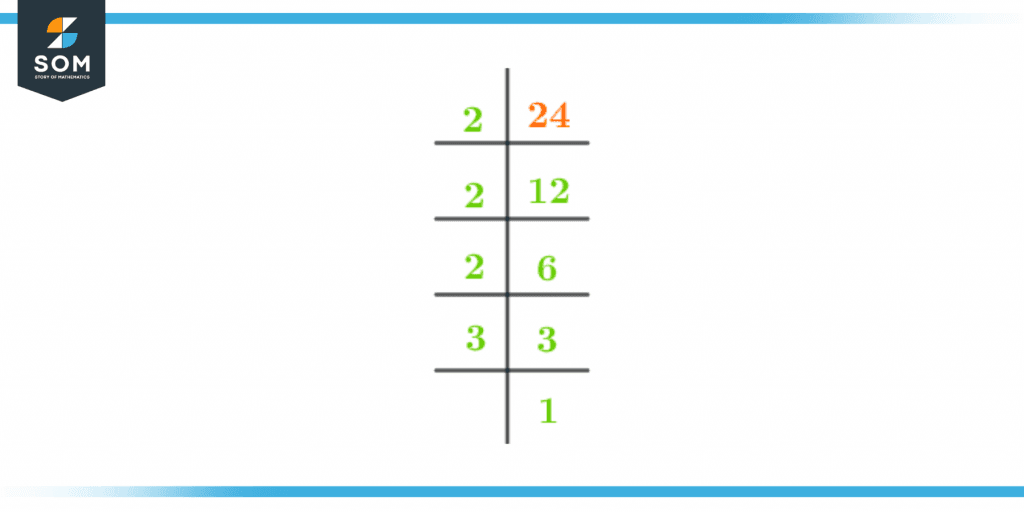
Figure 2 – Prime factorization of 24
LCM and HCF of 24
LCM and HCF are the resulting outcomes of prime factorization. LCM stands for Least Common Factor and HCF stands for Highest Common Factor.LCM can be found by finding the multiples of given numbers. The multiples of the numbers can be found using the Prime factorization technique. LCM is the smallest number that is common in both the list of factors of numbers determined.For instance, The LCM of 2 and 24 is 2 as 2 is the smallest common factor of both the numbers.HCF of the two numbers is the highest common factor or also called GCF stands for the greatest common factor. It is determined in the same way as LCM but instead of considering the smallest number common in factor lists of both the numbers, the highest common factor is considered.For instance, the HCF of 2 and 24 is 2.Factor Tree of 24
The factor tree is a visual representation of the prime factorization of 24. It shows how 24 splits into its prime factors.The factor tree of 24 is shown in figure 2 below: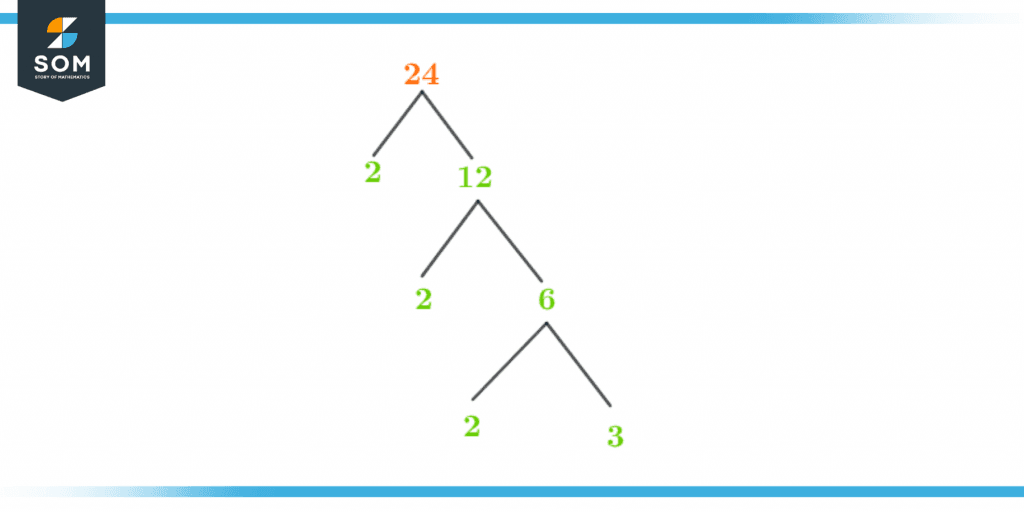
Figure 3 – Factor tree of 24
Prime Factorization of 24 = 2 x 2 x 2 x 3
Factors of 24 in Pairs
Writing the factors of 24 in pairs is the easiest way to group them in such a manner that their product results in 24.The factors can be found using the multiplication method:1 x 24 = 24
2 x 12 = 24
3 x 8 = 24
4 x 6 = 24
The factor pairs of 24 are given as:(1, 24)
(2, 12)
(3, 8)
(4, 6)
Therefore, 24 has 4 positive factor pairs. Similarly, we can also write negative factor pairs of 24 which are nothing but the same sets of numbers with negative signs as two negative signs multiply to give a positive sign. Hence yielding 24.The negative factors of 24 can be found as:-1 x -24 = 24
-2 x -12 = 24
-3 x -8 = 24
-4 x -6 = 24
The negative factor pairs of 24 are given as:(-1, -24)
(-2, -12)
(-3, -8)
(-4, -6)
Factors of 24 Solved Examples
Following are some solved examples related to the factors of 24.Example 1
What is the product of all the factors of 24 and 6?Solution
The factors of numbers 24 and 6 are given as:Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24Factors of 6 = 1, 2, 3, 6The product of both of the factors are given as:Product = 11943936Example 2
Find the HCF of 12 and 24.Solution
12 and 24 are factorized using the prime factorization technique.The factorization of 24 is given as:Factorization of 24 = $2^3$ x 3
The factorization of 12 is given as:Factorization of 12 = $2^2$ x 3
Common Factors are:C.F = 2 x 2 x 3
The HCF of 12 and 24 is given as:HCF = 12
Example 3
Find the LCM of 24 and 36.Solution
Let’s factorize both of them using prime factorization.The factorization of 24 is given as:Factorization of 24 = $2^3$ x 3
The factorization of 36 is given as:Factorization of 36 = 2 x 2 x 3 x 3
LCM is given as:LCM = 72
