JUMP TO TOPIC
Factors of 27: Prime Factorization, Methods, Tree, and Examples
Factors of 27 is a group of numbers consisting of integers that can evenly divide the number 27 without leaving any remainder behind. The pair of these numbers exist in such a way that when they are multiplied, the outcome is the original number of which they are a factor.

Figure 1 – All possible Factors of 27
Factors can be both positive and negative. Since the product of a negative and a positive integer is never a positive 27, the number 27 can only be obtained by multiplying two equally positive or negative numbers together, according to the principles of multiplication.
There are various techniques used to calculate the well-recognized factors of 27, some of the most commonly used approaches such as the division method, multiplication, and finally, the famous prime factorization technique going to be covered in the following article.
What Are the Factors of 27?
The factors of 27 are 1, 3, 9, and 27.
The fact that 27 is composite means that it contains more factors than simply the universal factor i.e. 1, and the number 27 itself. In other words, the factors of 27 are as follows,
Given that, the aforementioned factor list is responsible to divide the number 27 completely. The factors of any number can also be expressed by the laws of multiplication such that only the numbers that result in 27 as the product of their pairs are termed as the well-recognized factors of 27.
How To Calculate the Factors of 27?
You can calculate the factors of 27 by employing the division or multiplication methods.
By dividing the number 27 by a group of numbers (less than or equal to 27), the division method based on the rules of division produces a whole-number quotient and zero as the remainder.
As explained previously, 27 is a composite number. This nature of 27 allows the number to have a finite number of factors. In simple words, the total number of factors of 27 is 4.
By the laws of division, initially, we are going to divide the given number i.e. 27 with itself and the universal factor i.e. 1 such that,
\[ \dfrac {27}{1} = 27, r=0 \]
\[ \dfrac {27}{27} = 1, r=0 \]
As the remainder of the above division is zero and a quotient is a whole number by nature hence, the number 1 and 27 are considered as a factor of 27.
We will now proceed to divide 27 by a series of numbers as given below:
\[ \dfrac {27}{3} = 9, r=0 \]
\[ \dfrac {27}{9} = 3, r=0 \]
Where all the quotients are whole numbers and not fractions or decimal values. Also, the remainders of all the division processes are zero in nature.
Hence, 3, 9, and 27 are also the factors of 27.
As explained previously, laws of multiplication also play a vital role in computing the desired factors of any given number.
We are going to use the pair-multiplication methodology to calculate the factors of 27 such that, we will be multiplying a series of numbers that are less than or equal to the number 27, in pairs, and look for the product of multiplication. If the product of the multiplication of the number 27 itself, only then the multiplication will be considered fruitful.
The following is the required list of pair-multiplication for the factors of 27,
1 x 27 = 27, or
27 x 1 = 27
Similarly,
3 x 9 = 27, or
3 x 9 = 27
Hence,
Factors of 27 = 1, 3, 9, 27
The factors of any number can be both positive and negative integers such that, the negative factors of any number are the additive inverse of its positive factors.
Following is the list of the negative factors of 27.
Negative Factors of 27 = -1, -3, -9, -27
Similarly, the following is the list of the positive factors of 27.
Positive Factors of 27 = 1, 3, 9, 27
Fun Facts for factors of 27 are as follows,
- Since a number may be equally divided by itself, it is always a factor of itself. The same is true for 27. One of the factors of 27 is itself.
- The number 27 is a perfect cube of 3.
- The number 27 is odd but the sum of its factors is an even number.
(1+3+9+27) = 40
Factors of 27 by Prime Factorization
Prime factorization is yet another method used to determine the factors of any given number. Just like its name suggests, the technique works by calculating the factors of numbers that are all prime.
The upside-down division methodology is the technique used to calculate the prime factors of the number 27. The long division will be performed in such a way that the number 27 will initially be divided by its smallest expected prime factor, which is 3.
The division process will continue in such a manner that it will only come to an end when the number 1 appears as the end quotient, signifying that no further division is possible.
The prime factorization of 27 is given as follows:
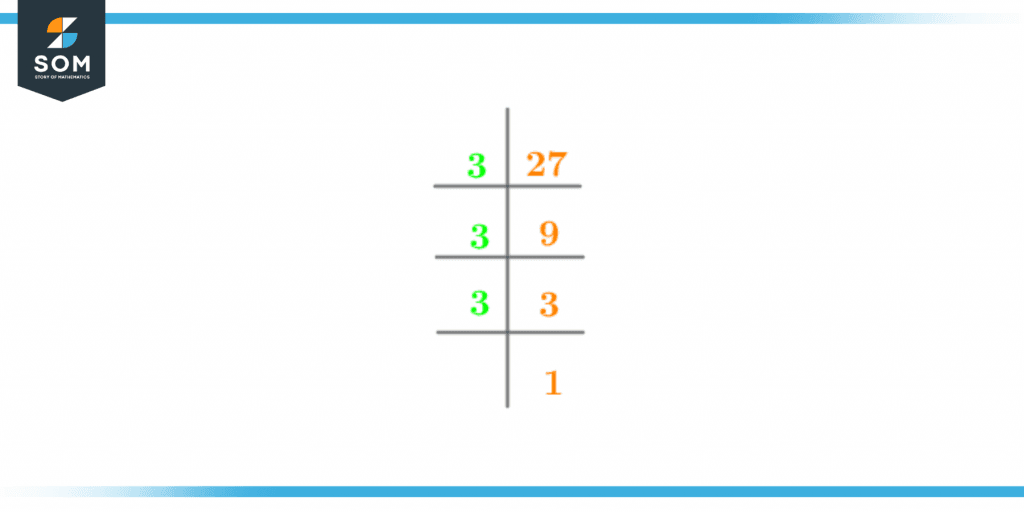
Figure 2 – Prime Factorization of 27
The prime factorization of 27 can also be expressed as the following expression,
3 x 3 x 3 = 27
Hence, there are 3 prime factors of 27.
Prime Factors of 27 = 3, 3, 3
Factor Tree of 27
A factor tree, as its name indicates, is a pictorial portrayal of factors of any number, where each factor is represented by a branch of the tree. In simple words, a factor tree is the graphical representation of the prime factors of a number.
Do you want to find the prime factors of 27, by using the factor tree?
Let’s calculate factors of 27 by splitting the number 27 into its factors that are further broken into their prime factors. Such that,
27 = 3 x 9
9 = 3 x 3
The following image shows the factor tree of the number 27,
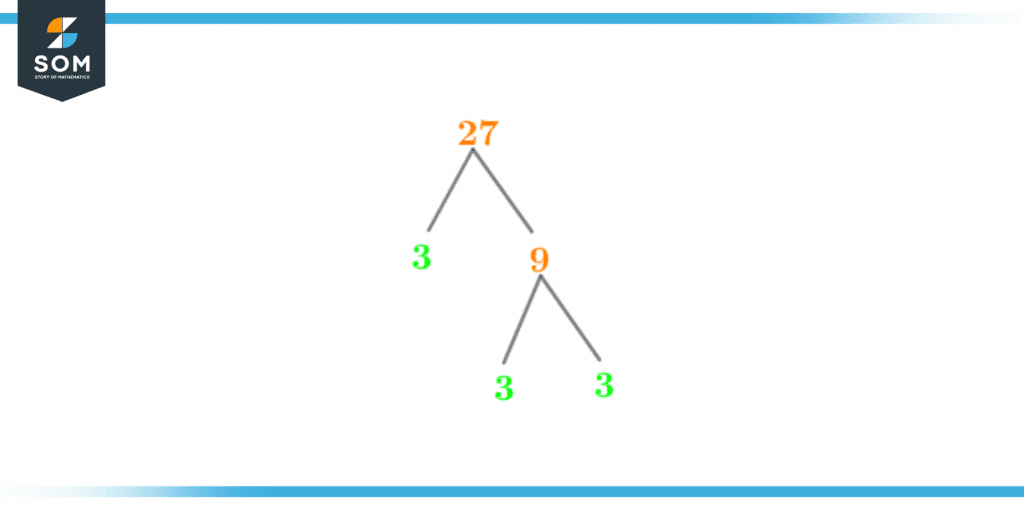
Figure 3 – Factor Tree of 27
Factors of 27 in Pairs
The sets of numbers that make up the pairs of factors are those that, when multiplied together, provide the same result as the product of which they are a factor.
When they produce the number 27 as the result of their multiplication, the factors of 27 are referred to as the pair factors. The number 27 fortunately has two pairs of factors.
The pair of factors of the number 27 are represented as:
1 x 27 = 27
Where, (1, 27) is a factor pair of 27.
Similarly, the next factors pair is given as:
3 x 9 = 27
Hence, (3, 9) is also a factor pair of 27.
As explained before, the factors of any number can be both positive and negative integers that when combined in pairs, result in producing the original number they are a factor of.
Hence, the pair of factors of 27 can also be written as:
-1 x -27 = 27
Where, (-1, -27) is a factor pair of 27.
Similarly:
-3 x -9 = 27
Hence, (-3, -9) is also a factor pair of 27.
In other words,
Positive Factor Pairs of 27 = (1, 27), (3, 9)
Negative Factor Pairs of 27 = (-1, -27), (-3, -9)
Factors of 27 Solved Examples
Let’s solve a few examples to test our understanding of the above article.
Example 1
Oscar wants to know which of the following statements are true. Can you help her out in finding the correct answers?
- There are a total of 5 factors of 27.
- The negative factor pairs of 27 are, (-1, -27) and (-3, -9).
- The number 27 is prime.
Solution
Given that:
- Answer = False
The following is the list of factors of 27,
Factors of 27 = 1, 3, 9, 27
According to the above-mentioned list, there are a total of 4 factors of 27.
- Answer = True
Negative Factor Pairs of 27 = (-1, -27), (-3, -9)
- Answer = False
The number 27 is not prime as it has factors more than just the universal factor and itself.
The following is the list of factors of 27,
Factors of 27 = 1, 3, 9, 27
Hence, the number 27 is composite.
Example 2
John bought 27 pots out of which he sold x number of pots in 3 days. Can you find the correct number of soled pots?
Solution
Given that:
\[ \dfrac {27}{x} = 3 \]
27 = 3 x x
Such that, remembering the factor pairs of 27.
Factor Pairs of 27 = (1, 27), (3, 9)
From the aforementioned list, we can depict that, 3 when paired with 9 results in producing 27 as the result of the multiplication.
Therefore the value of x is given as:
x = 9
Images/mathematical drawings are created with GeoGebra.
