JUMP TO TOPIC
Factors of 26: Prime Factorization, Methods, Tree, and Examples
Factors of 26 refer to the numbers that may completely divide 26 or the numbers whose product, when two numbers are multiplied together, is 26. Therefore, if a number divides 26 without a remainder, it is named as a factor of 26.

Figure 1 – All possible Factors of 26
To find the factors of the number you are looking for, list all the numbers that are less than or equal to the number you are looking for. The numbers for 26, for instance, will range from 1 to 13. Then, one can find the answer by splitting each of them in half. A fascinating fact regarding factors is that two is the factor of all numbers.
Both division and Multiplication are the two ways to figure out a number’s factors.
The factors of a number can be discovered in a variety of ways, though. There is a strategy to find the factors of an even number. To find the factors, keep dividing the number by smaller numbers.
The numbers that are completely divisible and leave zero remainders are called their factors. Let’s consider the following example to understand the concept better.
26 divided by two will give in a result of 13. In this case, both the divisor and quotient are considered as the factor of 26. The quotient and divisor can also be written in the form of factor pairs as (2, 13).
This article is your guide on how to find out the factors of 26, factor pairs, factor trees, simple solutions, and much more. Once you know how to determine the factors of 26 through this article, finding out the factors of any other number will be a piece of cake for you!
What Are the Factors of 26?
The factors of 26 are 1, 2, 13, and 26. Thus, 26 is a composite and even number.
The total number of factors is 4. (1, 26) and (2, 13) are the factor pairs of 26. It can be accomplished by pairing the integers so that the outcome is 26. When you divide these numbers by 26, the result is always 0.
How To Calculate the Factors of 26?
You can calculate the factors of 26 by using the Multiplication and division method. These two techniques can be easily manipulated, as discussed previously.
Let’s start by discussing how to determine the factors by dividing. Look up all the numbers less than or equal to 26. Next, divide each of the numbers by 26. The divisors that result in a remainder of 0 are the factors of 26.
To grasp this concept, let’s look at the following example:
We divide 26 by 2, the smallest factor of 26 other than one, and get 13. Therefore, 2 and 13 are the factors of the number 26.
\[ \frac{26}{2} = 13 \]
This shows that both divisor and quotient (2 and 13) are factors of 26 because the quotient is a whole number with zero remainders.
Below is a list of all the factors of 26:
\[ \frac{26}{1} = 26 \]
\[ \frac{26}{2} = 13 \]
\[ \frac{26}{13} = 2 \]
\[ \frac{26}{26} = 1 \]
Therefore, all the factors are 1, 2, 13, and 26.
Let’s now concentrate on multiplying to discover the factors of 26. In all possible scenarios, consider the number 26 to be the result of two whole numbers. In each of these products, every single integer is a factor of 26.
For example:
1 x 26 = 26
2 x 13 = 26
13 x 2 = 26
26 x 1 = 26
Hence, these are the factors of 26, i.e., 1, 2, 13, and 26.
Factors of 26 by Prime Factorization
One technique to express a particular number as the product of its prime factors is the method of prime factorization, which involves determining which prime factors can multiply
with one another to yield the number as a product. In other words, it is the method of finding or expressing the given number as the product of prime numbers.
A prime number only has two factors: one and the number itself. Given that 26 is a composite number, it should have prime components.
Below is a process for determining the prime factors of 26:
The first method is to write the number 26 down and multiply it by its pair factor (2, 13). Secondly, the pair factor (2, 13) cannot be further divided because the numbers 2 and 13 are both prime numbers.
Now, multiply two by 13 to get the prime factors. As a result, the prime factors of 26 are represented as the product of 2 and 13.
For denoting the prime factors of 26, the notations 2×13 are used. Prime numbers 2 and 13 are those in this example.
The diagram of this number Prime Factorization is attached below:
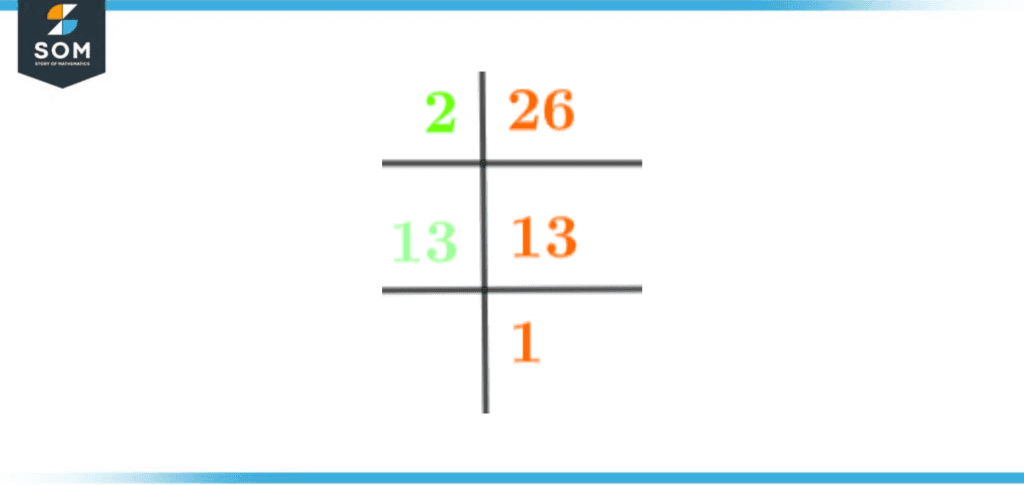
Figure 2 – Prime Factorization of 26
Factor Tree of 26
Even the factors of a number can be stated in various ways. The prime factors of a number can be graphically represented in multiple ways, one of which is by expressing factors as a Factor tree. The actual number serves as the root of the factor tree, and the branches that sprout from it represent factors until you reach the prime number.
The diagram of the Factor Tree of this number can be seen below:
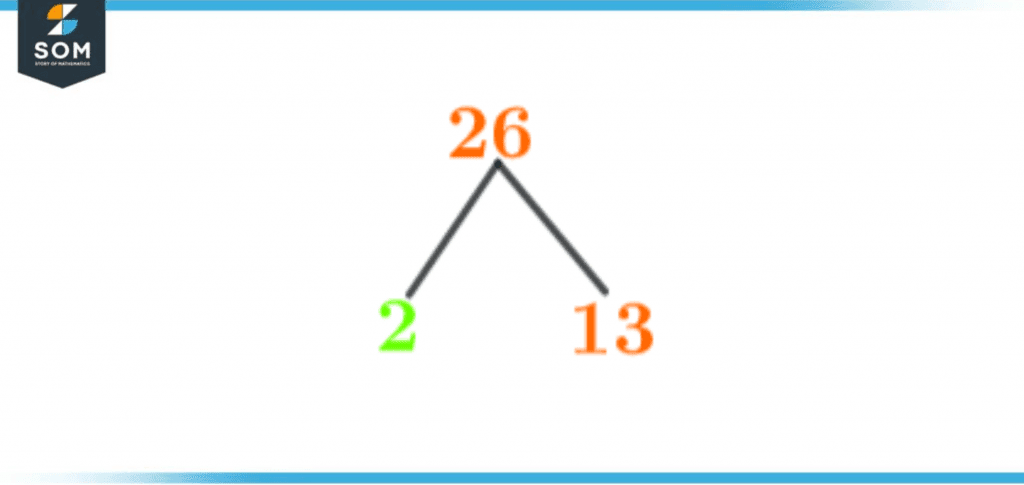
Figure 3 – Factor Tree of 26
As a result, according to prime factorization, 2 and 13 are 26’s prime factors. Following are the super fun and interesting facts about the number 26:
- There are 26 ways to connect 5 locations using pairwise connections, making it a phone number. Also, there are 26 sporadic groups.
- The smallest number that falls into both categories of Non-totient and non-cototient is 26.
- The face count on a rhombicuboctahedron is 26. Moreover, a 26-sided polygon is also referred to as an icon hexagon.
- In chemistry, 26 is the atomic number of iron, and in bosonic string theory, there are 26 spacetime dimensions.
- 26 represents Z, the final letter in the English alphabet. Furthermore, there are 26 counties in the Republic of Ireland.
- A television show’s annual episode count used in the United States of America is 26. Also, the 26th President of the USA was Theodore Roosevelt.
- There are 26 red cards and 26 black cards in a standard deck of cards. 8. The number of bones that make up a typical human foot and ankle is 26. 9. 26 is the name of an alternative rock group from Australia, and the number of letters in the Latin alphabet is also 26.
- During the 1930s to 1950s, dice game was quite common in the Midwest of the United States. To win, players had to roll a specific number 26 or more, precisely thirteen times, or fewer than 10.
- There are 26 holes in a floorball ball, and the number of total miles in a marathon is 26.
Factors of 26 in Pairs
A Factor pair is referred to as a set of two integers; when multiplied together, they yield the number itself as the outcome. The factors are as follows:
If 1 × 26 = 26, then (1, 26) is a pair factor of 26.
Similarly, let us find another pair.
1 × 26 = 26, (1, 26) is a pair factor of 26
2 × 13 = 26, (2, 13) is a pair factor of 26
13 × 2 = 26, (13, 2) is a pair factor of 26
26 × 1 = 26, (26, 1) is a pair factor of 26
These are the positive factor pairs of 26. Reversing the signs is all that is necessary to determine the negative factor pair. The following are the negative factor pairs:
If -1 × -26 = 26, then (-1, -26) is a pair factor of 26.
-1 × -26 = 26, (-1, -26) is a pair factor of 26
-2 × -13 = 26, (-2, -13) is a pair factor of 26
-13 × -2 = 26, (-13, -2) is a pair factor of 26
-26 × -1 = 26, (-26, -1) is a pair factor of 26
Thus, these are the opposing factor pairs of the integer 26.
Factors of 26 Solved Examples
Example 1
Find the common elements between 26 and 24.
Solution
Factors of 26: 1, 2, 13 and 26
Factors of 24: 1, 2, 3, 4, 6, 8, 12 and 24
So, the common factors between 26 and 24 are 1 and 2.
Example 2
There are 26 pupils in Mr. Hemsworth’s class. To offer the class some math practice, he wants to break them into groups. How many different combinations can he create with 26 students?
- No more than one student from the class can be in a group.
- The number of pupils in each group is equal.
Solution
As previously mentioned, 1, 2, and 13 are the elements of 26. However, neither all students nor one can be in the groupings. Therefore we disregard 1 and 26. As a result, she can only divide them into groups of 13 kids. Additionally, she can form two groups.
Example 3
What is the sum of all the factors of 26?
Solution
The factors of 26 are 1, 2, 13, and 26.
The answer is 42.
1 + 2 + 13 + 26 = 42
All images/ mathematical drawings are created with GeoGebra.
