JUMP TO TOPIC
Factors of 30: Prime Factorization, Methods, Tree, and Examples
Factors of 30 are a set of integers that give zero as a remainder when 30 is divided from them. Not only do these numbers give zero as a remainder but they also yield a whole number quotient when 30 is divided from them.
Figure 1 – All factors of 30
1 x 30 = 30
But 1 and 30 are not the only factors of 30. In this article, we will be diving into the details of the factors of 30 and the various techniques and methods which can be used to evaluate these factors.What Are the Factors of 30?
Factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30. When these numbers act as the divisors, they produce zero as the reminder.The number 30 is an even composite number, meaning that it consists of more than 2 factors. Also, the number 30 has 8 factors in total.How To Calculate the Factors of 30?
You can calculate the factors of 30 through various techniques such as division. Let’s take a look at the division method first. The division method states that when a number acts as the divisor, it should produce a whole number quotient and zero as the remainder.If these two conditions for the number are met, only then the number can act as the factor.In the case of the number 30, since it is an even composite number so that means that the number is divisible by 2. Let’s take a look at its division from the number 2:\[ \frac{30}{2} = 15 \]This division produced zero as a remainder and a whole number quotient which indicates that 2 is a factor of 30. Another rule of the division method is that for such divisors, which produce zero as the reminder, their quotient also acts as the factor.So in this case, 15 is also a factor of 30, since it is a quotient produced by the division of 2. Let’s take a look at the division of 30 by 15:\[ \frac{30}{15} = 2 \]Hence, both 2 and 15 are factors of 30. Let’s take a look at some other factors of 30.\[ \frac{30}{3} = 10 \]\[ \frac{30}{3} = 3 \]So, both 3 and 10 act as the factors of 30.Similarly, consider the following division:\[ \frac{30}{5} = 6 \]\[ \frac{30}{6} = 5\]So 5 and 6 are also the factors of 30.And lastly, let’s take a look at the following division:\[ \frac{30}{1} = 30 \]\[ \frac{30}{30} = 1 \]So, both 1 and 30 are also factors of 30. Hence in total, the number 30 has 8 factors and these factors are mentioned below:Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30Factors of 30 by Prime Factorization
Prime factorization is one of the unique ways to determine the factors of a number. In prime factorization, a number is broken down with the help of prime numbers and this division continues until 1 is achieved at the end.Prime factorization is the technique that is used to determine the prime factors of a number. Prime factors are those factors that are also prime numbers. In prime factorization, the division process continues until 1 is received as the end result. The prime factorization of the number 30 occurs in the following manner:\[ \frac{30}{2} = 15 \]\[ \frac{15}{5} = 3 \]\[ \frac{3}{3} = 1\]The prime factorization of the number 30 is also shown in figure 1 given below: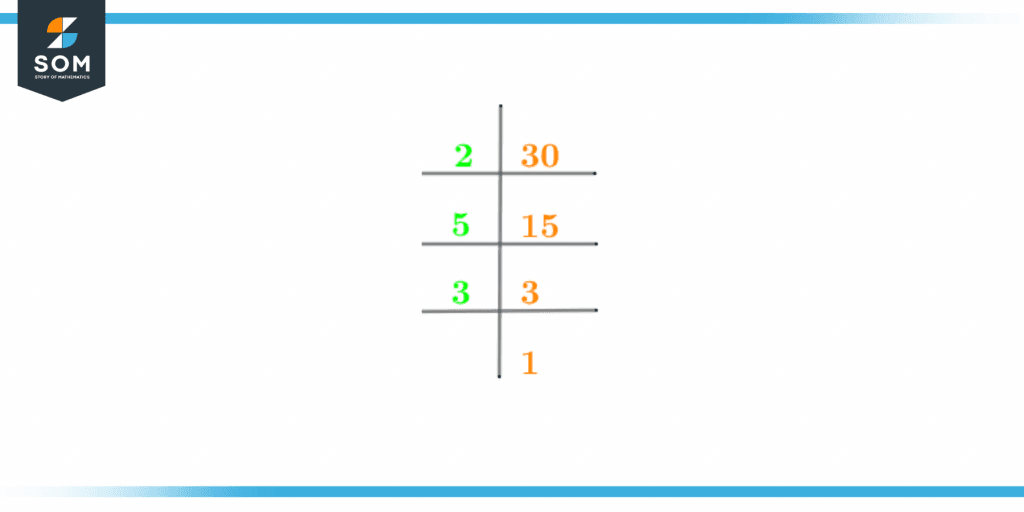
Figure 2 – Prime Factorization of 30
30 = 2 x 3 x 5
Factor Tree of 30
A factor tree is a pictorial method of representing the prime factorization of a number. The unique aspect that distinguishes factor tree from prime factorization is that instead of ending the division process at 1, the division process ends at prime numbers. The factor tree begins with the number itself and then extends out its branches to possible divisors and quotients. At the end branches, prime numbers are obtained. The factor tree of the number 30 is shown below: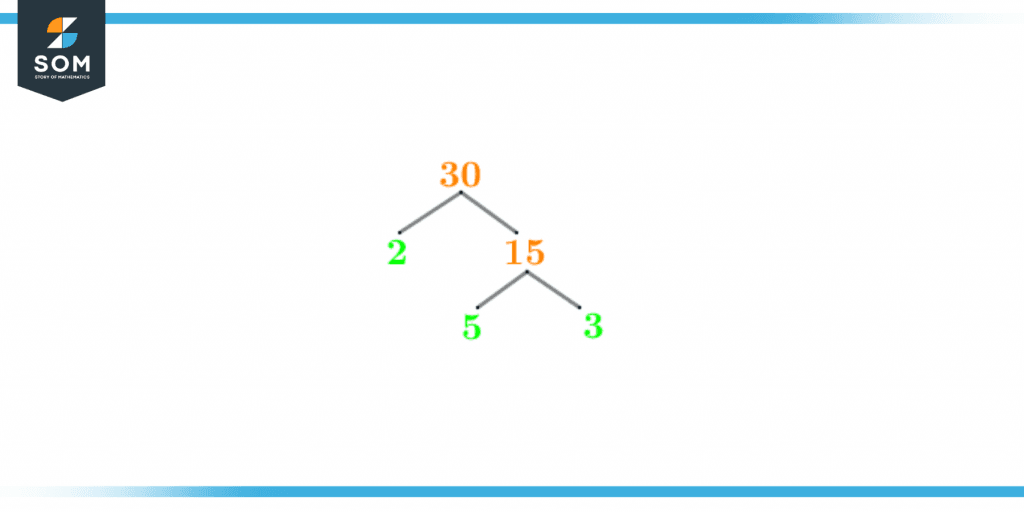
Figure 3 – Factor tree of 30
Factors of 30 in Pairs
Factor pairs, as mentioned above, are the two possible numbers that when multiplied together give the original number as the product. The factor pairs for any number can be found by the multiplication method. A factor pair simply consists of a factor of a number and its whole number quotient. The factor pairs of 30 are given below:2 x 15 = 30
1 x 30 = 30
3 x 10 = 30
5 x 6 = 30
Hence, the factor pairs of 30 are (1,30), (2,15), (3,10), and (5,6).These factor pairs can also consist of negative factors. They are pretty much the same as the positive factors only the reversed signs are different. The condition for negative factor pairs is that both the factors existing in the pair must have the negative sign.The negative factor pairs of 30 are (-1,-30), (-2,-15), (-3,-10), and (-5,-6).Factors of 30 Solved Examples
To further enhance the concept of the factors of 30, let’s take a look at some simple solved examples constituting the factors of 30.Example 1
Calculate the product of all the prime factors of 30.Solution
To calculate the product of all the factors of 30, let’s first list down the factors of 30.Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30 According to the prime factorization of 30, the following prime factors were obtained:Prime factors of 30 = 2, 3, 5Now, to calculate the product of these prime factors, simply multiply them together. Their multiplication is shown below:30 = 2 x 3 x 5
Hence the product obtained is 30.Example 2
Find the average of all the factors of 30.Solution
To find the average of all the factors of 30, let’s first note down the factors of 30.Following are the factors of 30:Factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30Calculating the average of these factors by using the following formula:\[ Average = \frac{\text{Sum of numbers}}{\text{Total numbers}} \]\[ Average = \frac{1+2+3+5+6+10+15+30}{8} \]\[ Average = \frac{72}{8} \]Average = 9
Hence, the average of all the factors of 30 is 9.