JUMP TO TOPIC
Factors of 300: Prime Factorization, Methods, Tree, and Examples
The factors of 300 are the set of 18 natural numbers that give off zero as the remainder whenever they act as the divisors for the number 300. Apart from producing zero as the remainder, these numbers also result in a whole number quotient.
Figure 1 – All possible Factors of 300
What Are the Factors of 300?
The factors of 300 are the following: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, and 300. All these numbers make 300 completely divisible when they act as the divisors.In total, the number 300 has 18 factors. These 18 factors can also be split into nine 9-factor pairs.How To Calculate the Factors of 300?
You can calculate the factors of the number 300 through the division method. This method is pretty simple and always yields accurate results. This method is entirely based on the mathematical operation of division.The number 300 is a significant number, so it’s easier to determine the factors of this number by first determining the range in which these factors lie. This range starts from the smallest factor, one, and goes to half of that number.Since half of 300 is 150, the range of factors of 300 will be between 1 and 150. Moreover, the number 300 is an even number and ends at a zero, indicating that the numbers 2, 5, and 10 will automatically be the factors of this number.Now that we have the range of these factors, let’s move on to the application of the division method on the number 300. The divisions of the factors of 300 are shown below:\[ \frac{300}{1} = 300 \]\[\frac{300}{2} = 150 \]\[ \frac{300}{3} = 100 \]\[ \frac{300}{4} = 75 \]\[\frac{300}{5} = 60 \]\[ \frac{300}{6} = 50 \]\[ \frac{300}{10} = 30\]\[\frac{300}{12} = 25 \]\[\frac{300}{15} = 20 \]\[ \frac{300}{20 } =15 \]\[\frac{300}{25} = 12 \]\[ \frac{300}{30} = 10 \]\[ \frac{300}{50} = 6\]\[\frac{300}{60} = 5 \]\[\frac{300}{75} = 4 \]\[ \frac{300}{100} = 3 \]\[\frac{300}{150} = 2 \]\[ \frac{300}{300} = 1 \]Therefore, the list of all the factors of 300 is given below:Factors of 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, and 300.As these numbers are natural numbers, so it’s natural for them to have negative integers as well. This gives birth to the concept of negative factors. The negative factors are the same as positive ones, but they only have the opposite sign.The negative factors of 300 are given below:Negative Factors of 300: -1, -2, -3, -4, -5, -6, -10, -12, -15, -20, -25, -30, -50, -60, -75, -100, -150, and -300Factors of 300 by Prime Factorization
The prime factorization method is an extension of the division method but is only used to determine the prime factor factors. Prime factors can be regarded as prime factors. The prime factorization is based on division operation.In prime factorization, the division is continued with the help of prime numbers only in order to obtain the prime factors. The division continues until only one is left at the end.The prime factorization for the number 300 is shown below:300 $\div$ 5 = 60
60 $\div$ 5 = 12
12 $\div$ 2 = 6
6 $\div$ 2 = 3
3 $\div$ 3 = 1
As one is achieved, that concludes the prime factorization. This prime factorization can be mathematically expressed as follows:Prime Factorization of 300 = 5 x 5 x 2 x 2 x 3
OrPrime Factorization of 300 = $5^{2}$ x $2^{2}$ x 3
The prime factorization of the number 300 is shown below in figure 1: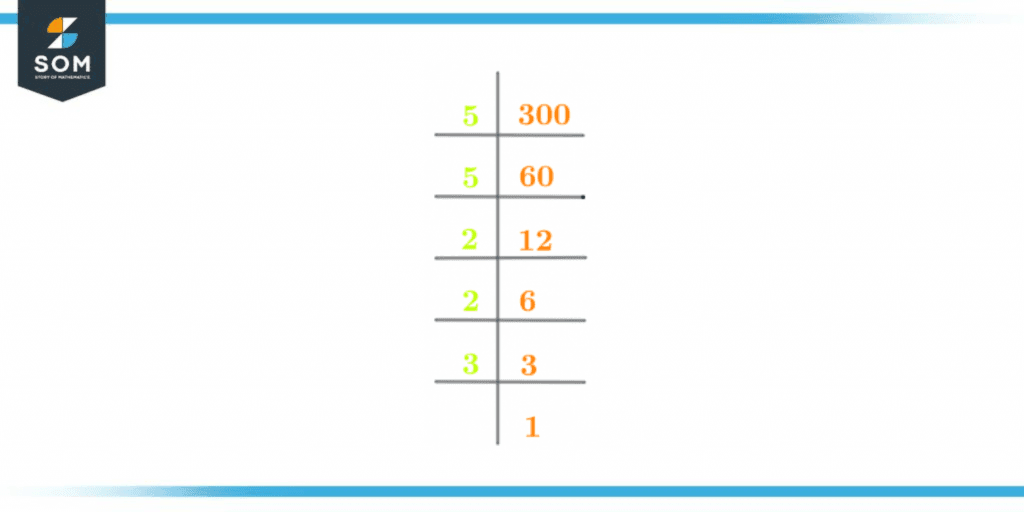
Figure 2 – Prime Factorization of 300
Prime Factors = 2, 3, 5
Factor Tree of 300
The factor tree is the visual representation of the prime factorization method since it is the pictorial depiction of prime factorization, indicating that the factor tree is also based on the division operation and is used to determine the prime factors.The factor tree gained its name from the fact that its structure resembles a tree. One branch of the factor tree will always hold a prime number.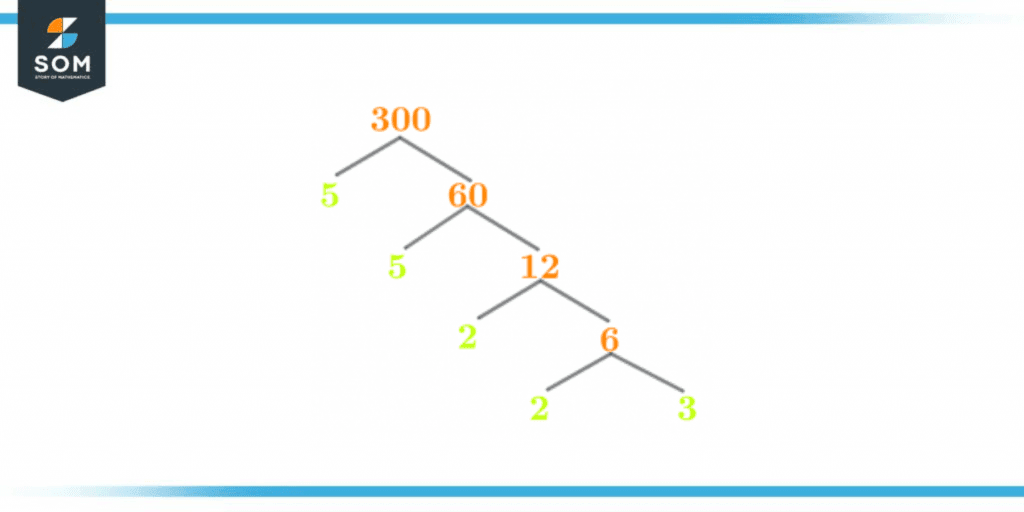
Figure 3 – Factor Tree of 300
Factors of 300 in Pairs
A factor pair is a pair of numbers that not only act as the factors but also produce the original number as the result when they are multiplied by one another. Within a factor pair, two numbers can exist.The factors of 300 can be determined through the division method. This method also has an extension known as the prime factorization method, which only deals with determining the prime factors. These factors can also be arranged in the form of a factor tree and can be evenly divided into factor pairs.
The condition for the factor pair is that both numbers must be the factors of the original number, and they must produce the actual number as the product when multiplied. The factor pairs of the number 300 are given below:1 x 300 = 300
2 x 150 = 300
3 x 100 = 300
4 x 75 = 300
5 x 60 = 300
6 x 50 = 300
10 x 30 = 300
12 x 25 = 300
15 x 20 = 300
So the positive factor pairs of 300 are given as follows:(1, 300)
(2, 150)
(3, 100)
(4, 75)
(5, 60)
(6, 50)
(10, 30)
(12, 25)
(15, 20)
As for the number 300, negative factors also exist, so the same is applied to the factor pairs. The negative factor pairs of the number 300 are given below:-1 x -300 = 300
-2 x -150 = 300
-3 x -100 = 300
-4 x -75 = 300
-5 x -60 = 300
-6 x -50 = 300
-10 x -30 = 300
-12 x -25 = 300
-15 x -20 = 300
The negative factor pairs are as follows:(-1, -300)
(-2, -150)
(-3, -100)
(-4, -75)
(-5, -60)
(-6, -50)
(-10, -30)
(-12, -25)
(-15, -20)
Factors of 300 Solved Examples
To learn more about the factors of 300, let’s take a look at some simple yet detailed examples on the factors of 300 given below.Example 1
Calculate the sum of all the factors of 300 and determine if the resulting number is a multiple of 2.Solution
To begin with, the solution of calculating the sum of all the factors of 300, let’s first list down these numbers. There are 18 factors of 300 in total, and these are given below:Factors of 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, and 300Calculating the sum of all these factors of 300:Sum of factors of 300 = 1 + 2 + 3 + 4 + 5 + 6 + 10 + 12 + 15 + 20 + 25 + 30 + 50 + 60 + 75 + 100 + 150 + 300
Sum of factors of 300 = 568
The resulting number, 568, is an even number. Since it is an even number, this number will be a multiple of 2.This is evident from the multiplication shown below:2 x 284 = 568
Hence, the result obtained from the sum of all factors of 300 is a multiple of 2.Example 2
Separate the even and odd factors of 300.Solution
The factors of 300 are given below:Factors of 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, and 300
Now, let’s separate the even and the odd factors.The even factors of 300 are given below:Even Factors of 300 = 2, 4, 6, 10, 12, 20, 30, 50, 60, 100, 150, and 300
Now, let’s list the odd ones. These are given below:Odd Factors of 300 = 1, 3, 5, 15, 25, and 75
All images/mathematical drawings are created with GeoGebra.