JUMP TO TOPIC
Factors of 31: Prime Factorization, Methods, Tree, and Examples
Factors of 31 are those numbers that divide 31 perfectly without leaving a remainder. Therefore, if a number divides 31 with a 0 as the remainder, it is considered a factor.

Figure 1 – All possible Factors of 31
This article will cover every detail about factors, including calculating the factors of 31, clear and straightforward solutions, entertaining facts, prime factorization, and all about factor pairs.
What Are the Factors of 31?
Factors of 31 are 1 and 31; the fact that 31 is a prime number means that the only two possible factors are 1 and 31.
The factor pairs are (1, 31) and (31, 1). You can achieve this by pairing the number in such a way that the result is 31. We also know that the factors of the number 31 are its actual divisors.
How To Calculate the Factors of 31?
To calculate the factors of 31, there are two methods, i.e., Division and Multiplication.
When finding the factors through division, the first step is to list every integer lower than 31. After that, multiply each figure by 31. Its factors are the divisions of 31 that result in a remainder of 0.
The examples below will provide you with a greater understanding of this concept:
The lowest factor of all the numbers, i.e., 1, can be used to divide the number 31. Consequently, factors of 31 are 1 and 31.
\[ \frac{31}{1} = 31 \]
So the quotient is a whole integer and has no remainder; it is shown that the divisor and the quotient are both factors of 31.
To analyze factors, create a list of all the numbers that are less than or equivalent to the number you are looking for factors of. The numbers for 31, for example, will be from 1 to 31.
If so, the answer can be found by dividing each of them. The fact that odd number factors do not have two as one of their factors is noteworthy. There are various approaches to finding integer factors.
Multiplication and division can be used to find the factors of a number. However, one of the straightforward means to determine factors is to divide the given number itself until there is no remainder.
At this point, the quotient and divisor are considered to be factors of the original number. Consider one of these scenarios as an example. 31 divided by 31 yields a value of 1. As a result, the solution and the divisor are both considered factors. Together, they are referred to as factor pairs, i.e. (31, 1).
Now let’s begin concentrating on multiplication to identify the factors of 31. In all likely scenarios, take 31 as the sum of two whole numbers. Each of these products contains only integers that are factors of 31.
Look at these examples:
1 x 31 = 31
31 x 1 = 31
Factors of 31 by Prime Factorization
Prime factorization is representing a number by a group of factors multiplied collectively. To put it more simply, it is a method for determining or showing a given integer as the sum of prime integers.
Suppose we divide 31 by 2 or 3 or 5 or 7 and so on. We will get a decimal number as the answer, which depicts that they can never be factors. For them to be factors, the answer should be a whole number.
The only two factors that make up a prime number are one and the number itself. Therefore, since 31 is a prime number, it cannot be factorized further.
As in the case of 1, it is neither a prime number nor a composite number. Hence, we conclude that the prime factorization of 31 is 31.
The image below shows the prime factorization of the prime number 31:
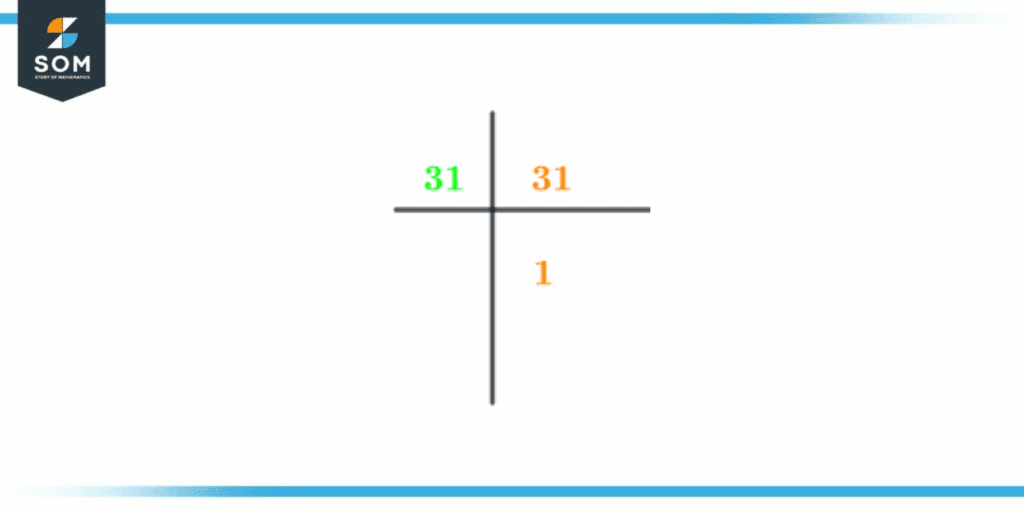
Figure 2 – Prime Factorization of 31
Factor Tree of 31
A Factor Tree is a method for figuring out the prime factors of any number. Finding factors of a number is just like finding someone’s ancestors. The root of the factor tree is the actual number, and until you get to the prime number and until you get to the prime number, the branches that come out of the root are factors.
Let’s proceed with 20 as a factor tree example before moving on to the factor tree of 31. We will look for two numbers that, when multiplied together, produce the number 20. We shall divide 20 into either of its two factors, 4 or 5.
Finding the factors of 4 and 5 is what we will do next. 4 can be written as 2 x 2, so we will put those factors into the tree under 4. Both 5 and 2 are prime numbers, so they cannot be divided further because a prime number consists of only two factors: itself and the number 1.
The illustration of the factor tree for number 31 is shown below:
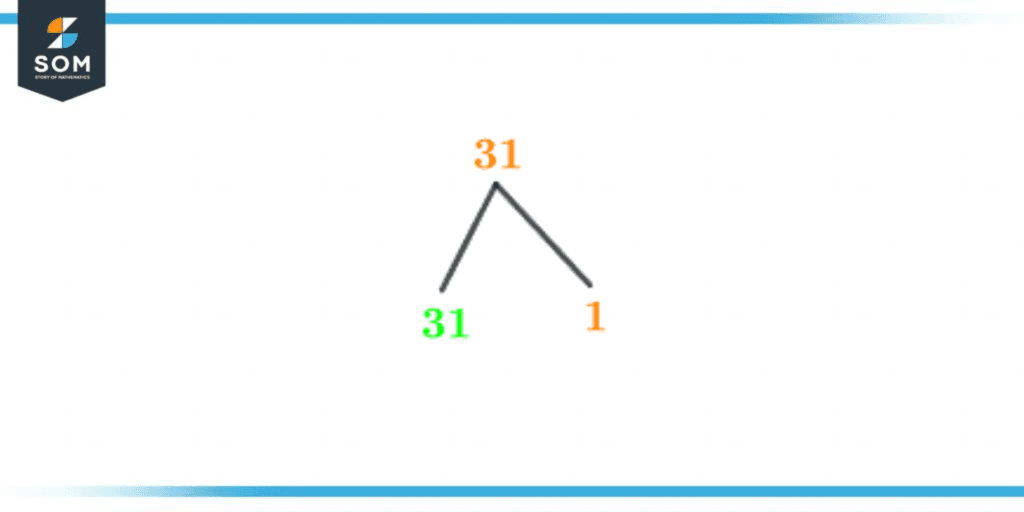
Figure 3 – Factor Tree of 31
The following fascinating information about prime number 31 is provided for your amusement:
- 31 regular polygons have odd numbers of sides.
- The number 31 is the first prime centered pentagonal, the first centered decagonal, and the eighth happy number.
- The value of pi to four significant figures is the cube root of 31.
- There are seven months out of 12 whose day count is 31, i.e., January, March, May, July, August, October, and December.
- Halloween and New Year’s Eve are celebrated on 31st October and 31st December, respectively.
- 31 is the country code when calling the Netherlands directly from abroad.
- The number of flavors offered by Baskin-Robins in Japan is 31. Moreover, the stores are also known as “31 Ice cream”.
Factors of 31 in Pairs
Factor Pair refers to two integers that are multiplied together to create the number itself. The positive factor pairs of 31 are given below:
1 x 31 = 31, (1, 31) is a pair factor of 31.
31 x 1 = 31, (31, 1) is a pair factor of 31.
Negative pair factors are also possible because any two negative numbers can be multiplied to generate a positive value. The negative factor pair can be identified by simply changing the signs. The pairs of negative factor pairs are listed below:
-1 x -31 = 31, (-1, -31) is a pair factor of 31.
-31 x -1 = 31, (-31, -1) is a pair factor of 31.
Therefore, stated above are the positive and negative factor pairs of 31.
Factors of 31 Solved Examples
Example 1
Today Eloise received her class test results. In her exam, she scores an 8 out of 10. The question she did wrong was, “Is 31 a prime number or a composite number? Give the right response and justification.”
For future exams, help her fix her mistake.
Solution
Prime numbers are those whose factors are one and the number itself, whereas composite numbers have more than two factors.
The statement above clearly means that 31 is a prime number because it has only two factors, i.e., 1 and 31.
Example 2
Ali has a mango tree in his backyard since he loves mangoes. This summer, his mango tree produced a harvest equivalent to the sum of all the factors 31.
To determine the number of mangoes that grew in Ali’s backyard, choose from the options below the correct factors of 31 and add them.
- 1, 3 and 11
- 1 and 31
- 1, 11, and 31
Solution
Option b is correct, as 31 has only two factors which are 1 and 31.
1 + 31 = 32
Thus, 32 mangoes were grown this summer on Ali’s mango tree.
Example 3
Peter was playing treasure hunt at a friend’s birthday bash. He had to follow the instructions on the piece of paper he had discovered in order to find the treasure.
It was written on the paper: “ You shall find the common factors between 31 and 93. Add them and then tell the answer to the party’s host, who will undoubtedly lead you to the treasure”.
By figuring out the common factors between 31 and 93 and adding them, you can assist Peter in finding the treasure.
Solution
The two factors of the number 31 are 1 and 31.
The factors of 93 are as follows: 1, 3, 31, and 93.
Hence, the common factors are 1 and 31.
31 + 1 = 32
Thus, Peter will tell the party’s host that the correct answer is 32.
All images/diagrams are made using GeoGebra.
