JUMP TO TOPIC
Factors of 38: Prime Factorization, Methods, Tree, and Examples
The factors of 38 are any integers smaller than 38 which divides 38 without leaving any remainder. In other words, it can be any integer smaller than 38, which multiplies with another integer to give us the result of 38.
Figure 1 – All possible Factors of 38
What Are the Factors of 38?
The factors of 38 are 1, 2, 19, and the number 38 itself. These are the only numbers to divide 38 fully without leaving any remainder. Any other integers smaller than 38 would not be able to give us the same results. This data also proves that 38 is a composite number as it has more than two primary factors. In total, there are only four factors of 38.How To Calculate the Factors of 38?
To find out the factors of any number, two methods can be used; the first one is multiplication and the second one is division. Both methods are straightforward and reliable for calculating the correct answers.You only have to be cautious about considering every single number on your list for working. You might lose a score if the number you missed is a factor for your given number. Let’s start with the division method. For this, we will first half the given number. This will save us time as integers larger than half of the given number can never be the factor of that number except for the number itself. We will consider all integers between 1 and that number and start dividing the given number by those integers. The integer that can divide the given number fully, without leaving any remainder, will be a factor along with the quotient for that number. Let’s look at the example of 38 to understand this concept better:To get the half of 38, we will divide it by 2. This will give us 19. Now we will start to divide 38 by numbers between 1 and 19. Upon dividing 38 by 2, we get 19 as the quotient, and nothing is left as the remainder. Now both 2 and 19 (the divisor and the quotient) are considered as the factors of 38. When we repeat this process with other numbers, none of them can divide 38 fully. So our factors of 38 will be 1, 2, 19, and 38.For calculating factors by the multiplication method, we will try multiplying different integers together. Our goal here is to get 38 as the product of multiplication. If any pair of the numbers make up to the product ‘38’, both integers will be considered as factors of 38. For better understanding, have a look at these examples:1 x 38 = 38
2 x 19 = 38
Since the result retrieved is 38, both the numbers will be considered product factors.Hence it is proved by both of these methods that 1, 2, 19, and 38 are the only factors of 38.Factors of 38 by Prime Factorization
Prime factorization can be called a decomposition method as a number is decomposed into its factors until prime factors are not achieved. It is done to know the prime factors of an integer.For this method, we will start by dividing the given number with the smallest number, except for 1, which divides our given number fully. Like in the case of 38, we will start by dividing 38 by 2, and our answer will be 19.For 38, our work will stop here as the results achieved were prime numbers. So we know that the prime factors of 38 are 2 and 19. To represent this answer, we can use the notation 2 x 19.You can take a look at the Prime Factorization of 38 below: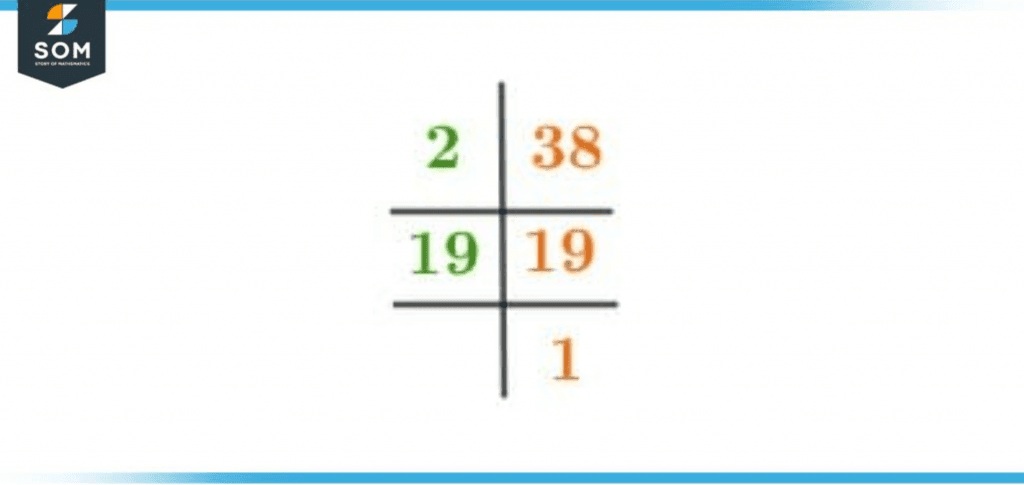
Figure 2 – Prime Factorization of 38
Factor Tree of 38
A factor tree is one method to represent a number’s factors. Apart from representing prime factorization in notations form, a factor tree can also be used. In a factor tree, the given number for the method is written on the top. It is divided by a small number first, and the answers are written below by extending the branches. This process continues until prime numbers are not achieved. The tree ends with prime numbers at the bottom.For the factor tree of 38, we will write 38 on top. Then we will start dividing 38 by smaller divisible numbers first. Remember that we won’t divide it by 1. Another smaller divisible number is 2, so we will divide 38 by 2. We will get 19 as our answer. Now we will extend one line below 38 and write one below it; then, we will open another line similarly and write 19 below it. Since both numbers are prime numbers, we have reached the end of the factor tree. So the factor tree of 38 will end here. A factor tree of 38 will be attached by the end of this article. You can look at it to comprehend this knowledge with the actual representation of the factor tree. The diagram of the Factor Tree of 38 is attached below: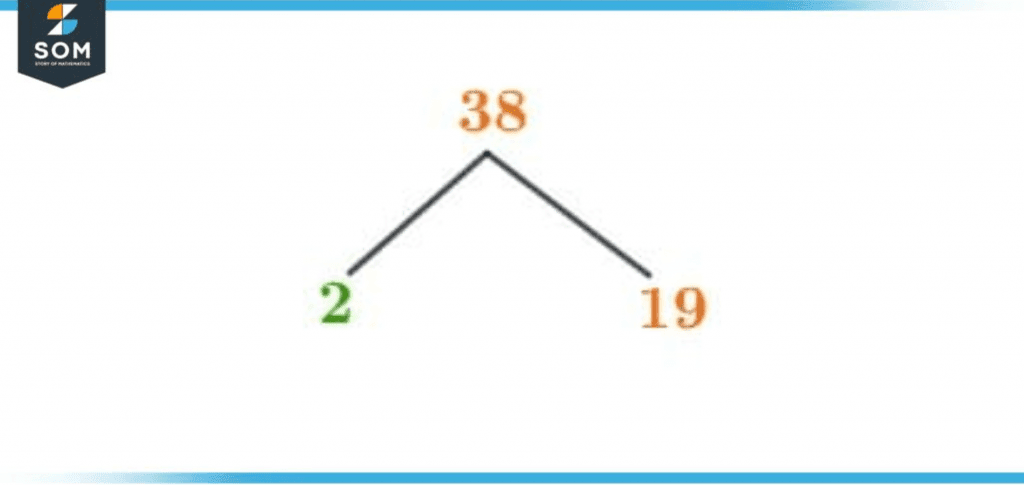
Figure 3 – Factor Tree of 38
Factors of 38 in Pairs
Any two numbers which multiply to give you a product of any given number form a factor pair of that number. These numbers can be positive or negative, but they cannot be decimals or fractions.Earlier in this article, when we learned to calculate factors through the division method, we found that both the divisor and quotient are considered factors. Now for this concept, we will pair both of those numbers together to form a factor pair of that given number.The first step in finding the factor pairs is to know whether the given number is a prime number or a composite number. If it is a prime number, both actors will be paired together to make a factor pair.On the other hand, if the number is composite, you will have to start by multiplying its factors with each other to find a pair that gives you the product of that given number. This can be a little time-consuming for numbers with many factors as they will have many factor pairs. For finding factor pairs of 38, we will make a list of its factors first, as shown below:Factor list = 1, 2, 19, 38
Looking at the factor list, we can tell it’s a composite number. Now we will multiply these numbers with each other to find out which numbers give us the product 38.1 x 2 = 2
1 x 38 = 38
2 x 19 = 38
2 x 38 = 76
38 x 19 = 722
Now that we have made a list of every possible product, we can figure out that there are only two pairs that give us the result 38. Only those two pairs, (1, 38) and (2, 19), will be considered as our answer.Factors of 38 Solved Examples
Now that we have gained enough knowledge about factors of 38 let’s look at a few solved examples to memorize the concepts.Example 1
Make a list of even factors of 38.Solution
We will look into the list of factors of 38, and then we will identify even numbers for our answer. The factors of 38 are 1, 2, 19, and 38, so our solutions will be 2 and 38.Example 2
How to determine that 38 is a composite number?Solution
Factors of 38 are 1, 2, 19, and 38. This proves it’s a composite number, as prime numbers only have two factors.Example 3
List common factors between factors 2 and 38.Solution
Factors of 2: 1 and 2
Factors of 38: 1, 2, 19, and 38.
Common factors: 1 and 2.All images/mathematical drawings are made using GeoGebra.