JUMP TO TOPIC
Factors of 384: Prime factorization, Methods, Tree, and Examples
Any natural number that can completely divide 384 with remainder zero is called the factor of the number 384. There are a total of 16 factors of 384. The number 384 is regarded as a composite number as it has more than two factors.

Figure 1 – All possible factors of 384
As 384 is a composite number, it will be having more factors as compared to any prime number, which has only two factors: 1 and the number itself. For example, 7 is a prime number so it has only two factors: 1 and 7 itself.
In this complete guide, we are going to learn how to find factors of 384 using various methods such as the division method and prime factorization. Also, we will solve some examples to better understand the concept.
What Are the Factors of 384?
The factors of 384 are the following: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128, 192, and 384.
All of them are the factors of 384 because they divide 384 without leaving any remainder behind. A number can have positive as well as negative factors, therefore the negative factors of 384 are the additive inverse of its positive factors.
Factors are useful for identifying whether the number is a prime or composite as the prime number has always two factors while a composite number can have as many factors starting from 3 up to any numbers as we go higher. One number which is neither prime nor composite is 1.
How To Calculate the Factors of 384?
You can calculate the factors of 384 using different methods such as the divisibility rule method, multiplication method, and prime factorization. Let’s discuss each method individually.
Use the Divisibility Rules
By using divisibility rules, we can find the factors of the given number. Check the divisibility of all the natural numbers starting from the smallest natural number by 384. The numbers that will pass the divisibility test, which means that nothing will be left as the remainder when divided, are called the factors of 384.
The factors of 384 are given as:
\[ \dfrac{384}{1} = 384 \]
\[ \dfrac{384}{2} = 192 \]
\[ \dfrac{384}{3} = 128 \]
\[ \dfrac{384}{4} = 96\]
\[ \dfrac{384}{6} = 64 \]
\[ \dfrac{384}{8} = 48 \]
\[ \dfrac{384}{12} = 32 \]
\[ \dfrac{384}{16} = 24 \]
\[ \dfrac{384}{24} = 16 \]
\[ \dfrac{384}{32} = 12\]
\[ \dfrac{384}{48} = 8\]
\[ \dfrac{384}{64} = 6 \]
\[ \dfrac{384}{96} = 4 \]
\[ \dfrac{384}{128} = 3 \]
\[ \dfrac{384}{192} = 2 \]
\[ \dfrac{384}{384} = 1 \]
So, all of the above-mentioned numbers are the factors of 384.
The following numbers pass the divisibility test and are called the factors of 384.
Factors of 384: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128, 192, and 384
The negative factors of 384 are given below.
Negative Factors of 384: -1, -2, -3, -4, -6, -8, -12, -16, -24, -32, -48, -64, -96, -128, -192, and -384
Important Properties
Here is a list of some of the important properties of the number 384 and its factors.
- 384 is a composite number as it has 16 factors in total.
- The number 384 is obtained as the result of the sum of two twin prime numbers that are 191 and 193.
- It has 14 even factors and two odd factors.
- The prime factorization of 384 is given as $ 2^{ 7 }$ x 3 = 384.
- 384 is the sum of six consecutive prime numbers which are 53, 59, 61, 67, 71, and 73.
Factors of 384 by Prime Factorization
Prime factorization is the method of finding the prime factors of the given number in this case it is 384. It is also called prime factorization because all the factors found using this method are prime numbers.
Prime factorization can be determined using the repeated division method or factor tree method.
Using Repeated Division Method
Using the repeated division method, we are solving the number 384, where 384 is the dividend and starts from prime number 2 as the divisor. 384 divided by 2 gives us 192, 192 divided by 2 gives us 96, 96 divided by 2 gives us 48, 48 divided by 2 gives us 24, 24 divided by 2 gives us 12, 12 divided by 2 results 6 and 6 divided by 2 gives 3.
The prime factorization of 384 is shown below:
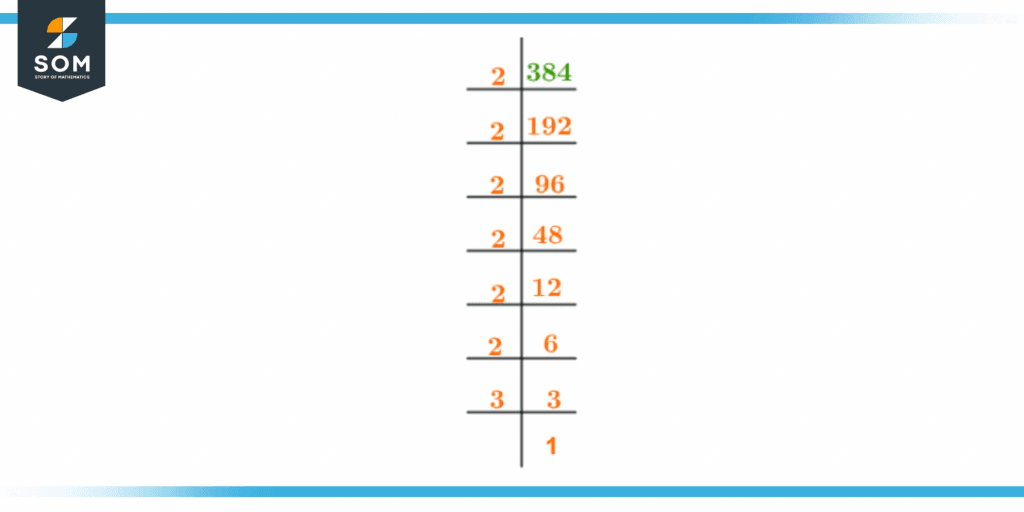
Figure 1 – Prime factorization of 384
So, the prime factorization of 384 can be expressed as:
2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 = 384
$2 ^{7}$ x 3 = 384
Factor Tree of 384
The factor tree of 384 is illustrated in figure 2 below:
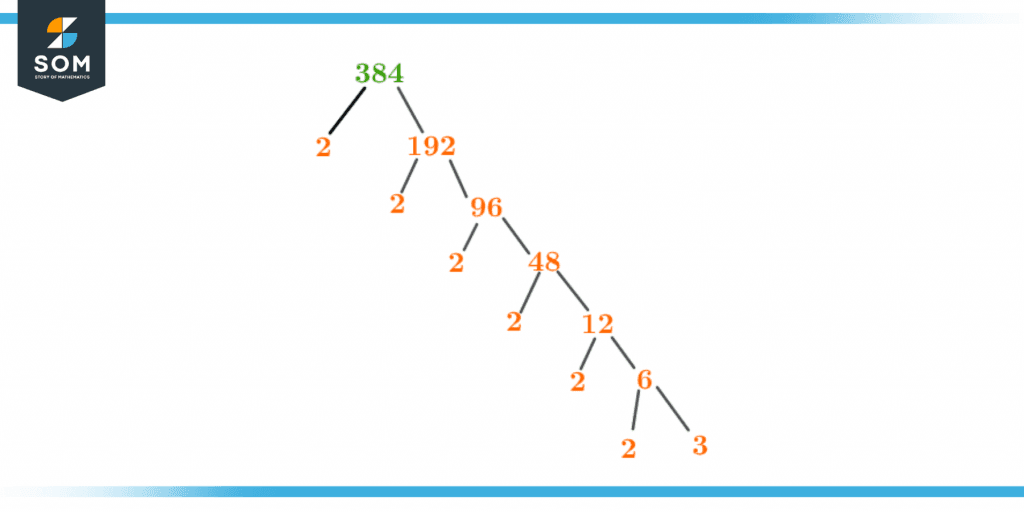
Figure 2 – Factor Tree of 384
Factors of 384 in Pairs
The factors of a given number are written in pairs such that when both the numbers are multiplied, the product is the given number. The pairs are called the factor pairs of the number.
The factor pairs of 384 are given as:
1 x 384 = 384
2 x 192 = 384
3 x 128 = 384
4 x 96 = 384
6 x 64 = 384
8 x 48 = 384
12 x 32 = 384
16 x 24 = 384
24 x 16 = 384
Therefore, the factor pairs of 384 are (1, 384), (2, 192), (3, 128), (4, 96), (6, 64),(8, 48), (12, 32), and (16, 24).
There are 8 positive factor pairs of 384. Similarly, there are also 8 negative factor pairs, which are the additive inverse of the positive factors.
Factors of 384 Solved Examples
Following are some solved examples involving the factors of 384.
Example 1
Stephen bought 24 packets of chocolates. Each packet contains 16 chocolate candies. How many candies are there in total?
Solution
Total number of packets = 24
Each packet contains = 16 chocolates
Total number of chocolates = 16 x 24
Total Chocolates are = 384
Example 2
What is the greatest factor in the factor list of 384?
Solution
The greatest factor in the list of factors 384 is 384.
Example 3
Find the common factors of 384 and 16.
Solution
The factor list of 384 is given below.
Factors of 384: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 128, 192, and 384
The factors 16 are given in the list below.
Factors of 16: 1, 2, 4, 8, and 16
The common factors are 1, 2, 4, 8, and 16.
Images/mathematical drawings are created with GeoGebra.
