JUMP TO TOPIC
Factors of 45: Prime Factorization, Methods, Tree, and Examples
Factors, an important category of statistical analysis, focus on breaking down a number (m) into a set of numbers that are capable of completely dividing m, without leaving any remainder behind. In simple words, factors of a given number are the set of numbers that when divided by the number, result in a whole-number quotient, and give zero as the remainder.For example,
Figure 1 – All possible Factors of 45
What Are the Factors of 45?
The factors of 45 are the follows: 1, 3, 5, 9, 15, and 45. Given that, these are the numbers, when multiplied in pairs, resulting in 45 as the product of their multiplication. The number 45 is a composite number by nature and has factors other than just a universal factor, i.e. 1 and itself. We can also say that the total number of factors of number 45 is 6, as stated above.How To Calculate the Factors of 45?
You can calculate the factors of a given number (m) simply by using the commonly used multiplication or division methods as one of the primary techniques.Here, as we are just focusing on finding the factors of 45, we will employ both the above-mentioned methods one at a time to construct a well-recognized list of the desired factors of 45. To begin with, we will multiply different pairs of numbers to achieve the required result, of 45. In this way, the group of numbers that lead us to 45 as their product will be referred to as factors of the number 45.1 x 45 = 45
Similarly,3 x 15 = 45
5 x 9 = 45
Hence, Factors of 45 = 1, 3, 5, 9, 15, 45 Now, we are going to find the set of factors of 45 by using the division method.The division approach states that the recommended number (e.g. 1, 2, 3, 4, 5, 6,……, n) is to be considered a factor of 45 if it is divided by 45 and the division leaves no or zero remainders behind. The procedures listed below should be used to calculate the factors of 45.At first, we are going to divide the given number i.e. 45 by the smallest recommended number i.e. 1. Check for the remainder. Is the remainder zero?\[ \dfrac {45}{1} = 45, r=0 \]Yes, the remainder is zero. Hence, we can say that the number 1 is a factor of 45. Similarly, we are going to divide 45 by the number 2 such that,\[ \dfrac {45}{2} = 22.5, r≠0 \]No, the remainder is not equal to zero. Additionally, the division failed to yield a quotient of whole numbers.Therefore, we can say that the number 2 is not a factor of 45. Keep on dividing 45 by the other set of numbers using the same method, as described previously. \[ \dfrac {45}{3} = 15 \]\[ \dfrac {45}{5} = 9 \]Hence,Factors of 45 = 1, 3, 5, 9, 15, 45 Each number has both positive and negative factors, as was already explained. Such that, the negative factors of the number are the additive inverse of its positive factors. The following is the list of the negative factors of 45.Negative Factors of 45 = -1, -3, -5, -9, -15, -45 Similarly, the following is the list of the positive factors of 45.Positive Factors of 45 = 1, 3, 5, 9, 15, 45Factors of 45 by Prime Factorization
Prime factorization is the most widely used technique to find the prime numbers that when multiplied together, result in producing a whole number. The numbers that pair together to carry out the multiplication are termed the prime factors. Therefore, prime factorization is another method used to find the factors of any given number. Now, to find the prime factors of a given number, a primary technique i.e. the prime factorization technique is used by following the unique upside down-division methodology commonly known as the ladder method. The prime factorization of the number 45 is given as follows,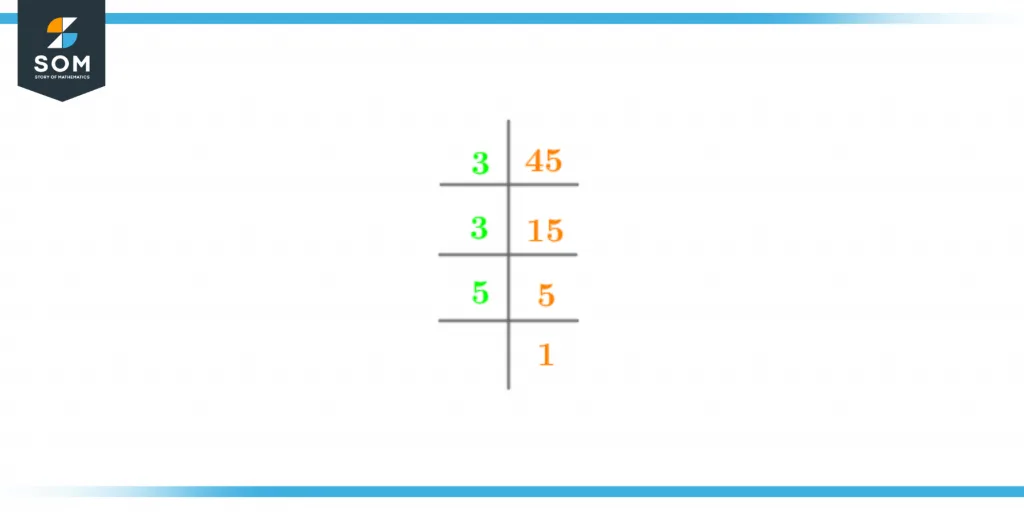
Figure 2 – Prime Factorization of 45
3 x 3 x 5 = 45
Hence, there are 3 prime factors of 45. Prime Factors of 45 = 3, 3, 5Factor Tree of 45
A factor tree is the graphic representation of the prime factors of a number. In the case of 45, the prime numbers 3, 3, and 5 are considered to be its prime factors. Such that, the following image shows the factor tree of the number 45,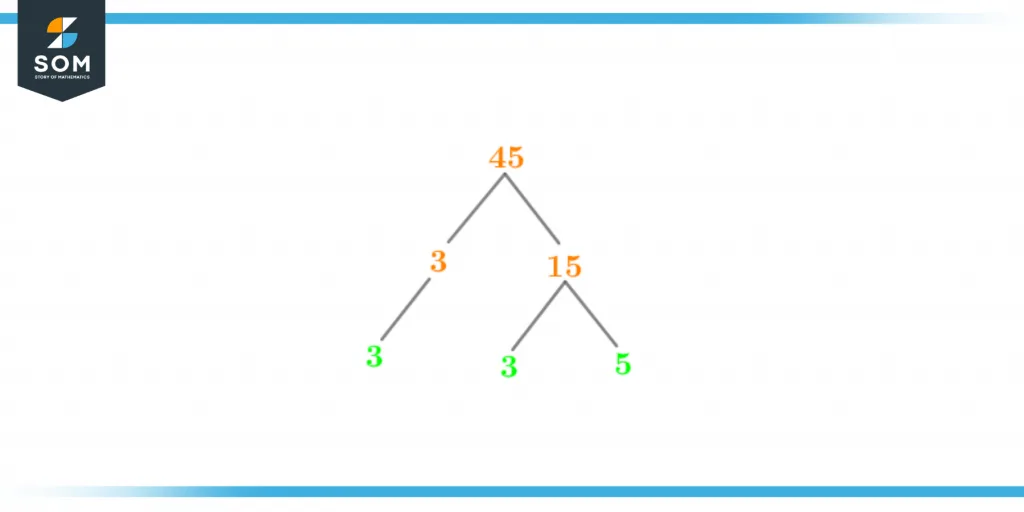
Figure 3 – Factor Tree of 45
- The sum of the factors of 45 is (1+3+5+9+15+45) = 78.
- The factors of 45 are odd, mainly due to the odd nature of 45.
- Apart from the number 45 itself, the two composite numbers that are factors of 45 are 9 and 15, which are themselves the product of two prime numbers. Such that:
3 x 3 = 9
3 x 5 = 15
Factors of 45 in Pairs
The pairs of factors are those sets that consist of numbers that when multiplied by one another give the same number as the product of which they are a factor. The factors of 45 are going to be called the pair factors when they are going to give the number 45 as the product of their multiplication. Luckily, the number 45 has 3 pairs of factors. The pair of factors of the number 45 are represented as,1 x 45 = 45
Where, (1, 45) is a factor pair of 45.Similarly,3 x 15 = 45
5 x 9 = 45
Hence, (3, 15), and (5, 9) are the remaining factor pairs of 45.The pair of factors can be both a set of negative or positive integers. Hence, the positive factor pairs of the number 45 are given as, Positive Factor Pairs of 45 = (1, 45), (3, 15), (5, 9) Also, the negative factor pairs of 45 are given as,Negative Factor Pairs of 45 = (-1,-45), (-3, -15), (-5,-9)