JUMP TO TOPIC
Factors of 46: Prime Factorization, Methods, Tree, and Examples
Factors of 46 are the whole numbers that divide 46 without leaving any remainder. A number has positive as well as negative factors.
Figure 1 – All possible Factors of 46
What Are the Factors of 46?
Factors of 46 are 1, 2, 23, and 46. All of these integers can divide 46 evenly. That means the remainder is zero.46 is an even composite number. A number having more than two factors is known as a composite number.How To Calculate the Factors of 46?
You can calculate the factors of 46 by two methods: Division method and Multiplication method. We will discuss both ways in this article.The number 46 is composite, so there must be more than two factors of 46. The factors of a number can never be greater than the number itself. Factors of 46 by division method:When we divide 46 by a number and the remainder is zero, that number will be the factor of 46. Not only that, but the number quotient will also be a factor of 46.The number 1 is a factor of every number because every number is evenly divided by 1.\[ \frac{46}{1} = 46 \]\[ \frac{46}{-1} = -46 \]The number 1 and -1 are specific factors of 46.46 is even so that it will be divided by 2.\[ \frac{46}{2} = 23 \]\[ \frac{46}{-2} = -23 \]The numbers 2 and -2 are factors of 46.Now divide 46 by 3:\[ \frac{46}{3} = 15.33 \]When we divide 46 by 3, the number is not evenly divided. 3 is not a factor of 46.\[ \frac{46}{23} = 2 \]\[ \frac{46}{-23} = -2 \]Hence, proving the statement is correct, 23 and -23 are also the factors of 46.Every whole number is a factor in itself. Every number divides itself evenly, and the remainder is always zero. 46 and -46 are also the factors of 46.Positive factors of 46 = 1, 2, 23, 46. Negative factors of 46 = -1, -2, -23, -46. Factors of 46 by multiplication method:For multiplication, the method keeps the law of multiplication in mind. This says that when two positive numbers are multiplied, the product is always positive; when a positive number is multiplied by a negative number, the product is always negative, and when a negative number is multiplied by a negative number, the result is always positive.1 x 46 = 46
2 x 23 = 46
-1 x -46 = 46
-2 x -23 = 46
Factors of 46 are 1, -1, 2, -2, 23, -23, 46, and -46.Number 46 has eight factors in total, four positive factors and four negative factors.Interesting facts:- 46 is the largest even integer that can’t be written as the sum of two abundant numbers.
- Factors can never be in the form of fractions or decimal forms.
- A factor can never be bigger than the number itself.
- The number 1 is a factor of every number.
- Prime numbers have only two factors, one and number itself.
- Composite numbers have more than two factors.
Factors of 46 by Prime Factorization
Prime Factorization is a mathematical technique that expresses the number 46 as the product of its prime factors only. Prime factorization is done by dividing 46 by its prime factors only. First of all, list down the prime factors of 46.Prime factors of 46: 2 and 23.Prime factors are the prime numbers. One is not a prime number.Divide 46 by the smallest prime factor, which is 2.\[ \frac{46}{2} = 23 \]23 is not divisible by 2. Divide the quotient by 23.\[ \frac{23}{23} = 1 \]The Prime Factorization of 46 is shown below in figure 1: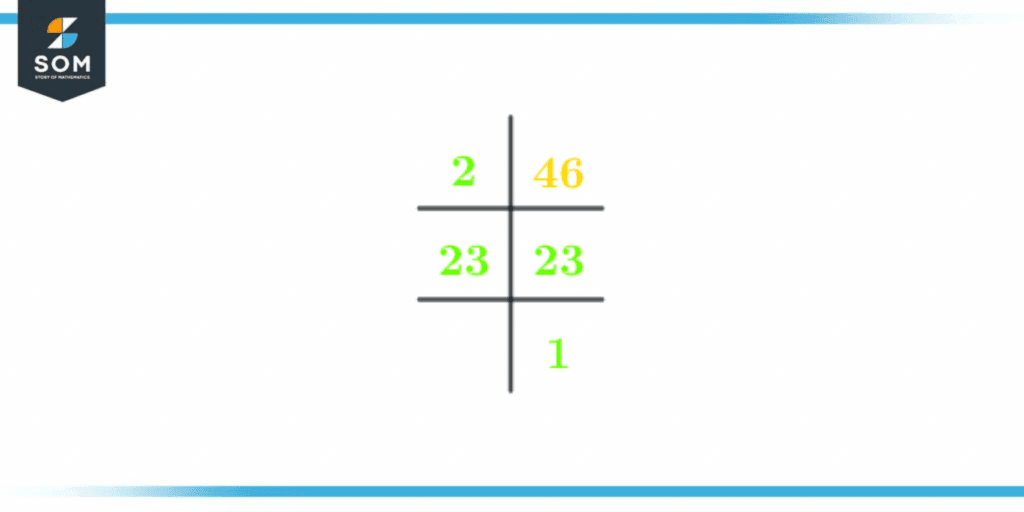
Figure 2 – Prime Factorization of 46
Factor Tree of 46
The factor tree is a diagram representing a number’s factors, specifically the prime factors. The number 1 is not prime, so it will never appear in any factor tree.A factor tree is used to find a number’s highest common factor and the least common factor. It also helps us to identify whether the number is a cube, square, or prime.- Write the given number at the top of the tree.
- Split it into two branches.
- Top up these branches with the factors of the given number.
- Carry on dividing until each branch consists of prime factors.
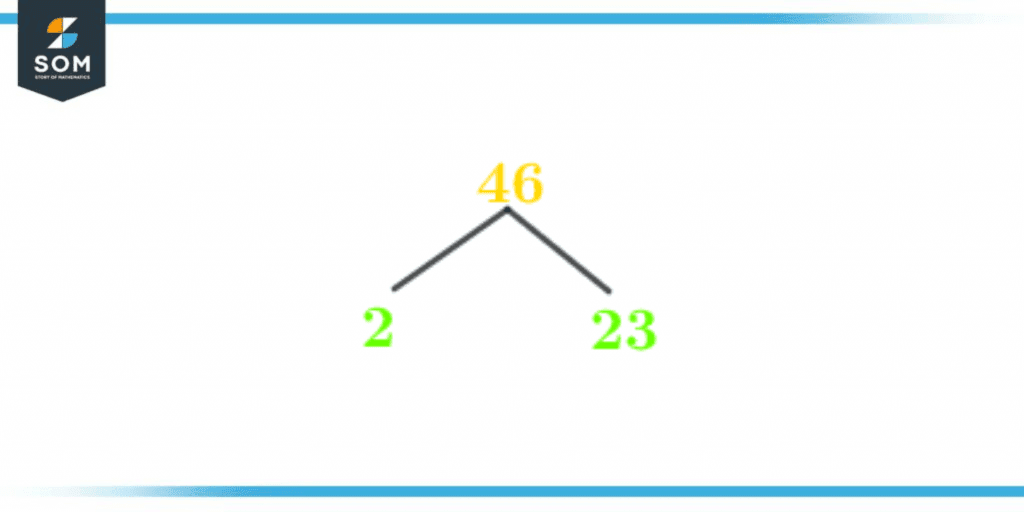
Figure 3 – Factor Tree of 46
Prime Factorization of 46 = 2 x 23
Factors of 46 in Pairs
Factor pairs are the whole numbers from a given number’s list of factors that result in the given number once multiplied. Factor pairs can be identified by multiplication. Multiply the factors with each other to obtain the perfect factor pairs.You can also identify the factor pairs by division. When the quotient and the divisor are multiplied, it will result in the number 46.(1, 46)
(2, 23)
The same goes for the negative factors of a number. Negative factors differ by a negative sign.(-1, -46)
(-2, -23)
Factors of 46 Solved Examples
Here are some solved examples for a better understanding regarding factors of 46.Example 1
Help Anna find the sum S1 of all composite factors of 46 and divide it by the sum S2 of all prime factors of 46.Solution
The factors list of 46 is 1, 2, 23, and 46.Composite numbers are the numbers that have more than two factors. One is not a prime number nor a composite number.Composite factors of 46: 46 is the only composite factor in itself. Sum S1: 46A prime number has only two factors the number one and itself.Prime factors of 46: 2,23 Sum S2: 2 + 23 = 25The given statement says that dived S1 by S2.\[ \frac{46}{25} = 1.84 \]The answer is: 1.84Example 2
Jony wants to plant 46 sunflower plants, 80 rose flower plants, and 50 jasmine flower plants in his garden. If he puts the same number of plants in each row and each row has only one type of flower plant, what is the greatest number of flower plants Jony can put in one row?Solution
Jony has 46 sunflower plants, 80 rose flower plants, and 50 jasmine flower plants.First, find the factors of 46, 50, and 80.A factors list of 46 is given below:Factors of 46 = 1, 2, 23, 46
A factors list of 50 is given below:Factor list of 50 = 1, 2, 5, 10, 25, 50
A factors list of 80 is given below:Factors of 80 are the following: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Now find the greatest common factor among them.Greatest Common Factor (GCF) is the largest factor that is common in all factors lists.GCF of 46, 50, and 80 = 2
Jony can place two flower plants in one row.