JUMP TO TOPIC
Factors of 512: Prime Factorization, Methods, Tree, and Examples
Factors of 512 are the numbers that completely divide 512, leaving zero as the remainder behind. In other terms, these are the numbers upon which 512 is completely divisible.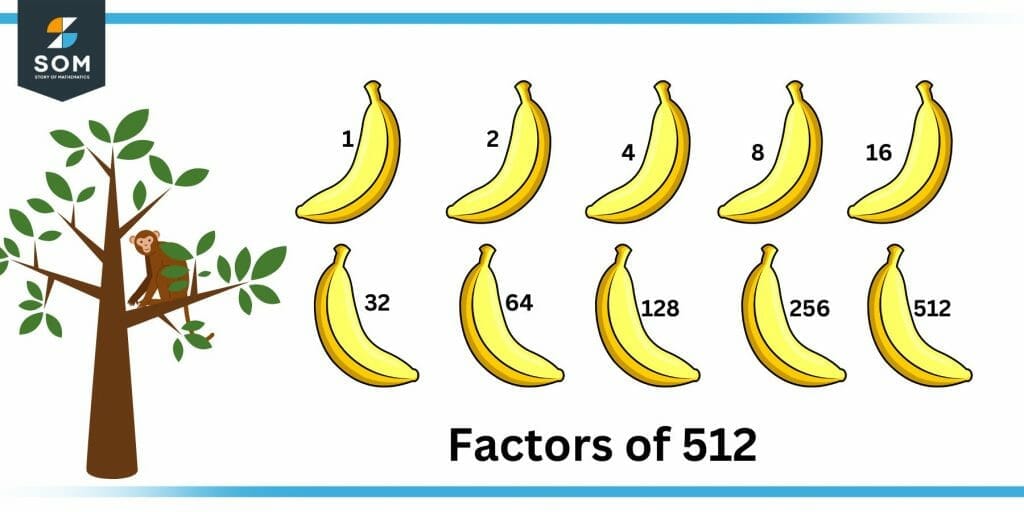
Figure 1 – All possible factors of 512
2 x 256 = 512
In this article, we will dive into the factors of 512. We will take a comprehensive look at these factors and will discover the various methods to determine these factors.What are the Factors of 512?
The factors of 512 are 1, 2, 4, 8, 16, 32, 64, 128, 256, and 512. These factors can also be paired into factor pairs by pairing the numbers which yield 512 as the product.In total, the number 512 has 10 factors. When the number 512 is divided by these factors, the remainder is always zero.How To Calculate the Factors of 512?
You can calculate the factors of 512 by making use of the technique mentioned above. Since half of 512 is 256, we will check for the divisibility of 512 from numbers starting from 1 to 256. The divisors that yield zero as the remainder are considered to be factors of 512. These divisors only produce whole number quotients. For understanding this concept, let’s consider the division of 512 from two numbers; 2 and 3.\[ \frac{512}{2} = 256 \]\[ \frac{512}{3} = 170.667 \]Since a whole number quotient is obtained only from the division of 512 from 2, hence 2 is the factor.We also mentioned above that the divisors which produce zero as the remainder form factor pairs with their quotients. This means that the quotients of such divisors are also factors. Hence 256 is also a factor of 512.All the possible divisions of 512 are mentioned below:\[ \frac{512}{1} = 512 \]\[ \frac{512}{2} = 256 \]\[ \frac{512}{4} = 128 \]\[ \frac{512}{8} = 64\]\[ \frac{512}{16} = 32 \]All these divisions produce zero as the remainder so possible factors of 512 are:Factors of 512 = 1,2,4,8,16,32,64,128,256, 512
Factors of 512 by Prime Factorization
Prime Factorization is the method of determining which prime factors can multiply with each other to give the number as the product. In other words, it is defined as the method of multiplying prime numbers to obtain the said number as the product. So Prime Factorization is the process in which the breakdown of the quotient keeps on occurring until 1 is received as the end quotient. For the given number, 512, the possible prime number which you can choose to divide 512 is 2. So the division is given below:\[ \frac{512}{2} = 256 \]Now, we will continue the division process until we receive 1 at the end. \[ \frac{256}{2} = 128 \]\[ \frac{128}{2} = 64 \]\[ \frac{64}{2} = 32 \]\[ \frac{32}{2} = 16 \]\[ \frac{16}{2} = 8 \]\[ \frac{8}{2} = 4 \]\[ \frac{4}{2} = 2\]\[ \frac{2}{2} = 1 \]Therefore, the prime factor of 512 is 2. The prime factorization of 512 is also shown below: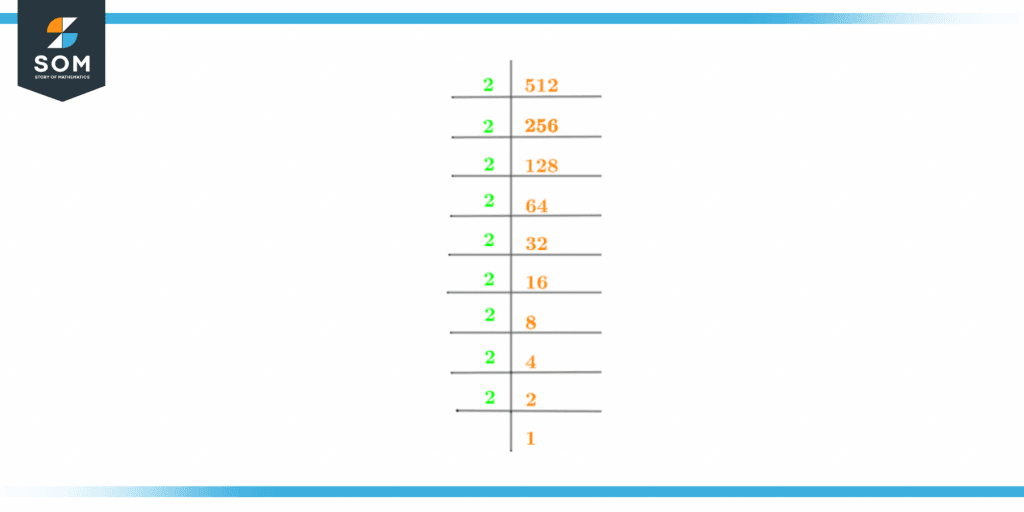
figure 2 – Prime Factorization of 512
Factor Tree of 512
There are more than one ways to represent the factors of a specific number and the Factor Tree is one of them. The Factor Tree of any number is the visual representation of the prime factors of that number.The Factor Tree begins with the number itself and extends out till a prime number is received at the end. According to the prime factorization, 2 is the prime factor of the number 512 so the Factor Tree must also yield 2 as its last branch. The Factor Tree of 512 is shown below: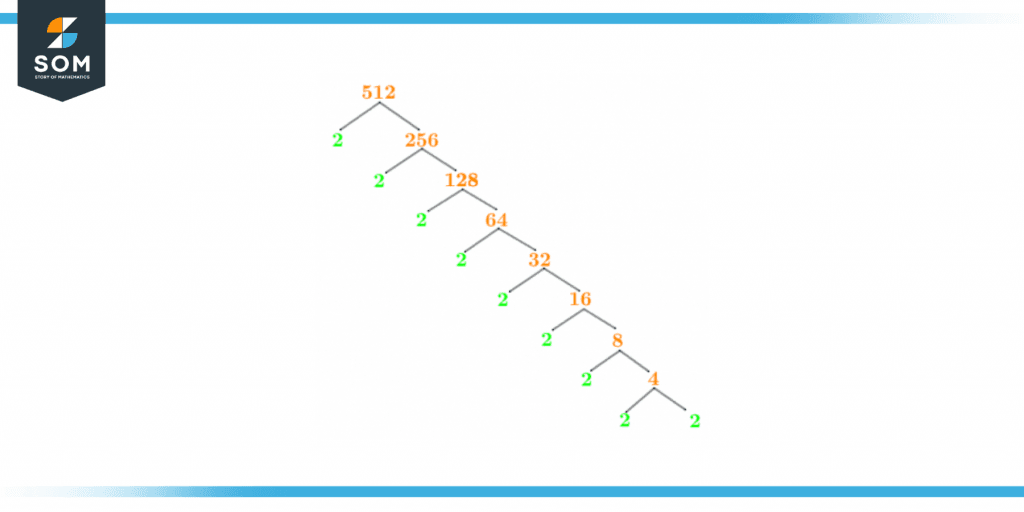
Figure 3 – Factor Tree of %12
Factors of 512 in Pairs
The Factor Pairs are the pair of numbers when multiplied together produce the number itself. In this case, it refers to the two numbers, which when multiplied, will produce 512. The factor pairs of 512 can be found as follows:1 x 512 = 512
2 x 256 = 512
4 x 128 = 512
8 x 64 = 512
16 x 32 = 512
So the factor pairs are:Factor Pairs = (1,512), (2, 256), (4, 128), (8,64), (16, 32) The negative factors are just as same as the positive factors. The only difference is that the signs are reversed. For instance, the negative factor pairs of 512 are given below:Factor Pairs = (-1,-512), (-2, -256), (-4, -128), (-8,-64), (-16, -32)Factors of 512 Solved Examples
To further enhance the concept of factors of 512, given below are a few examples.Example 1
Calculate the average of the factors of 512.Solution
The factors of 512 are given below:Factors of 512 = 1,2,4,8,16,32,64,128,256, 512 The average of these factors is determined by calculating the sum of these factors and dividing it by the total number of factors.So the average is given by:\[ Average = \frac{\text{Sum of factors}}{\text{Total number of factors}} \]\[ Average = \frac{1+2+4+8+16+32+64+128+256+512}{10} \]\[ Average = \frac{1023}{10} \]Average = 102.3
