JUMP TO TOPIC
Factors of 52: Prime Factorization, Methods, Tree, And Examples
The Factors of 52 are the numbers upon which the number 52 is entirely divisible, meaning that when such numbers act as the divisors for 52, they leave zero as the remainder behind.

Figure 1 – All possible Factors of 52
The factors of 52 can also be recognized as those numbers that produce 52 as the product when these numbers are multiplied by each other. Together these two numbers formulate a factor pair.
The number 52 is even composite. Since the number 52 is composite, so this automatically means that 52 will have more than 2 factors. 52 is also an even number which indicates that one of the factors of 52 will be 2.
The factors of 52 can be primarily determined through two main methods – the division method and the prime factorization method. The factors of 52 can also be categorized into prime factors and these prime factors can be pictorially presented via a factor tree.
In this article, we will take a detailed look at the two methods for determining the factors of 52. We will also construct a factor tree for 52 and will go through some examples constituting the factors of 52.
What Are the Factors of 52?
The factors of 52 are 1, 2, 4, 13, 26, and 52. All these yield zero as the remainder and a whole number quotient when they act as the divisors for the number 52.
In total, the set of factors of 52 consists of 6 numbers. These factors can be negative as well. These factors can also be split into factor pairs.
How To Calculate the Factors of 52?
You can calculate the factors of 52 through various techniques, one of which is the division method. Let’s first take a look at this most common technique.
Division
Before moving on to determining the factors of 52, it is necessary to first find out the range in which these factors lie since an infinite number of possibilities exist. An easy way to find the range of the factors is to look for numbers lying between the smallest factor 1 and the half of that number.
Since the half of 52 is 26, so to determine the factors of 52, apply the division method to all the possible numbers existing between 1 and 26.
Moreover, in the factors of 52, the number 1 acts as the smallest factor, and the number itself, in this case, 52, acts as the largest factor. Now let’s move on to the division method.
The condition for a number to be qualified as a factor is that it should produce zero as the remainder and a whole number quotient when it acts as the dividend. Since 52 is an even number, so let’s first look at the division of 52 with 2.
\[ \frac{52}{2} = 26 \]
As a whole number quotient is produced, hence the number 2 qualifies as a factor of 52. Additional factors of 52 are given below:
\[ \frac{52}{1} = 52 \]
\[ \frac{52}{4} = 13 \]
\[ \frac{52}{13} = 4 \]
\[ \frac{52}{26} = 2\]
\[ \frac{52}{52} = 1 \]
The list of all the factors of 52 is given below:
Factors of 52: 1, 2, 4, 13, 26, 52
These factors can be negative as well. Negative factors are the same as positive factors the only difference is the negative sign. So the list of negative factors is given below:
Negative Factors of 52: -1, -2, -4, -13, -26, -52
Factors of 52 by Prime Factorization
The prime factorization technique is another method for determining the factors of a number to be more precise, the prime factorization technique is used to determine the prime factors for a number.
The factors for any number include both prime as well as composite numbers. Prime factors refer to only those factors which are the prime numbers. These prime factors can be discovered through the prime factorization method.
In prime factorization, the division process is continued with the help of only prime numbers. The quotient obtained as the result of the first division then acts as the dividend in the next division step. This division continues till 1 is achieved at the end. The prime factorization of 52 is shown below:
52 $\div$ 2 = 26
26 $\div$ 2 = 13
13 $\div$ 13 = 1
So the prime factorization of 52 can be mathematically written as follows:
Prime Factorization of 52 = 2 x 2 x 13
OR
Prime Factorization of 52 = $2^{2}$ x 13
The prime factorization of 52 is also shown below in figure 1:
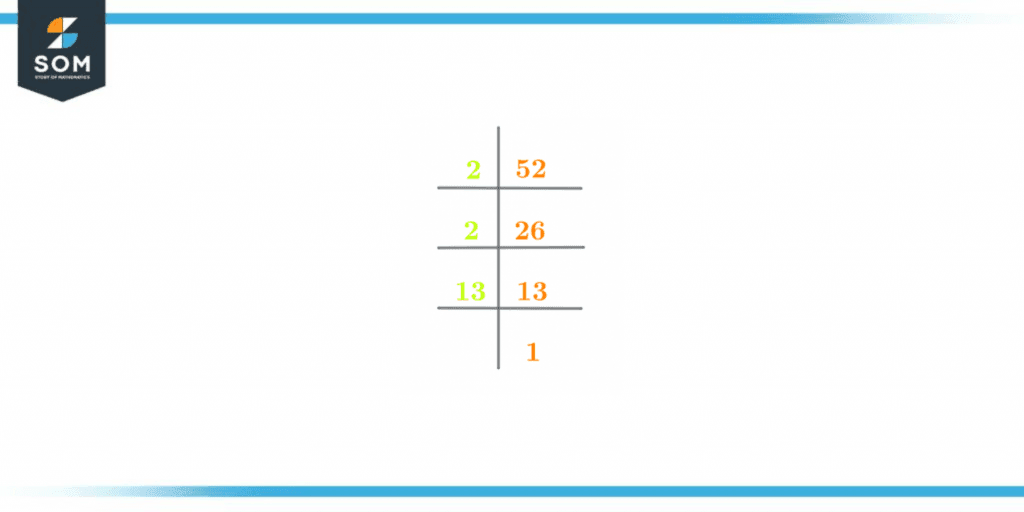
Figure 2 – Prime Factorization of 52
According to this prime factorization, the following prime factors are obtained:
Prime Factors = 2, 13
Factor Tree of 52
The factor tree is a pictorial description of the prime factorization technique. The factor tree is also used to determine the prime factors.
Since the factor tree is a visual representation of the prime factorization so the division process is carried out in the same way as in prime factorization. The only difference is that instead of ending at 1, the factor tree terminates at prime numbers.
The factor tree for the number 52 is shown below:
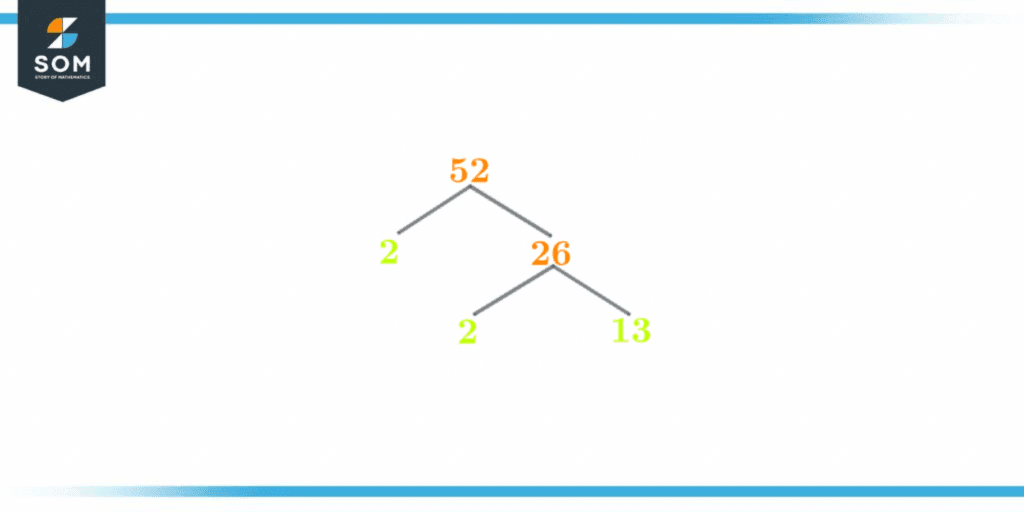
Figure 3 – Factor Tree of 52
Factors of 52 in Pairs
The factors of 52 can also exist in the form of a factor pair. A factor pair consists of a pair of numbers that produce the original number when they are multiplied together. 2 numbers only can exist within a pair.
An easy way to find the factor pairs is through the division method. When a factor acts as the divisor for the number, it produces a whole number quotient. This divisor can then form a factor pair with the whole number quotient.
To understand this statement, consider the division given below:
\[ \frac{52}{2} = 26 \]
When 2 acts as the divisor, 26 is produced as a whole number quotient. Hence, 2 can form a factor pair with 26 which is evident from the multiplication shown below:
2 x 26 = 52
Since the number 52 consists of 6 factors in total, so these 6 factors can be divided into three-factor pairs. These factor pairs are given below:
1 x 52 = 52
2 x 26 = 52
4 x 13 = 52
Hence the factor pairs of 52 are given below:
Factor Pairs of 52 = (1, 52), (2, 26), and (4, 13)
These factor pairs can be negative as well. The condition for negative factor pairs is that both the numbers existing within a pair need to have a negative sign so they can yield a positive product when they are multiplied together. The negative factor pairs for 52 are given below:
-1 x -52 = 52
-2 x -26 = 52
-4 x -13 = 52
Negative Factor Pairs of 52 = (-1, -52), (-2, -26), and (-4, -13)
Factors of 52 Solved Examples
To further comprehend your understanding of the factors of 52, given below are a few examples constituting the factors of 52.
Example 1
Determine the sum of all the factors of 52 and figure out whether the result is divisible by 2 or by 3.
Solution
To determine the sum of all the factors 52, let’s first list these factors. The factors of 52, are given below:
Factors of 52 = 1, 2, 4, 13, 26, 52
The sum of the factor of 52 is given below:
Sum of factors of 52 = 1 + 2 + 4 + 13 + 26 + 52
Sum of factors of 52 = 98
The resultant number obtained as a result of adding all the factors of 52 is 98.
Since the number 98 is an even number so it is obvious that the number is a multiple of 2.
2 x 49 = 98
This indicates that the number 98 is a multiple of 2.
To determine if 98 is a multiple of 3, simply add the digits and determine if the resulting number is a multiple of 3.
The sum of the digits of 98 is: 9 + 8 = 17
Since 17 is not a multiple of 3, hence the number 98 is also not a multiple of 3.
Example 2
Find the difference between the product of the even factors of 52 and the product of the odd factors of 52.
Solution
To proceed with the solution, let’s first note the factors of 52:
Factors of 52 = 1, 2, 4, 13, 26, 52
Now, let’s determine the even factors of 52.
Even factors of 52 = 2, 4, 26, 52
The product of even factors of 52 is given below:
Product of even factors = 2 x 4 x 26 x 52
Product of even factors = 10816
Now, let’s move on to the odd factors. The odd factors of 52 are given below:
Odd factors of 52 = 1, 13
Product of odd factors of 52 = 1 x 13
Product of odd factors of 52 = 13
Now, calculating the difference in the product of the even factors and the odd factors of 52:
Difference = Product of even factors – Product of odd factors
Difference = 10816 – 13
Difference = 10803
So the difference in the products of even and odd factors of 52 is 10803.
All images/mathematical drawings are created with GeoGebra.
