JUMP TO TOPIC
Factors of 55: Prime Factorization, Methods, Tree, and Examples
Factors of 55 refer to the numbers that, when multiplied together, equal 55 or are the numbers by which 55 can be wholly divided. As a result, an integer is considered a factor if it divides 55 with a remainder of 0.

Figure 1 – All possible Factors of 55
Write down all the integers that are less than or equal to the number you are looking for to see whether it has any factors. Then, use this list to check for factors of the number.
For example, the number 55 will range from 1 to 11. To find the solution, divide each of them. It’s interesting to note that the factor of all integers is two.
Moreover, the factors of a number can be found using division and multiplication. Yet, there are several methods for discovering integer factors. Finding a number’s factors can be done in more straightforward ways.
The quotient and divisor are regarded as factors of the supplied number once the remainder equals zero, which can be determined by simply dividing the number by itself until the remainder equals zero.
Let’s use one of these situations as an example. The outcome of 55 divided by 5 is 11. That being said, both the solution and the divisor are classified as factors. As a pair, they are known as factor pairs, i.e. (5, 11).
For a better understanding, this page will do its best to provide all the information relating to factors of 55. Simple solutions, excellent explanations, and intriguing details about the number 55 are all included.
What Are the Factors of 55?
The factors of 55 are 1, 5, 11, and 55.
Since 55 is a composite number, it includes more than two factors. The factors of 55 are the values that divide the number 55 precisely without leaving a remainder.
All in all, there are four factors of 55. The pair factors of 55 are the numbers multiplied by each other in pairs to get the number 55, such as (1, 55) and (5, 11).
How To Calculate the Factors of 55?
To calculate the factors of 55, the easiest and most effective method to use would be the division method. Remember that a number must be divisible by a number that yields a whole number quotient and that the remainder must have zero value to be a factor of 55.
Division
If the number gives a decimal number, that result will also not be considered.
The basic division method to find out the factors of 55 is given below:
The smallest divisor you can find to divide 55 by is 1. Given this, one is one of the factors of 55.
\[ \frac{55}{1} = 55 \]
The following whole number is then tested to see if it can successfully split 55 in half.
\[ \frac{55}{2} = 27.5 \]
This shows that 2 is not a factor of 55.
We can stop dividing by whole numbers once we reach \[ \frac{55}{55} = 1 \]. We are therefore unable to use any more whole numbers.
Following are the factors of 55 through the division method:
\[ \frac{55}{1} = 55 \]
\[ \frac{55}{5} = 11 \]
\[ \frac{55}{11} = 5 \]
\[ \frac{55}{55} = 1 \]
Therefore, all the factors of 55 are 1, 5, 11, and 55.
Let’s now focus on finding the factors through multiplication. Consider 55 the outcome of two whole integers in all feasible configurations. Every integer in each of these products is one of the factors of 55.
For example:
1 x 55 = 55
5 x 11 = 55
Hence, stated above are the factors of 55.
Factors of 55 by Prime Factorization
One way to express a specific number as the product of its prime factors is to use the Prime factorization method, which involves determining which prime factors can multiply with one another to get the number as a product.
In other words, it is a method for determining or showing a given integer as the sum of prime integers. There are only two factors to a prime number: one and the number itself.
As 55 is a composite number, it should contain prime factors. Let’s learn how to identify the critical factors of 55. First, divide 55 by the smallest prime factor; for this example, let’s pick 2.
55 divided by two will provide a fractional number when split; thus, we may move on to the following prime number 3. 3 is also not a factor of 55, as shown below.
\[ \frac{55}{2} = 27.5 \]
\[ \frac{55}{3} = 18.3 \]
We continue with the following numbers and ultimately find out the prime factors of 55.
\[ \frac{55}{5} = 11 \]
Following the dividing process, the number 1 was assigned to us. Because of it, we finally cannot continue. To denote the prime factors of 55, the notation 5 x 11 is used. Prime numbers are 5 and 11 in this case.
Now let’s take a look at the diagram of the prime factorization of 55:
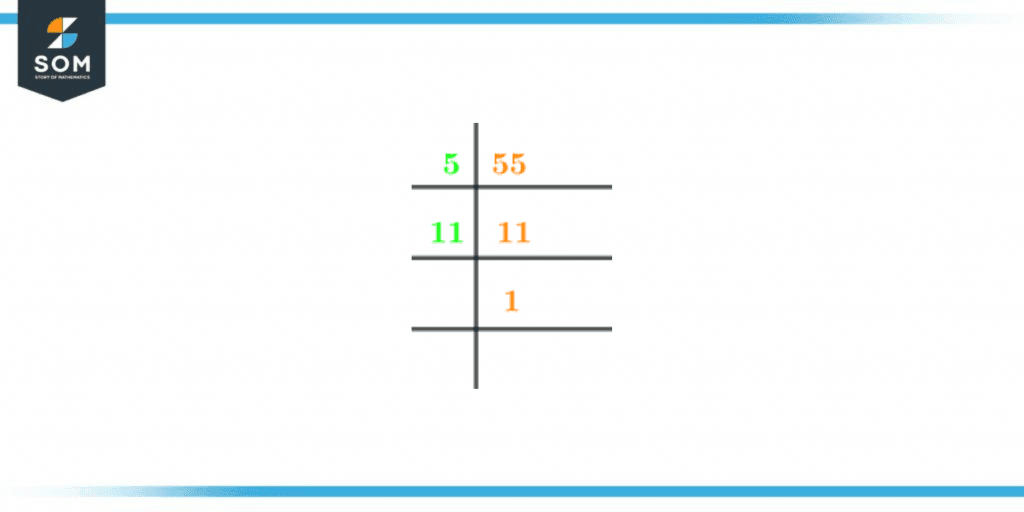
Figure 2 – Prime Factorization of 55
Factor Tree of 55
There are several ways to graphically portray a number’s prime factors, one of which is to display characteristics as a Factor Tree. The actual number serves as the root of the factor tree, and the branches that emerge from it represent factors until you get the prime number.
Therefore, 5 and 11 are the prime factors of 55 as determined by prime factorization.
Let’s take a look at the diagram of the Factor tree of 55:
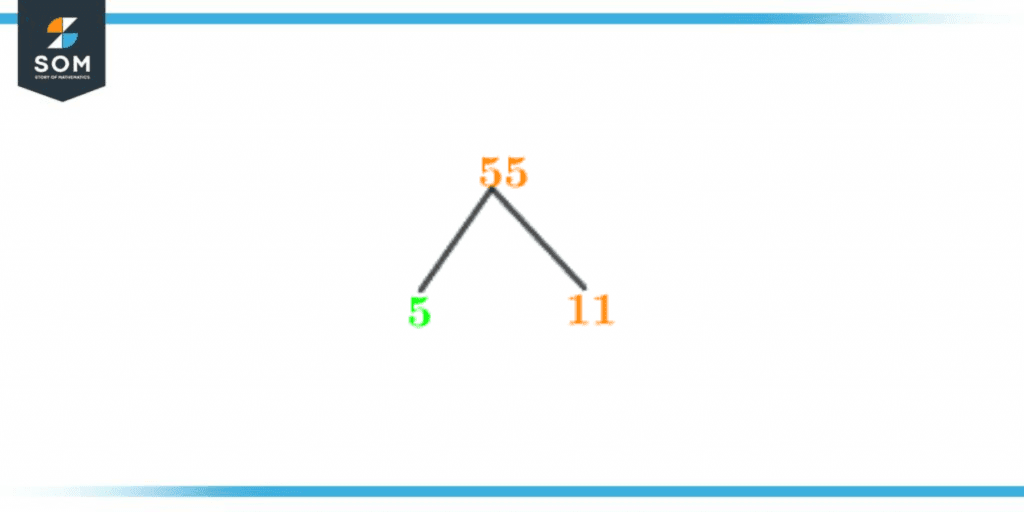
Figure 3 – Factor Tree of 55
Super-fun facts about the number 55 are as follows:
- 55 is a heptagonal number, a centered nonagonal number, a square pyramidal number, and the sum of the squares of the integers 1 – 5.
- The tenth Fibonacci number is 55. Also, 55 is a doubly triangular number and a Kaprekar number in base 10.
- 55 is the atomic number of Cesium
- From 1974 until 1987, the National Maximum Speed Law in the US outlawed speed restrictions greater than 55 mph, i.e., 90 km/h.
- The Albanian newspaper’s name is Gazeta 55. Additionally, a regulation from the Communist era of Albania known as Constitution Law 55 prohibits agitation and propaganda against the state.
- ‘’55’’ and ‘’I Can’t Drive 55’’ are songs by Mac Miller and Sammy Hagar, respectively.
- 55 is Brazil’s country code for International direct dial calls.
- A film featuring Charlton Hesston and David Niven is called 55 Days at Peking. Furthermore, an American band is known as Primer 55.
Factors of 55 in Pairs
Factors of 50 are two numbers multiplied together until they equal 50. Here are the factor pairs:
If 1 × 55 = 55, then (1, 55) is a pair factor of 55. Let’s look at all the pairs:
1 x 55 = 55, (1, 55) is a pair factor of 55.
5 x 11 = 55, (5, 11) is a pair factor of 55.
11 x 5 = 55, (11, 5) is a pair factor of 55.
55 x 1 = 55, (55, 1) is a pair factor of 55.
A list of the positive factor pairs is given above. The negative factor pair can be identified by simply swapping the signs. The list that follows includes 55’s negative pair factors:
-1 x -55 = 55, (-1, -55) is a pair factor of 55.
-5 x -11 = 55, (-5, -11) is a pair factor of 55.
-11 x -5 = 55, (-11, -5) is a pair factor of 55.
-55 x -1 = 55, (-55, -1) is a pair factor of 55.
Factors of 55 Solved Examples
Example 1
What are the common factors between the numbers 55 and 60?
Solution
The Factors of 55 are as follows:
1, 5, 11, and 55.
There are six factors that make up 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60.
Thus, the common factors between 55 and 60 are 1 and 5.
Example 2
Find the product of all the factors of 55.
Solution
Factors of 55 are as follows:
1, 5, 11, and 55.
1 x 11 x 55x 5 = 3,025
So the answer to this example is 3,025.
Example 3
To create the ideal learning environment, grade 9 teacher Molly wants to organize the class’s 55 desks into rows instead of groups.
She wants the same number of desks in each row. What a maximum number of rows could the classroom have based on this information?
Solution
The factors of 55 are already known to be 1, 5, 11, and 55. Each row may have either 5 or 11 desks because a row cannot contain either all of the desks or only one.
Thus, Molly will have to arrange the class by making 5 or 11 rows.
Example 4
Determine the sum of all the factors of 55.
Solution
Factors of 55 are given below:
1, 5, 11, and 55.
1 + 11 + 55 + 5 = 72.
Thus, the sum of all the factors of 55 is 72.
All the images/diagrams are created using GeoGebra.
