JUMP TO TOPIC
Factors of 56: Prime Factorization, Methods, Tree, and Examples
In the field of mathematics, factorization is the process of breaking a larger number into pairs of two smaller numbers. Factors of a number are termed as its divisors such that these are the set of positive and negative numbers that completely divide the given number.
Figure 1 – All possible Factors of 56
What Are the Factors of 56?
The factors of 56 are 1, 2, 4, 7, 8, 14, 28, and 56. The value 56 is the biggest factor of number 56.Given that, all the aforementioned numbers are the set of whole numbers that when present in pairs, resulting in producing 56 as their product. Since 56 is an even composite number, it has more factors besides simply itself and 1. In other words, the total number of factors of number 56 is 8, as stated above.How To Calculate the Factors of 56?
You can calculate the factors of 56 by determining the whole numbers that are completely divisible by 56. The division and multiplication procedures are the two primary methods used to determine the factors of any given integer.Here, in the current article, we are going to use both methods to compute the factors of 56. In the first step, we are going to use the simplest-division methodology to calculate the well-recognized list of factors 56. Initially, divide 56 with the smallest possible expected factor i.e. 1. Note, whether the answer of the division process is a whole-number quotient or not. If yes, then look for the remainder. Is the remainder of the desired division process zero?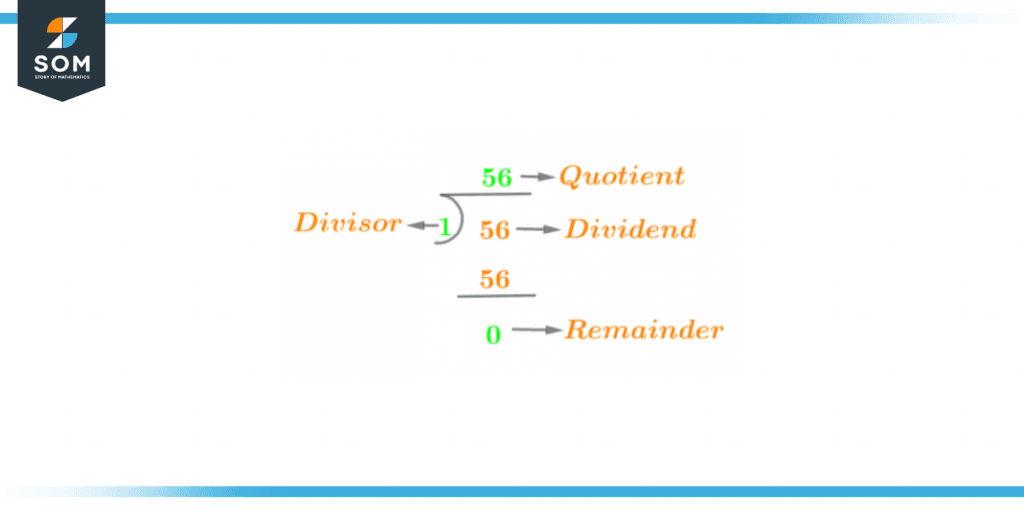
Figure 2 – Division Method of 56
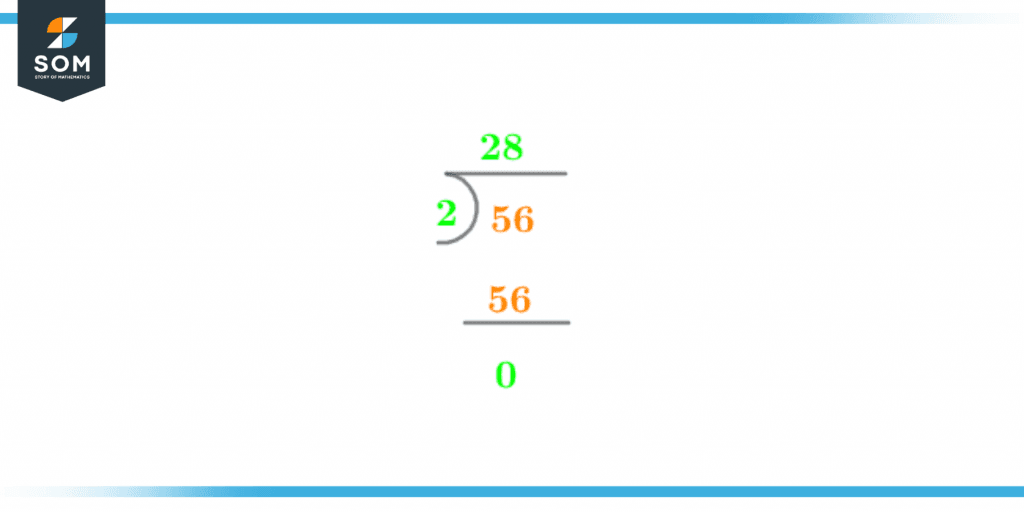
Figure 3 – Division Process of 56
1 x 56 = 56
Similarly, the further factors are given as:2 x 28 = 56
4 x 14 = 56
7 x 8 = 56
Hence, it has been seen that the numbers 1, 2, 4, 7, 8, 14, 28, and 56 are the factors of 56.Factors of 56 by Prime Factorization
Prime factorization is the process of splitting a number into its prime or distinct prime factors. Given that, the prime factors of a given number are a set of prime numbers that when multiplied together in pairs, resulting in the original number to which they are a factor. Besides, division and multiplication, prime factorization is also a widely used technique used to find the well-recognized factors of a number. Here, we are going to use the famous upside-down methodology to determine the factors of 56 by prime factorization. The following technique is also referred to as the ladder method since the division is shown visually in a ladder-like fashion.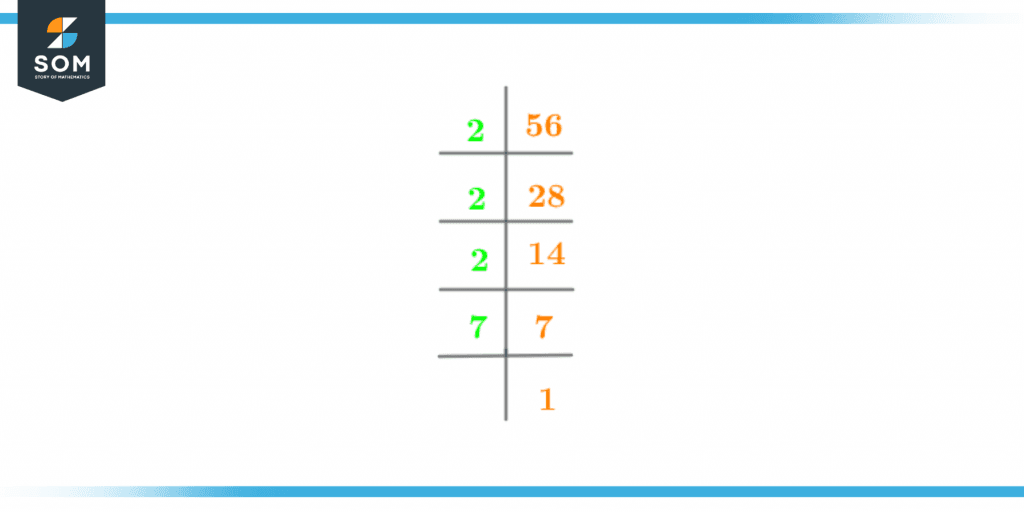
Figure 4 – Prime Factorization of 56
2 x 2 x 2 x 7 = 56
Hence, there are 4 prime factors of 56. Here are a few fun facts regarding the factors of 56,- The factors of 56, just like the factors of any other number, can never be fractions or decimals.
- The sum of the factors of 56 is given as follows,
(1+2+4+7+8+14+28+56) = 120
- The prime factors of 56 are also termed as the distinct prime factors such that there are only 2 distinct factors of the number 56.
Factor Tree of 56
A factor tree is a geometric portrayal of a number’s factors in which the prime factors are represented through its branches such that, these factors may be any number other than one. To ascertain a number’s nature, a factor tree is employed. It may foretell if a number is square, cubic, or prime. The factor tree may also be used to determine the L.C.M and H.C.F. The following image shows the factor tree of the number 56.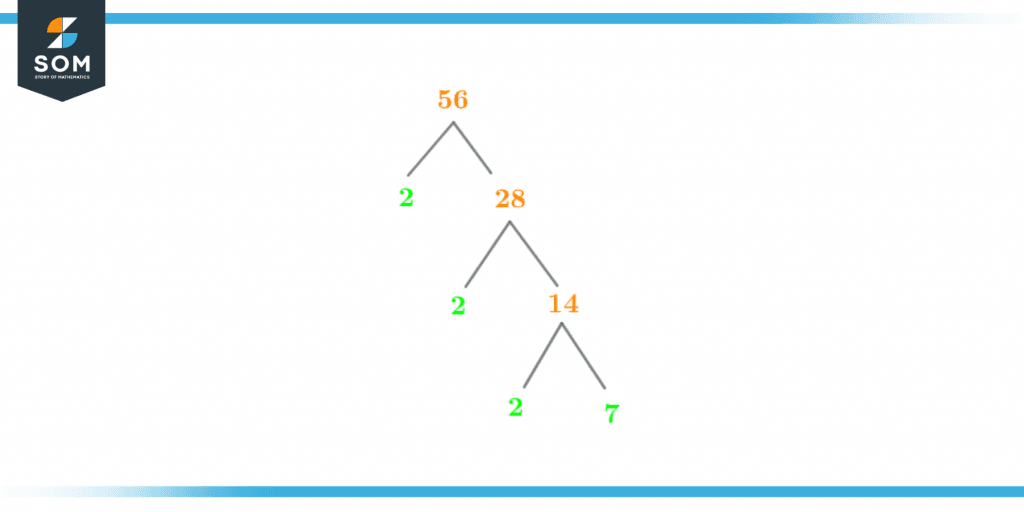
Figure 5 – Factor Tree of 56
Factors of 56 in Pairs
As was already mentioned above, when two factors of a given number (m) are multiplied in pairs, the outcome of the multiplication is the original number. Now, the question that arises here is what are these pairs termed as? The answer to the above question is pair of factors. Yes, the pairs that combine to produce the original number are referred to as the factor pairs or pairs of factors. The method used to get the factor pairs of 56 is the same one used to find the factor pairs of any other number. As a result, the pair of factors of the number 56 are shown as,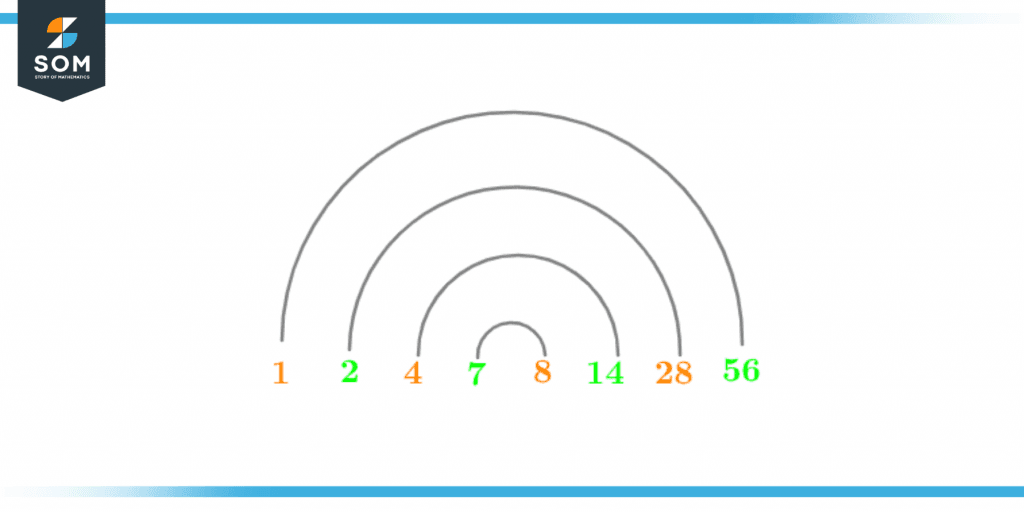
Figure 6 – Factor Pair of 56
1 x 56 = 56
2 x 28 = 56
4 x 14 = 56
7 x 8 = 56
Hence, the positive factor pairs of the number 56 are given as:Positive Factor Pairs of 56 = (1, 56), (2, 28), (4, 14), (7, 8) The pair of factors are described in terms of both the positive and negative integers. Therefore, the negative factor pairs of 56 are given as:Negative Factor Pairs of 56 = (-1,-56), (-2, -28), (-4, -14), (-7,-8)