JUMP TO TOPIC
Factors of 58: Prime Factorization, Methods, Tree, and Examples
The factors of 58 are those numbers that can be divided by 58 without leaving any remainder. This means that when 58 is divided by any of these factors, the remainder produced as a result is always equal to zero. If a zero remainder is not produced, then that specific number is not a factor of 58.
Figure 1 – All possible Factors of 58
What Are the Factors of 58?
The factors of 58 are the following: 1, 2, 29, and 58. Hence, it has four factors that will make two-factor pairs: (1, 58) and (2, 29).58 is an even number, meaning that two must be a factor because all even numbers are entirely divided by 2. This proves how just observing any number can provide valuable insights into it. Secondly, 58 is not a prime number, so it must have factors other than 1 and 58. This means that it will have more than two factors.How To Calculate the Factors of 58?
Using the division method, we find factors of 58 by dividing them by different numbers. The numbers which divide 58 ultimately, producing a zero remainder, are called the factors of 58.Before attempting to determine the factors of 58, it is better to calculate the range of these factors, so we do not have to keep dividing endlessly. This range can be calculated by using one as its initial point, and the final point of the range can be calculated using the formula:The final point of range = Given number / 2
Final point of range =$\dfrac{ 58}{ 2} $
The final point of range = 29
This shows that the range of factors for 58 other than 1 and 58 itself would be between 2 and 29.Once we have calculated the range, let us get to dividing the number:\[ \frac{58}{ 2} = 29 \]\[ \frac{58}{ 3} = 19.33 \]\[ \frac{58}{4} = 14.5 \]\[ \frac{58}{ 5} = 11.6 \]\[ \frac{58 }{ 7} = 8.2 \]\[ \frac{58}{ 10} = 5.8 \].
.
.
\[ \frac{58}{ 29 }= 2 \]\[ \frac{58 }{ 58} = 1 \]\[ \frac{58 }{1} = 58 \]The steps shown above represent that 58 is only divisible entirely by 2 and 29. Moreover, like all-natural numbers, it is divisible by 1 and 58. Therefore, the factors of 58 are:Factors of 58 through division method: 1, 2, 29, and 58Now the factors of any number can not only be positive, but they can also be negative. So 58 has both positive and negative factors. The negative factors of 58 are:Negative factors of 58 = -1, -2, -29, and -58Factors of 58 by Prime Factorization
In prime factorization of 58, it is divided into its prime factors. This means we get multiple prime factors upon performing prime factorization on 58. These prime factors multiply together to give 58. These prime factors can be calculated by dividing 58 by prime numbers. But this will not be a simple division like the division method, where we use a trial-based method to determine the factors by testing each number. We divide 58 by the smallest divisible prime number to obtain a quotient which must be a whole number. In the next step, we use this same quotient as the dividend. Now we select such a prime number that not only divides this quotient ultimately but must also be the smallest prime to do so. After this division, another quotient is obtained. We rinse and repeat as we did above.58 is our given number:58 $\div$ 2 = 29
2 is our smallest prime number, which we know can divide 58 completely as 58 is an even number. 29 is a whole number, meaning that 2 is a factor of 58 indeed.In the next step, we use 29 as our dividend:29 $\div$ 29 = 1
29 is a prime number and is only divisible by itself.The final answer is equal to 1. This means that we can not divide further and have obtained our prime factors.The prime factors of 58 are 2 and 29. The prime factorization method is represented using an equation shown below:The prime factorization of 58 = 2 x 29
We have calculated the prime factorization of 29 and shown the technique in Figure 2 attached below: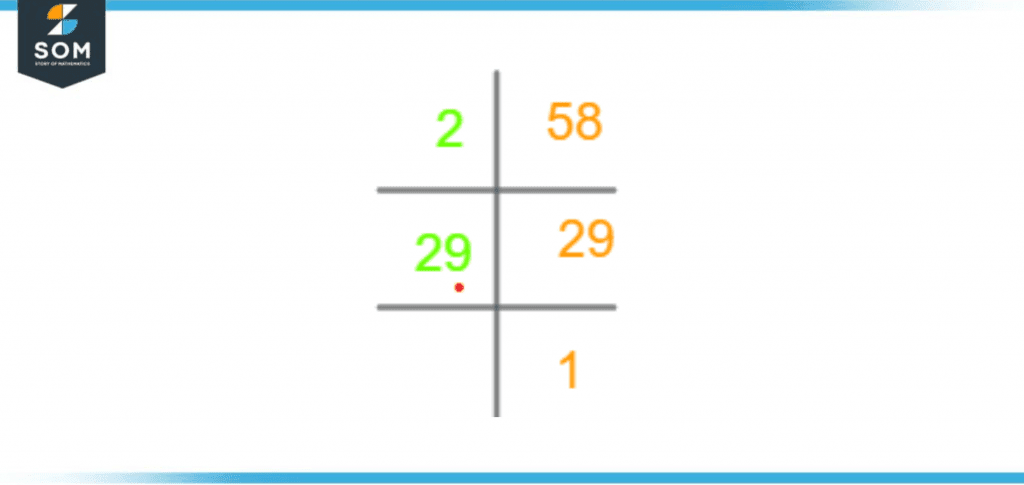
Figure 2 – Prime Factorization of 158
Factor Tree of 58
The factor tree of 58 is a schematic based on a tree used to represent any number’s factorization. The given number is written at the top of the tree while the factors, or to be more specific, the prime factors, are written at their roots or ends.The method begins by writing down the given number. After performing division with a prime factor, both quotient and divisor are noted down on each branch, coming out of 58. For the next step, we divide the quotient with a new prime factor. This is continued until we can not divide further. This stage is reached when we obtain prime numbers at all tree branches. Figure 3, shown below, has the diagram of the factor tree of 58 drawn using GeoGebra: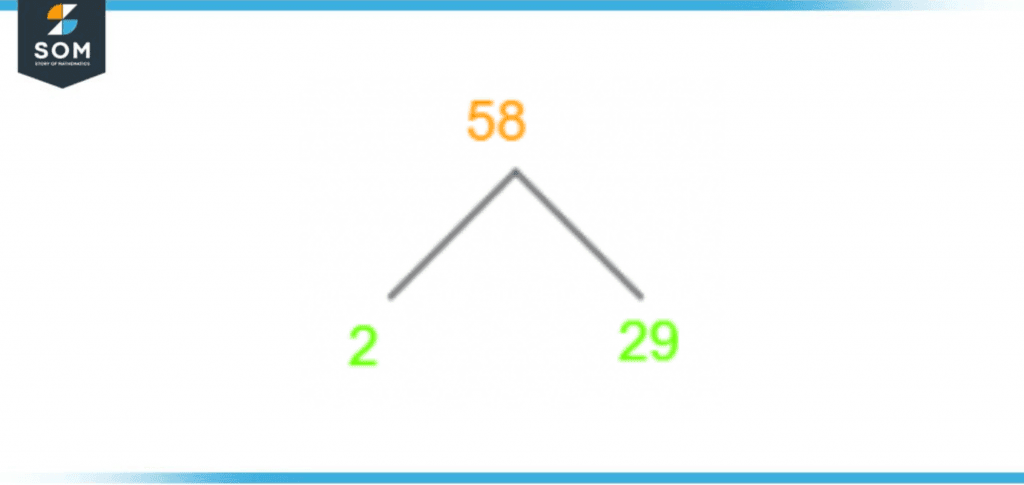
Figure 3 – Factor Tree of 58
Factors of 58 in Pairs
The factor pairs of 58 are pairs of numbers that will give 58 when multiplied by each other. If a pair of factors does not provide 58 upon multiplication, it is not a factor pair in mathematical terms. They can be both positive and negative depending on the sign attached to them.To find out the factor pairs, we need to look at the factors of 58. First, the factors of 58 are:Factors of 58 = 1, 2, 29, and 58Using these factors, we will find out the positive factor pairs of 58:1 x 2 = 2 (Not a factor pair because multiplication does not give 58)
1 x 29 = 29 (Not a factor pair because multiplication does not give 58)
1 x 58 = 58 (Factor pair because multiplication gives 58)
2 x 29 = 58 (Factor pair because multiplication gives 58)
2 x 58 = 116 (Not a factor pair because multiplication does not give 58)
29 x 58 = 1682 (Not a factor pair because multiplication does not give 58)
Working on the method above, we can reduce the pairs into the following factor pairs:Positive factor pairs of 58 = (1, 58), (2, 29)The negative factor pairs can be expressed using the same methodology, but we can introduce a negative sign with every number as we have already obtained the factor pairs.Multiplying two negatives give a positive so that we will introduce a negative sign with both numbers in a pair:Negative factor pairs of 58 = (-1, -58), (-2, -29)To verify, we can multiply them to check if they give 58 or not:-1 x -58 = 58
-2 x -29 = 58
We can see that both pairs give 58, so we have our positive and negative factors pairs of 58.Factors of 58 Solved Examples
We will deal with some solved examples in this section to further our comprehension of this topic.Example 1
Verify whether 58 is a factor of 116.Solution
To verify whether 58 is a factor of 116, we need first to find out the factors of 116. These factors can be calculated using the division method:\[ \frac{116}{ 2} = 58\] \[ \frac{116 }{ 4} = 29\]\[ \frac{116 }{58} = 2 \]\[ \frac{116}{ 29} = 4 \]\[ \frac{116 }{ 116} = 1 \]\[ \frac{116}{ 1} = 116 \]Factors of 116 = 1, 2, 4, 29, 58, and 116.Using the factor list of 116, we can verify whether 58 is a factor of 116 by checking if 58 exists in the factor of 116. The factors of 116 are 1, 2, 4, 29, 58, 116, and 58 is in this list. Hence, 58 is a factor of 116.Therefore, 58 is a factor of 116.Example 2
Calculate the average of the factors of 58.Solution
The factors of 58 can be calculated using the division technique. These factors are:Factors of 58 = 1, 2, 29, and 58.The average of these factors can be calculated using this formula:Average = Sum of all factors of 58/ number of factors of 58
Average =( 1 + 2 + 29 + 58) / 4
Average = 90 / 4
Average = 22.5
Therefore, the average of the factors of 58 is equal to 22.5.All images/mathematical drawings are created with GeoGebra.